Генерировать строения в майнкрафт что значит
Создаём свою Minecraft: генерация 3D-уровней из кубов
Частично из-за популярности Minecraft, в последнее время наблюдается рост интереса к идее игры, действие которой происходит в состоящем из кубов мире, построенном из 3D-рельефа и заполненного такими элементами, как пещеры, обрывы и так далее. Такой мир — идеальное применение для шума, сгенерированного в стиле моей библиотеки ANL. Данная статья возникла из обсуждений моих предыдущих попыток реализации этой техники. С тех пор в структуре библиотеки появились незначительные изменения.
В предыдущих постах я рассказывал об использовании функций 3D-шума для реализации рельефа в стиле Minecraft. После этого библиотека немного эволюционировала, поэтому я решил вернуться к этой теме. Так как мне пришлось отвечать на множество вопросов по этой системе, я попытаюсь более подробно рассказать о задействованных концепциях. Чтобы базовые концепции были понятнее, я начну с идеи генерации 2D-рельефа, используемого в таких играх, как Terraria и King Arthur’s Gold, а затем расширю систему до 3D-примеров наподобие Minecraft. Это позволит мне эффективнее демонстрировать концепции на примере изображений.
Эта система разрабатывалась с учётом следующей абстрактной цели: мы должны иметь возможность передать системе координату определённой точки или ячейки, и определить, какой тип блока должен находиться в этой локации. Мы хотим, чтобы система представляла собой «чёрный ящик»: передаём ей точку, возвращаем тип блока. Разумеется, это относится только к изначальной генерации мира. Блоки в подобных играх могут изменяться действиями игрока, и будет неудобно пытаться описать такие изменения при помощи такой же системы. Подобные изменения должны отслеживаться каким-то иным образом. Эта система генерирует изначальный мир, первозданный и нетронутый руками игрока и других персонажей.
Возможно, эта техника не подойдёт для моделирования таких систем, как трава или другие биологические сущности, учитывая то, что такие системы сами по себе являются сложными сущностями, которые не так легко моделировать неявным образом. То же самое относится к таким системам, как падающий снег, образование льда и т.д… Описанная в статье техника представляет собой неявный метод, т.е. такой, который может быть оценен в точке, и значение которого в заданной точке не зависит от окружающих значений. Биологические и другие типы систем для выполнения точной симуляции обычно должны учитывать окружающие значения. Например: сколько солнечного света падает на блок? Есть ли поблизости вода? На эти и другие вопросы нужно ответить для симуляции роста и распространения биологических систем, а также, в меньшей степени, других типов связанных с климатом систем. Также эта техника не подходит для моделирования воды. В этой системе отсутствует понятие потока, знание о механике жидкости или гравитации. Вода — это сложная тема, требующая множества сложных вычислений.
(Вкратце объясню запись. Код примеров записан в виде таблицы объявлений Lua. Подробнее о формате можно прочитать в разделе про интеграции с Lua. По сути, формат предназначен для парсинга специальным классом, считывающим объявления и превращающим их в деревья экземпляров модулей шума. Я предпочитаю этот формат более многословному пошаговому формату C++, потому что компактнее и чище. По-моему, исходный код получается более читаемым и сжатым, чем код на C++. По большей части объявления легко читаемы и понятны. Модули имеют названия, источники заданы именем или значением. Код на Lua, используемый для парсинга объявления таблицы, включён в исходники на случай, если вы захотите использовать эти объявления напрямую.)
В случае 2D функция Gradient получает отрезок прямой в виде (x1,x2, y1,y2), а в случае 3D формат расширен до (x1,x2, y1,y2, z1,z2). Точка, образованная (x1,y1), обозначает начало отрезка прямой, сопоставленное с 0. Точка, образованная (x2,y2) — это конец отрезка, сопоставленный с 1. То есть здесь мы сопоставляем отрезок прямой (0,1)->(0,0) с градиентом. Следовательно, градиент будет находиться между областями функции Y=1 и Y=0. То есть эта полоса образует размеры мира по Y. Любая часть мира будет находиться в этой полосе. Мы можем привязать любой регион по X (практически до бесконечности, но здесь нас ограничивает точность double ), но всё интересное, т.е. поверхность земли, будет находиться в пределах этой полосы. Такое поведение можно изменить, но и в его пределах мы имеем большую степень гибкости. Просто не забывайте, что любые значения, которые находятся над или под этой полосой, скорее всего будут не интересными, потому что значения выше вероятнее всего будут воздухом, а значения ниже — землёй. (Как вы вскоре увидите, это заявление вполне может оказаться ошибочным.) Для большинства изображений в этой серии я буду сопоставлять квадратный регион, заданный квадратом (0,1)->(1,0) в 2D пространстве. Следовательно, в начале наш мир выглядит так:
Пока ничего интересного; к тому же, это изображение не отвечает на вопрос «заданная точка сплошная или полая?». Чтобы ответить на этот вопрос, нам нужно применить Step Function (кусочно-заданную функцию). Вместо плавного градиента нам нужно чёткое разделение, при котором все локации с одной стороны полые, а все локации с другой стороны — сплошные. В ANL это можно реализовать при помощи функции Select. Функция Select получает две входящие функции или значения (в этом случае они будут равны «сплошному» (Solid) и «полому» (Open)), и выбирает из них на основании значения контрольной функции (в данном случае Gradient). Модуль Select имеет два дополнительных параметра, threshold и falloff, которые влияют на этот процесс. На данном этапе falloff нежелателен, поэтому мы сделаем его равным 0. Параметр threshold решает, где будет проходить разделительная линия между Solid и Open. Всё, что в функции Gradient будет больше этого значения, превратится в Solid, а всё, что меньше порога — в Open. Так как Gradient сопоставляет интервал со значениями от 0 и 1, логично будет расположить порог в 0.5. Так мы разделим пространство ровно пополам. Значение 1 будет сплошной локацией, а значение 0 — полой. То есть мы зададим функцию плоскости земли следующим образом:
Сопоставив ту же область функции, что и раньше, мы получим нечто подобное:
Такая картина чётко отвечает на вопрос, является ли заданная точка сплошной или полой. Мы можем вызвать функцию с любой возможной координатой 2D-пространства, и её результат будет равен или 1, или 0, в зависимости от того, где находится точка относительно поверхности земли. Тем не менее, такая функция не особо интересна, это всего лишь плоская линия, протянувшаяся в бесконечность. Чтобы оживить картину, мы используем технику под названием «турбулентность» («turbulence»).
«Турбулентность» — это сложное обозначение концепции добавления значений к входящим координатам функции. Представьте, что мы вызываем показанную выше функцию земли с координатой (0,1). Она лежит над плоскостью земли, потому что при Y=1 градиент имеет значене 0, что меньше threshold = 0.5. То есть эта точка будет вычислена как Open. Но что если перед вызовом функции земли мы каким-то образом преобразуем эту точку? Допустим, вычтем из координаты Y случайное значение, например, 3. Мы вычитаем 3 и получаем координату (0,-2). Если теперь мы вызовем функцию земли для этой точки, то точка будет считаться сплошной, потому что Y=-2 лежит ниже сегмента Gradient, соответствующего 1. Внезапно полая точка (0,1) превращается в сплошную. У нас получится висящий в воздухе блок сплошного камня. Так можно сделать с любой точкой в функции, прибавляя или вычитая случайное число из координаты Y входящей точки до вызова функции ground_select. Вот изображение функции ground_select, показывающее это. Перед вызовом функции ground_select к координате Y каждой точки прибавляется значение в интервале (-0.25, 0.25).
Это уже интереснее, чем плоская линия, но не очень похоже на землю, потому что каждая точка перемещается на совершенно случайное значение, что создаёт хаотичный паттерн. Однако если мы используем непрерывную случайную функцию, например, Fractal из библиотеки ANL, то вместо беспорядочного паттерна получим нечто более управляемое. Поэтому давайте подключим к плоскости земли фрактал и посмотрим, что получится.
Здесь стоит заметить пару аспектов. Во-первых, мы задаём модуль Fractal, и соединяем его цепочкой с модулем ScaleOffset. Модуль ScaleOffset масштабирует выходные значения фрактала до более удобного уровня. Часть рельефа может быть горной и требовать большего масштаба, а другая часть — более плоской и с меньшим масштабом. О разных типах рельефа мы поговорим позже, а пока используем их для демонстрации. Выходные значения функции теперь дадут такую картину:
Это уже интереснее, чем просто случайный шум, правда? По крайней мере, больше похоже на землю, хотя часть ландшафта выглядит необычно, а летающие острова и вовсе странно. Причиной этого стало то, что каждая отдельная точка выходной карты случайным образом смещена на разное значение, определяемое фракталом. Чтобы проиллюстрировать это, покажем выходные данные фрактала, выполняющие искажение:
Мы хотим заставить функцию вести себя подобно функции карты высот. Представьте 2D-карту высот, где каждая точка карты обозначает высоту точки в решётке точек сетки, которые подняты вверх или опущены вниз. Белые значения карты обозначают высокие холмы, чёрные — низкие долины. Нам нужно похожее поведение, но чтобы добиться его, нужно по сути избавиться от одного из измерений. В случае карты высот мы создаём 3D-рельеф из 2D-карты высот. Аналогично, в случае 2D-рельефа нам нужна 1D-карта высот. Сделав так, чтобы все точки фрактала с одинаковой координатой Y имели одинаковое значение, мы можем сместить все точки с одинаковой координатой X на одинаковую величину, благодаря чему летающие острова исчезнут. Для этого можно использовать ScaleDomain, обнулив коэффициент scaley. То есть перед вызовом функции ground_shape_fractal мы вызываем ground_scale_y, чтобы присвоить координате y значение 0. Это гарантирует, что значение Y не будет влиять на выходные данные фрактала, по сути превратив его в функцию 1D-шума. Для этого мы внесём следующие изменения:
Мы соединим функцию ScaleDomain в цепочку с ground_scale, а затем изменим исходные данные ground_perturb, чтобы они были функцией ScaleDomain. Это изменит фрактал, смещающий землю и превратит его в нечто подобное:
Теперь если мы взглянем на выходные данные, то получим результат:
Намного лучше. Летающие острова полностью исчезли, а рельеф больше напоминает горы и холмы. К сожалению, при этом мы потеряли выступы и обрывы. Теперь вся земля непрерывная и покатая. При желании можно исправить это несколькими способами.
Во-первых, можно использовать ещё одну функцию TranslateDomain, соединённую с ещё одной функцией Fractal. Если мы применим к направлению по X небольшую величину фрактальной турбулентности, то сможем немного исказить края и поверхности гор, и этого возможно будет достаточно для образования обрывов и выступов. Давайте посмотрим на это в действии.
Второй способ: можно просто присвоить параметру scaley функции ground_scale_y значение больше 0. Если оставить небольшой масштаб по Y, то мы получим долю вариативности, однако чем больше будет масштаб, тем сильнее рельеф будет напоминать прежнюю версию без масштабирования.
Результаты выглядят намного интереснее, чем обычные покатые горы. Однако как бы ни интересны они были, игроку всё равно наскучит исследовать рельеф с одинаковым паттерном, растянувшийся на многие километры. Кроме того, такой рельеф будет очень нереалистичным. В реальном мире есть большая вариативность, повышающая интересность рельефа. Давайте посмотрим, что можно сделать, чтобы мир стало более разнообразным.
Взглянув на предыдущий пример кода, можно увидеть в нём определённый паттерн. У нас есть функция градиента, которая управляется функциями, придающими земле форму, после чего применяется кусочно-заданная функция и земля обретает заполненность. То есть усложнять рельеф логичнее будет на этапе придания земле формы. Вместо одного фрактала, смещающего по Y и другого, смещающего по X, мы можем добиться нужной степени сложности (с учётом производительности: каждый фрактал требует дополнительных вычислительных затрат, поэтому надо стараться быть консервативными.) Мы можем задать формы земли, представляющие собой горы, предгорья, плоские низины, пустоши, и т.д… и использовать выходные данные различных функций Select, объединённых в цепочки с низкочастотными фракталами, чтобы очертить области каждого типа. Итак, давайте посмотрим, как можно реализовать разные типы рельефа.
Чтобы проиллюстрировать принцип, мы выделим три типа рельефа: плоскогорья (плавные покатые холмы), горы и низины (по больше части плоские). Для переключения между ними мы используем систему на основе select и соединим их в сложное полотно. Итак, начинаем…
С ними всё просто. Мы можем взять использованную выше схему, немного снизить амплитуду холмов, возможно, даже сделать их более субтрактивными, чем аддитивными. чтобы опустить средние высоты. Также мы можем снизить количество октав, чтобы сгладить их.
С ними тоже всё просто. (На самом деле, ни один из этих типов рельефа не представляет трудностей.) Однако мы используем другой базис, чтобы сделать холмы похожими на дюны.
Разумеется, можно подойти к этому процессу ещё более творчески, но в целом паттерн будет таким. Мы выделяем характеристики типа рельефа и подбираем под них функции шума. Для всего этого действуют одинаковые принципы; основные различия заключаются масштабе. Теперь чтобы соединить их вместе, мы подготовим дополнительные фракталы, которые будут управлять функцией Select. Затем мы объединим в цепочку модули Select для генерации всего рельефа.
Итак, здесь мы задаём три основных типа рельефа: lowlands, highlands и mountains. Используем один фрактал для выбора одного из них, чтобы присутствовали естественные переходы (lowlands->highlands->mountains). Затем используем ещё один фрактал для случайной вставки в карту пустошей (badlands). Вот как выглядит готовая цепочка модулей:
Вот несколько примеров получаемых рельефов:
Можно заметить, что получается достаточно высокая вариативность. В некоторых местах появляются возвышающиеся изломанные горы, в других есть плавные покатые равнины. Теперь нам нужно добавить пещеры, чтобы можно было исследовать чудеса подземного мира.
Для пещер я использую мультипликативную систему, применяемую к ground_select. То есть я создаю функцию, выводящую 1 или 0, и умножаю их на выходные данные ground_select. Благодаря этому полой становится любая точка функции, для которой значение функции пещер равно 0. То есть там, где я захочу получить пещеру, функция пещер должна возвратить 0, а там, где пещеры быть не должно, функция должна быть равна 1. Что касается формы пещер, я хочу основать систему пещер на основе 1-октавного Ridged Multifractal.
В результате получится нечто такое:
Если применить функцию Select как кусочно-заданную функцию, как мы делали с градиентом земли, реализовав её так, чтобы нижняя часть порога select была равна 1 (нет пещеры), а верхняя часть равна 0 (есть пещера), то результат будет примерно выглядеть так:
Конечно, он выглядит довольно плавным, поэтому добавим немного фрактального шума, чтобы исказить область.
Это слегка зашумливает пещеры и делает их не такими плавными. Давайте теперь посмотрим, что произойдёт, если применить пещеры к рельефу:
Поэкспериментировав со значением threshold в cave_select, мы можем делать пещеры тоньше или толще. Но главное, что нам нужно попробовать — сделать так, чтобы пещеры не отъедали такие огромные фрагменты поверхностного рельефа. Для этого можно вернутся к функции highland_lowland_select, которая, как мы помним, является последней функцией рельефа, искажающей градиент земли. В этой функции полезно то, что она всё ещё является градиентом, увеличивающим значение при углублении функции в землю. Мы можем использовать градиент для ослабления функции пещер, чтобы пещеры увеличивались при углублении в землю. К счастью для нас, это ослабление можно реализовать просто умножением выходных данных функции highland_lowland_select на выходные данные cave_shape, а затем передать результат остальной цепочке функций. Далее мы внесём здесь важное изменение — добавим функцию Cache. Функция кэширования сохраняет результат функции для заданной входящей координаты, и если функция вызывается повторно с той же координатой, она вернёт кэшированную копию, а не будет вычислять результат повторно. Это полезно в подобных ситуациях, когда одна сложная функция (highland_lowland_select) в цепочке функций вызывается несколько раз. Без кэша вся цепочка сложной функции при каждом вызове вычисляется заново. Чтобы добавить кэш, нам сначала нужно внести следующие изменения:
Так мы добавили Cache, а затем перенаправили входные данные ground_select, чтобы они брались из кэша, а не напрямую из функции. Затем мы можем изменить код пещер, чтобы добавить ослабление:
Первым делом мы добавили функцию Bias. Это сделано ради удобства, потому что позволяет нам настраивать интервал функции ослабления градиента. Затем добавлена функция cave_shape_attenuate, которая является Combiner типа anl::MULT. Она умножает градиент на cave_shape. Затем результат этой операции передаётся функции cave_perturb. Результат выглядит примерно так:
Мы видим, что ближе к поверхности земли стали тоньше. (Не обращайте внимание на самый верх, это просто артефакт отрицательных значений градиента, он не влияет на готовые пещеры. Если это станет проблемой — допустим, если мы используем эту функцию для чего-то другого, то перед использованием градиент можно ограничить интервалом (0,1).) Немного трудно увидеть, как это работает в отношении к рельефу, поэтому давайте двинемся дальше и соединим всё вместе, чтобы посмотреть, что получится. Вот вся цепочка функций, которую мы пока создали.
Вот примеры рандомизированных карт, полученных из этой функции:
Теперь всё выглядит довольно неплохо. Все пещеры представляют собой довольно большие каверны глубоко под землёй, но ближе к поверхности они обычно превращаются в маленькие туннели. Это помогает создать атмосферу загадочности. Исследуя поверхность, вы обнаруживаете небольшой вход в пещеру. Куда она ведёт? Насколько глубоко простирается? Мы не можем этого знать, но в процессе изучения она начинает расширяться, превращаясь в обширную систему каверн, заполненных тьмой и опасностями. И лутом, конечно. Там всегда много лута.
Можно изменять эту систему множеством разных способов, получая различные результаты. Мы можем изменять параметры threshold для cave_select и параметры у cave_attenuate_bias, или заменять cave_attenuate_bias на другие функции, чтобы сопоставлять интервал градиента с иными значениями, лучше подходящими вашим потребностям. Также можно добавить ещё один фрактал, искажающий систему пещер по оси Y, чтобы устранить возможность появления неестественно плавных туннелей по оси X (вызванных тем, что форма пещер искажается только по X). Ещё можно добавить новый фрактал как дополнительный источник ослабления, задать третий источник для cave_shape_attenuate, масштабирующий ослабление на основе регионов, чтобы пещеры в некоторых областях располагались плотнее (допустим, в горах), а в других реже или вовсе отсутствовали. Этот региональный select можно создать из функции terrain_type_fractal, чтобы знать, где расположены области гор. Всё сводится просто к тому, чтобы продумать, чего вы хотите, разобраться в том, какое влияние разные функции будут оказывать на выходные данные, и поэкспериментировать с параметрами, пока не получите нужный результат. Это не точная наука, и часто к нужному эффекту можно прийти разными путями.
Недостатки
У этого метода генерации рельефа есть недостатки. Процесс генерации шума может быть довольно медленным. Важно по возможности уменьшать количество фракталов, количество октав тех фракталов, которые вы используете, и других медленных операций. Пытайтесь использовать фракталы многократно и кэшировать все функции, которые вызываются несколько раз. В этом примере я достаточно вольно пользовался фракталами, создав по одному для каждого из трёх типов рельефа. Воспользовавшись ScaleOffset для изменения интервалов и взяв за основу для них всех один фрактал, я бы сэкономил много процессорного времени. В 2D всё не так плохо, но когда вы доберётесь до 3D и попробуете сопоставлять объёмы данных, время обработки сильно увеличится.
Переходим в 3D
Всё это здорово, если вы создаёте игру наподобие Terraria или King Arthur’s Gold, но что, если вам нужно нечто наподобие Minecraft или Infiniminer? Какие изменения нам нужно будет внести в цепочку функций? На самом деле, их не так много. Показанная выше функция почти без модификаций сработает и для 3D-рельефа. Вам достаточно будет сопоставить 3D-объём, используя 3D-вариации генератора, а также сопоставить ось Y с вертикальной осью объёма, а не 2D-областью. Однако всё-таки потребуется одно изменение, а именно, способ реализации пещер. Как вы видели, Ridged Multifractal отлично подходит для 2D-системы пещер, но в 3D он вырезает множество искривлённых оболочек, а не туннелей, и его влияние оказывается неверным. То есть в 3D необходимо задать два фрактала форм пещер, оба являются 1-октавным шумом Ridged Multifractal, но с разными seed. При помощи Select задаём им значения 1 или 0, и перемножаем их. Таким образом, в местах пересечения фракталов появится пещера, а всё остальное останется сплошным, и внешний вид туннелей станет более естественным, чем при использовании одного фрактала.
Генерация карты
Шкала генерации и загрузки мира
Генерация карты — это процесс случайного создания географических и геологических объектов на карте при первом запуске игры на пустом слоте для игрового мира. Процесс генерации отображается на шкале, которую можно увидеть при первой генерации карты. Но при этом карта генерируется не до конца. Она будет продолжать генерироваться по мере продвижения вами по карте. Это сделано для того, чтобы не нагружать игру и компьютер генерацией при первом запуске.
Алгоритм генерации [ ]
Алгоритм генерации несколько раз изменялся. Теперь ландшафт генерируется, хранится и загружается с диска и обрисовывается кусками по 16×16×16 блоков. У каждого куска имеется значение смещения, которое хранится в виде 32-битного целого числа и может находиться в диапазоне примерно от минус двух миллиардов до плюс двух миллиардов. Однако мир ограничен и генерируется только в координатах блоков до 30 миллионов во все стороны. Раньше этого ограничения не было и можно было выйти за пределы первого диапазона (а это примерно четверть расстояния от Земли до Солнца), тогда новые куски начинали перекрывать собой старые (так называемые «Далёкие земли»). А после того, как преодолена шестнадцатая часть этого расстояния, функции, использующие вещественные числа для работы с позициями блоков, такие как использование инструментов и поиск путей, начнут странно себя вести.
Генерация местности происходит в следующие несколько этапов:
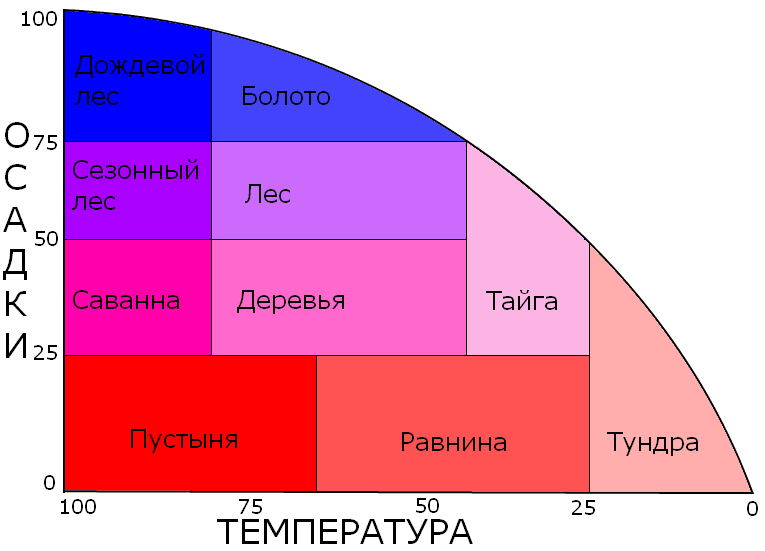
Генерация биомов [ ]
Примерный график генерации биомов
Это визуализация простого двумерного шума Перлина.
С помощью шума Перлина создаются карты температуры и влажности.
Также на температуру влияет высота. Исключая болото, через каждый блок над уровнем моря (y = 64) температура становится ниже на 1/600. Температура влияет не только на карту биомов, но и на наличие осадков (За исключением грозы, возникающей в любых биомах Верхнего мира). На частоту выпадения осадков влияет влажность. В зависимости от температуры и влажности генерируется карта биомов. Биом реки генерируется на стыке двух биомов или с некоторым шансом в пределе одного биома.
Генерация ландшафта [ ]
В ранних версиях игры для придания миру формы была использована карта высот на основе двумерного шума Перлина. Или, если быть точнее, несколько карт высот. Одна для общей высоты, одна для шероховатости ландшафта и одна для мелких деталей. Для каждого столба блоков высота равнялась (общая высота + (шероховатость×детали))×64+64. Карты общей высоты и шероховатости были гладкими, сильно масштабированными шумами, а детали были более мелкими. У этого метода было замечательное преимущество в скорости, так как нужно было проводить всего 16×16×(количество_шумов) расчетов на чанк, но его недостатком был скучный ландшафт. В частности из-за невозможности генерировать нависающие над землей выступы.
С версии Beta 1.3 игра перешла на похожую систему, использующую трёхмерный шум Перлина. Теперь уже не генерируется «высота земли». Значение шума было рассматривается как «плотность», и все блоки с плотностью меньше 0 становятся воздухом, а блоки с плотностью больше или равной 0 — землёй. Чтобы нижний слой был твёрдый, а верхний — нет, к полученному результату прибавляется высота (смещение относительно уровня моря).
К сожалению, мгновенно появились проблемы производительности и играбельности. Первые — из-за большого количества требуемых расчетов, вторые — из-за отсутствия плоских местностей и гладких холмов. Решение обеих проблем заключалось в понижении разрешения при расчетах (8x масштабирование по горизонталям и 4x по вертикали) и достраивании ландшафта с помощью линейной интерполяции. В игре появились плоскости и холмы, а заодно исчезло большинство парящих в воздухе блоков.
Окончательная формула, которая используется сейчас, сильно улучшена. Она медленно развивалась в течение разработки игры, и, кстати, до сих пор использует двумерные шумы.






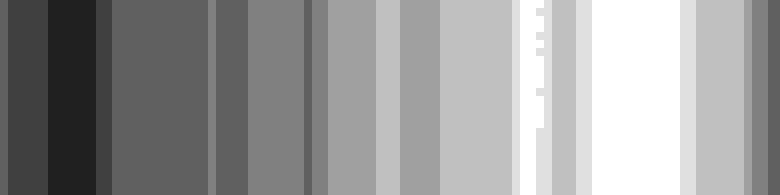













_%D0%BC%D0%B8%D1%80%D0%B0.png)