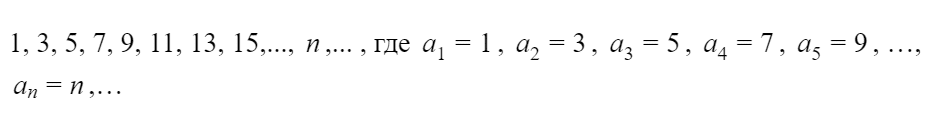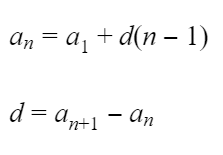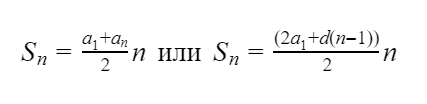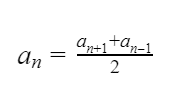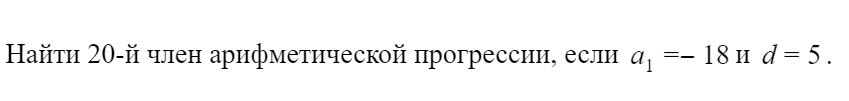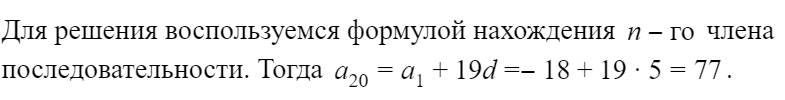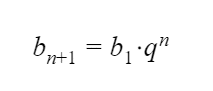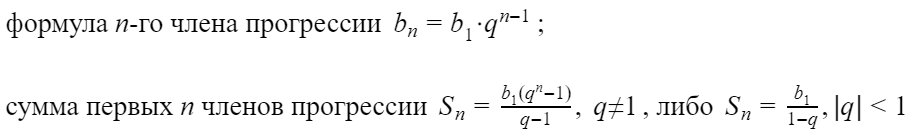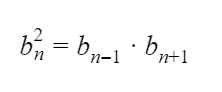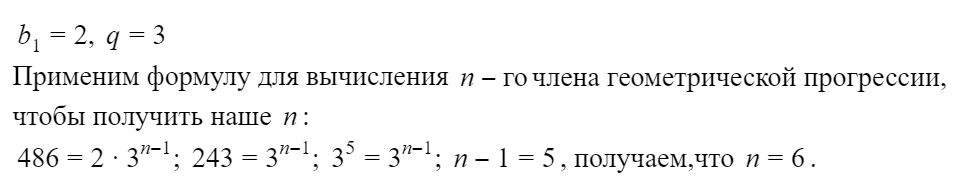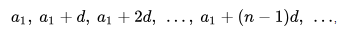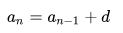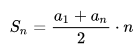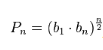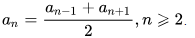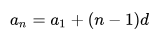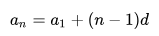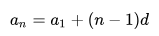Геометрическая прогрессия и арифметическая чем отличаются
math4school.ru
Арифметическая и геометрическая прогрессии
Числовые последовательности (основные понятия)
Если каждому натуральному числу n поставить в соответствие действительное число an , то говорят, что задано числовую последовательность :
Итак, числовая последовательность — функция натурального аргумента.
Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.
последовательность положительных нечётных чисел можно задать формулой
а последовательность чередующихся 1 и –1 — формулой
Последовательность можно определить рекуррентной формулой, то есть формулой, которая выражает любой член последовательности, начиная с некоторого, через предыдущие (один или несколько) члены.
последовательность двузначных натуральных чисел:
Последовательность простых чисел:
Монотонными последовательностями, в частности, являются возрастающие последовательности и убывающие последовательности.
Арифметическая прогрессия
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, к которому прибавляется одно и то же число.
является арифметической прогрессией, если для любого натурального числа n выполняется условие:
где d — некоторое число.
Таким образом, разность между последующим и предыдущим членами данной арифметической прогрессии всегда постоянна:
Чтобы задать арифметическую прогрессию, достаточно указать её первый член и разность.
найдём тридцатый член арифметической прогрессии
| an = | an–1 + an+1 |
| 2 |
каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.
Так как верно и обратное утверждение, то имеет место следующее утверждение:
числа a, b и c являются последовательными членами некоторой арифметической прогрессии тогда и только тогда, когда одно из них равно среднему арифметическому двух других.
Воспользуемся приведённым выше утверждением. Имеем:
| an+1 + an–1 | = | 2n – 5 + 2n – 9 | = 2n – 7 = an, |
| 2 | 2 |
что и доказывает нужное утверждение. ◄
| an = | a n–k + a n+k |
| 2 |
любой член арифметической прогрессии, начиная со второго равен полусумме равноотстоящих от него членов этой арифметической прогрессии.
Кроме того, для любой арифметической прогрессии справедливо равенство:
первых n членов арифметической прогрессии равна произведению полусуммы крайних слагаемых на число слагаемых:
Отсюда, в частности, следует, что если нужно просуммировать члены
то предыдущая формула сохраняет свою структуру:
Если дана арифметическая прогрессия, то величины a1, an, d, n и S n связаны двумя формулами:
| an = a1 + (n – 1)d и Sn = | a1 + an | · n . |
| 2 |
Поэтому, если значения трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.
Арифметическая прогрессия является монотонной последовательностью. При этом:
Геометрическая прогрессия
Геометрической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
является геометрической прогрессией, если для любого натурального числа n выполняется условие:
где q ≠ 0 — некоторое число.
Таким образом, отношение последующего члена данной геометрической прогрессии к предыдущему есть число постоянное:
Чтобы задать геометрическую прогрессию, достаточно указать её первый член и знаменатель.
каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому (пропорциональному) предшествующего и последующего членов.
Так как верно и обратное утверждение, то имеет место следующее утверждение:
числа a, b и c являются последовательными членами некоторой геометрической прогрессии тогда и только тогда, когда квадрат одного из них равен произведению двух других, то есть одно из чисел является средним геометрическим двух других.
что и доказывает нужное утверждение. ◄
квадрат любого члена геометрической прогрессии, начиная со второго равен произведению равноотстоящих от него членов этой прогрессии.
Кроме того, для любой геометрической прогрессии справедливо равенство:
первых n членов геометрической прогрессии со знаменателем q ≠ 0 вычисляется по формуле:
| Sn = b1 · | 1 – q n | . |
| 1 – q |
А при q = 1 — по формуле
Заметим, что если нужно просуммировать члены
то используется формула:
Если дана геометрическая прогрессия, то величины b1, bn, q, n и Sn связаны двумя формулами:
| bn = b1 · q n –1 и Sn = b1 · | 1 – q n | . |
| 1 – q |
Поэтому, если значения каких-либо трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.
Для геометрической прогрессии с первым членом b1 и знаменателем q имеют место следующие свойства монотонности :
Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
Бесконечно убывающая геометрическая прогрессия
Заметим, что бесконечно убывающая геометрическая прогрессия может не быть убывающей последовательностью. Это соответствует случаю
При таком знаменателе последовательность знакопеременная. Например,
Связь арифметической и геометрической прогрессий
Арифметическая и геометрическая прогрессии тесно связаны между собой. Рассмотрим лишь два примера.
Арифметическая и геометрическая прогрессии.
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Арифметическая прогрессия Арифметическая прогрессия – это числовая последовательность вида: a, a+d, a+2d, a+3d… И вычисляется по формуле: an=a1+d(n-1). d=a2-a1
Сравнение прогрессий Арифметическая прогрессии: Примеры: 3, 5, 7, 9… a1=3, a2=5, a3=7 и т.д. d=2 Геометрическая прогрессия: Примеры: 3, 6, 12, 24… b1=3, b2=6, b3=12 и т.д. q=2 an=a1+d(n-1) d=a2-a1
Таким образом прогрессии отличаются лишь тем, что в арифметической прогрессии числа складываются или вычитаются на одно и тоже число, а в геометрической прогрессии числа умножаются на одно и тоже число.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДВ-382371
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Апробацию новых учебников по ОБЖ завершат к середине 2022 года
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Школьников Улан-Удэ перевели на удаленку из-за гриппа и ОРВИ
Время чтения: 1 минута
Костромская область разработала программу привлечения педагогических кадров
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Прогрессии и последовательности: решаем ОГЭ по математике
Григорий Грянников
Тема «прогрессии» на ОГЭ тесно связана с понятием «последовательность». Если ученики понимают, как числа в последовательности связаны друг с другом, они легко справляются с заданиями. Сейчас мы разберем прогрессии — одну из самых коварных тем ОГЭ по математике. Обратите внимание: в этом материале все самое главное для решения ОГЭ, никакой воды!
Что такое последовательность?
В жизни мы очень часто сталкиваемся с математическими последовательностями и прогрессиями, буквально, каждый день, сами того не замечая. Однако встреча не всегда может быть приятной, особенно если она происходит на экзамене.
Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:
Хочешь круто подготовится к ОГЭ? Тебе поможет учебный центр MAXIMUM! Все наши преподаватели сами сдавали этот экзамен на хороший балл. Мы ежегодно изучаем изменения ФИПИ и корректируем курсы, исходя из этого. Читай подробнее про наши курсы и выбирай подходящий!
Какие виды последовательности бывают?
Различают следующие виды последовательности:
Что такое арифметическая прогрессия?
Давайте посмотрим на следующий ряд чисел:
Что же у них может быть общего? Во-первых, все они нечетные, во-вторых, каждое следующее число мы можем получить из предыдущего, прибавляя к нему одно и то же число. Назовем это число d. В нашем случае d=2.
Описанная выше последовательность называется арифметической прогрессией. Получаем определение:
Приведем основные формулы:
Сумма первых n членов прогрессии можно вычислить по формуле:
Также арифметическая прогрессия обладает характерным свойством:
Как решать задачи ОГЭ на арифметическую прогрессию?
Теория — это прекрасно, но каждую теоретическую тему необходимо закреплять на практике. Сейчас мы разберем пару заданий ОГЭ по арифметической прогрессии.
Например, на ОГЭ может попасться вот такое задание:
Решение:
Ура! Первый прототип задания, который может встретиться на реальном экзамене, успешно выполнен. Идем дальше.
Решение:
Вот и все! Ничего сложного, учитывая то, что формула суммы первых n членов прогрессии есть в справочных материалах, которые выдаются на экзамене.
Что такое геометрическая прогрессия?
Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии можно задать соотношением:
Вот основные формулы для геометрической прогрессии:
Также геометрическая прогрессия, как и арифметическая, обладает характерным свойством:
Как решать задачи ОГЭ на геометрическую прогрессию?
Закрепим материал на практике и разберем две задачи ОГЭ по геометрической прогрессии.
Как видите, со знанием формул любое задание становится несложным!
В каком задании ОГЭ могут встретиться прогрессии?
Тема «Прогрессия» встречается в задании ОГЭ под номером 12. Выполнение этого задания экзаменуемым зависит от уровня сложности самого задания. В среднем с ним справляется всего 47% школьников. Как видите, сама тема не очень сложная. Все можно решить — достаточно правильно и хорошо подготовиться.
Напомним, что в КИМах с инструкцией и заданиями есть вспомогательные формулы, которые помогут при решении нашей задачи на прогрессию.
Теперь вы знаете теорию по теме прогрессии на ОГЭ. Можете смело оттачивать знания на практике. Пусть ваша встреча с прогрессиями на экзамене будет не печальной, а победной!
Хотите разобраться в других темах ОГЭ? Боитесь, что экзамены уже в следующем году, а вы даже не открывали учебники? Начните готовиться к ОГЭ-2021 уже сейчас на курсах с MAXIMUM. Мы поможем закрыть пробелы и сдать все на отлично. Правильная и интересная подготовка — залог успеха на экзаменах. Консультация бесплатно!
Арифметическая (алгебраическая) прогрессия определение, примеры нахождения с решением
Часто, при решении задач, связанных с наблюдениями и присвоением значения определенному событию за определенный промежуток времени, получается ряд чисел, который именуется арифметической прогрессией.
Одна из главных отличительных особенностей такая математическая модель имеет закономерность, по которой можно вычислить любой неизвестный член, что упрощает прогнозирование при вычислении физических ситуаций.
Примерами повседневного использования могут являться наблюдение за температурой воздуха, прогнозирование расходов с занесением результатов в таблицу и др.
Онлайн-калькулятор арифметической прогрессии
Определение и примеры арифметической прогрессии
Это последовательность из чисел, где каждое последующее число ряда (начиная со второго) увеличивается или уменьшается на определенную сумму, являющуюся константой.
Кроме этого для описания используется ряд сопутствующих терминов и определений. Членом (аn) называется единичное число из последовательности.
Разностью (d) называется фиксированное число, на которое увеличивается или уменьшается последующее число прогрессии.
Кроме этого, существуют виды таких рядов:
В качестве примера представим последовательность чисел «3, 9, 15, 21, 27». Данный случай – этот ряд чисел попадает под характеристику арифметической прогрессии. Этот вывод делается в том случае, когда разница между членами ряда фиксирована и равняется 6.
Виды арифметической (алгебраической) прогрессии
Разновидности строятся на основании характеристики разности (d), а именно на основании отличия последней от нуля.
Таким образом, можно встретить определенные вариации:
Если прогрессия не изменяется с каждым шагом на одну и ту же разность, то эта прогрессия непостоянная и арифметической не является.
Важно знать: арифметическая от геометрической отличается тем, что в последней производится увеличение каждого последующего на один и тот же множитель.
Формулы арифметической прогрессии
Одно из важнейших свойств заключается в возможности вычисления любого числа конкретного места ряда.
Чтобы решать это, необходима формула, показывающая, как находится член арифметической прогрессии. В общем виде она будет выглядеть, как значение предыдущего числа в ряду (an-1), к которому прибавляют разность (d):
Также может возникнуть задача, когда надо просуммировать все числа ряда арифметической прогрессии (сумма членов). Если их малое количество, то можно посчитать это вручную, но если количество чисел перевалит за сотню, то проще будет воспользоваться специальной формулой для обработки.
Итак, нам понадобится значение первого числа в ряду (a1) и последнего (an), а также информация об общем количестве чисел в ряду. Рекуррентная формула, показывающая, как искать сумму, будет выглядеть в таком случае следующим образом:
Обратите внимание: под значением n подразумевается именно количество членов ряда, для которых производится нахождение суммы.
Произведение членов арифметической прогрессии можно находить по похожей формуле:
где, Pn – произведение, b1 и bn – соответственно первое и последнее числа, а n – количество членов.
Отдельно следует коснуться такого понятия, как характеристическое свойство прогрессии. Оно сводится к выполнению определенного условия для каждого элемента:
Примеры задач с решением
Рассмотрим как решать задачи на заданную тему.
Пример 1
Требуется вычислить 574 член в ряду арифметической прогрессии, первые три члена которой «8, 15, 22…».
Вариант рассуждений по примеру 1. Для нахождения любого конкретного элемента ряда нам необходима информация о значении первого члена (a1) и о разности (d). Чтобы вычислить разность, вычитаем из второго члена ряда первый (15 – 
Подставляя полученные значения, получим выражение вида a574 = 8 + (574-1) * 7.
После вычисления получаем ответ: a574 = 4019.
Пример 2
Требуется вычислить 544 член ряда, являющийся арифметической прогрессией, при условии, что 154-ый член равен 17, а разность (d) равна 8.
Вариант рассуждений по примеру 2. Пользоваться в данной ситуации мы будем формулой из предыдущего примера:
Подставляя известные значения, получаем выражение – а544 = 17 + (544 1) * 8.
Вычисляя, получаем ответ а544 = 4361.
Пример 3
Для подготовки к экзамену по биологии студенту Смирнову необходимо выучить 730 вопросов (включая загадки). Известно, что он весьма обеспокоен и по мере приближения даты экзамена учит ежедневно на 27 вопросов больше, чем в предыдущий день. Друг Смирнова выяснил, что тот в первый день выучил всего 17 вопросов.
Требуется выяснить, сколько времени у студента ушло на подготовку.
Вариант рассуждений по примеру 3. Очевидно, что случай с подготовкой студента к экзамену решается через формулы арифметической прогрессией (поскольку присутствует фиксированная разность d = 17). Производим подстановку известных данных:
После подстановки получаем выражение: 730 = 17 + (n 1) * 27.
После вычислений определяем ответ – 27 дней.
Арифметическая прогрессия является наиболее простой из всех числовых зависимостей. Использование описанных формул позволит намного ускорить вычисления в задачах, где это требуется.
Кроме этого, для упрощения можно использовать онлайн калькулятор. В школе данную тему изучают в программе за 9 класс, а основные задания касаются нахождения членов и сумм.