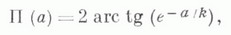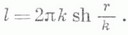Геометрия лобачевского это что

Лобачевского геометрия

Полезное

Смотреть что такое «Лобачевского геометрия» в других словарях:

ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ — построенная в 1826 Н. И. Лобачевским геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы (постулата) о параллельных. Евклидова аксиома гласит: в плоскости через точку, не… … Большой Энциклопедический словарь

Лобачевского геометрия — построенная в 1826 Н. И. Лобачевским геометрическая теория, основана на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы (постулата) о параллельных. Евклидова аксиома гласит: в плоскости через точку, не лежащую… … Энциклопедический словарь

Лобачевского геометрия — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия

ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ — геометрия, основанная на тех же основных посылках, что и евклидова геометрия, за исключением аксиомы о параллельных (см. Пятый постулат). В евклидовой геометрии согласно этой аксиоме на плоскости через точку Р, лежащую вне прямой А А, проходит… … Математическая энциклопедия

Лобачевского геометрия — геометрическая теория, основанная на евклидовых аксиомах, за исключением аксиомы о параллельных, которая заменяется на противоположную, аксиому Лобачевского: «Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие… … Начала современного естествознания

ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ — (неевклидова геометрия), геометрическая теория (1826), построенная великим русским математиком Н. И. Лобачевским. Ученый доказал, что геометрия Евклида есть только одна из нескольких равноправных геометрий, одинаково безупречных, одинаково… … Русская история

ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ — построенная в 1826 Н. И. Лобачевским геом. теория, осн. на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы (постулата) о параллельных. Евклидова аксиома гласит: в плоскости через точку, не лежащую на данной… … Естествознание. Энциклопедический словарь

Геометрия Лобачевского — (1) евклидова геометрия; (2) геометрия Римана; (3) геометрия Лобачевского Геометрия Лобачевского (гип … Википедия

геометрия — и; ж. [греч. gē Земля и metreō измеряю]. Раздел математики, изучающий пространственные формы и отношения. // Учебный предмет, излагающий этот раздел математики. Урок геометрии. Преподаватель геометрии. // Разг. Учебник по этому предмету. * * *… … Энциклопедический словарь

Источник

ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ

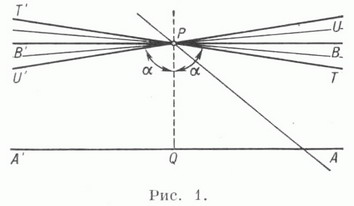
геометрия, основанная на тех же основных посылках, что и евклидова геометрия, за исключением аксиомы о параллельных (см. Пятый постулат). В евклидовой геометрии согласно этой аксиоме на плоскости через точку Р, лежащую вне прямой А’А, проходит только одна прямая В’В, не пересекающая А’А. Прямая В’В наз. параллелью к А ‘А. При этом достаточно потребовать, чтобы таких прямых проходило не более одной, так как существование непересекающей прямой может быть доказано путем последовательного проведения прямых В Л. г. аксиома параллельности требует, чтобы через точку Р(рис. 1) проходило более

одной прямой, не пересекающей А ‘А. Непересекающие прямые заполняют часть пучка с вершиной Р, лежащую внутри пары вертикальных углов TPU и U’PT’, расположенных симметрично относительно перпендикуляра PQ. Прямые, образующие стороны вертикальных углов, отделяют пересекающие прямые от непересекающих и сами являются тоже непересекающими. Эти граничные прямые наз. параллелями в точке Рк прямой А’А соответственно в двух ее направлениях: Т’Т параллельно А’А в направлении A’A, a UU’ параллельно А’А в направлении АА’. Остальные непересекающие прямые наз. расходящимися прямыми с А’А (подробнее см. ниже).

Угол к-рый параллель к точке Робразует с перпендикуляром наз. углом параллельности отрезка PQ=a и обозначается через При а=0 угол при увеличении а угол a уменьшается так, что для каждого заданного a, существует определенное значение а. Эта зависимость наз. Лобачевского функцией:

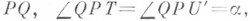
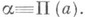
Евклидова геометрия может быть получена как предельный случай Л. г., когда обе параллели, проходящие через Р, сливаются в одну, т. е. когда множество всех прямых, проходящих через точку Ри непересекающих данную прямую А’А, сводится к единственной прямой. Тогда угол при любом а. Это условие эквивалентно требованию В малых областях пространства, т. е. когда линейные размеры фигур по отношению к kбесконечно малы, все соотношения Л. г. аппроксимируются получающимися в пределе соотношениями евклидовой геометрии.

Две различные прямые по плоскости образуют пару одного из трех типов.

Пересекающиеся прямые. Расстояние от точек одной прямой до другой прямой неограниченно увеличивается при удалении точки от пересечения прямых. Если прямые не перпендикулярны, то каждая проектируется ортогонально на другую в открытый отрезок конечной величины.

Расходящиеся прямые. Они имеют один общий перпендикуляр, отрезок к-рого дает минимальное расстояние. По обе стороны от перпендикуляра прямые неограниченно расходятся. Каждая прямая проектируется на другую в открытый отрезок конечной величины.

Вращение аналогов окружностей вокруг прямой порождающего пучка приводит к аналогам Сферы: собственно сфере, поверхности равных расстояний и о р и с ф е р е, или предельной поверхности.

Связь между длинами дуг и хорд предельных линий и евклидовы тригонометрии, соотношения на предельной поверхности позволяют вывести тригонометрич. соотношения на плоскости, то есть тригонометрич. формулы для прямолинейных треугольников. Напр., формулу для площади а треугольника:

для длины окружности:

Тригонометрич. формулы Л. г. могут быть получены из формул сферич. геометрии заменой радиуса Rна мнимое число ki.

Доказательство непротиворечивости Л. г. проводится с помощью построения интерпретации (модели). Первой такой интерпретацией явилась Белътрами интерпретация, где установлено, что в евклидовом пространстве внутренняя геометрия поверхности постоянной отрицательной гауссовой кривизны локально совпадает с Л. г. (роль прямых играют геодезические линии поверхности). Поверхность такого типа называется псевдосферой.

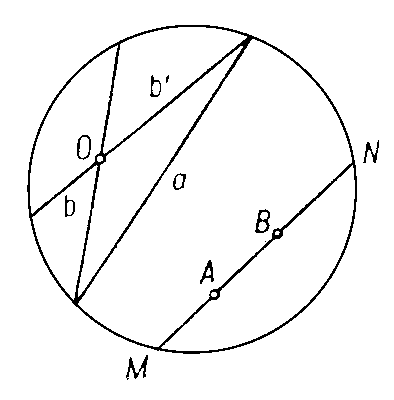
[стороны угла н проходящие через вершину касательные (мнимые) к абсолюту]. Параллели через точку Рк прямой MN реализуются прямыми РТ и пересекающими прямую MN в точках на абсолюте. Точки абсолюта моделируют «бесконечно удаленные точки», не являющиеся точками плоскости Лобачевского.

Введение тех или иных координат позволяет получать различные аналитич. модели плоскости Лобачевского. А. Пуанкаре была предложена (1887) модель Л. г. как геометрии плоских диаметральных сечений на одной из полостей двуполостного гиперболоида, к-рую можно трактовать и как геометрию сферы чисто мнимого радиуса в псевдоевклидовом пространстве. Указанные модели обобщаются на случай n-мерного пространства.

Как риманова геометрия, Л. г. есть геометрия риманова пространства постоянной отрицательной кривизны.

Источником создания Л. г. послужила проблема параллелей, т. е. попытки доказательства пятого постулата Евклида о параллельных. Н. И. Лобачевский (1826, опубл. 1829-30) показал, что допущение постулата, отличного от постулата Евклида, позволяет построить более общую, чем евклидова, Л. г. Независимо от Н. И. Лобачевского к этому открытию пришел Я. Больяй (J. Bolyai, 1832). Не получив открытой поддержки у К. Гаусса (С. Gauss), Я. Больяй не продолжил своих исследований.

К. Гаусс разрабатывал начала новой геометрии в значительно более ранние годы, но он не публиковал этих исследований и никогда не высказывался открыто об этих идеях. Однако в частной переписке он высоко оценил труды Я. Больяй и Н. И. Лобачевского, но открыто в печати все-таки не высказался.

Приложения геометрии Лобачевского. Н. И. Лобачевский уже в первой работе по Л. г. показал, опираясь на впервые измеренные астрономами в те годы годичные параллаксы звезд, что если в физич. пространстве реализуется его геометрия, то в пределах Солнечной системы отклонения от евклидовой геометрии будут на несколько порядков меньше возможных ошибок измерений. Таким образом, первым приложением Л. г. явилось обоснование практич. точности евклидовой геометрии.

Н. И. Лобачевский применял свою геометрию в математич. анализе. Переходя от одной системы координат к другой в своем пространстве, он нашел значения около 200 различных определенных интегралов. Др. математич. приложения были найдены А. Пуанкаре (1882), к-рый успешно применял Л. г. при разработке теории автоморфных функций.

Значение Л. г. для космологии было выявлено А. А. Фридманом. В 1922 он нашел решение уравнения Эйнштейна, из к-рого следовало, что Вселенная расширяется с течением времени. Это заключение впоследствии было подтверждено наблюдениями Э. Хаббла (Е. Hubble, 1’929), обнаружившего разбегание удаленных туманностей. Метрика, найденная А. А. Фридманом, дает при фиксированном времени пространство Лобачевского. Пространство скоростей специальной теории относительности является пространством Лобачевского.

Л. г. с успехом используется при изучении столкновений элементарных частиц и при разработке др. вопросов ядерных исследований.

Зрительное (перцептивное) восприятие близких областей пространства человеком порождает эффект обратной перспективы, объясняемый тем, что геометрия этих областей перцептивного пространства близка к Л. г. с радиусом кривизны около 15 м.

Создание Л. г. явилось важным этапом в развитии учения о возможных свойствах пространства. Особенное значение это имело для оснований математики, т. к. принципы современного аксиоматич. метода вырабатывались в значительной степени благодаря появлению Л. г.

Лит.:[1] Лобачевский Н. И., Полн. собр. соч., т. 1-5, М.- Л., 1946-51; [2] Больаи Я., Appendix, пер. с латин., М.- Л., 1950; [3] Александров А. Д., Абстрактные пространства, в кн.: Математика, се содержание, методы и значение, т. 3, М., 1956; [4] Егоров И. П., Введение в неевклидовы геометрии, Пенза, 1972; [5] Ефимов Н. В., Высшая геометрия, 6 изд., М., 1978; [6] Каган В. Ф., Основания геометрии, ч. 1, М.- Л., 1949; [7] Лаптев Б. Л., Николай Иванович Лобачевский, Казань, 1976; [8] Норден А. П., Элементарное введение в геометрию Лобачевского, М., 1953; [9] Нут Ю. Ю., Геометрия Лобачевского в аналитическом изложении, М., 1961: [10] Раушенбах Б. В., Пространственные построения в древнерусской живописи, М., 1975; [11] Розенфельд Б. А., Неевклидовы пространства, М., 1969; [12] Широков П. А., Краткий очерк основ геометрии Лобачевского, Казань, 1964. Б. Л. Лаптев.

Источник

Геометрия Лобачевского

Дата публикации: 20.12.2016 2016-12-20

Статья просмотрена: 2079 раз

Библиографическое описание:

Бокова, К. Д. Геометрия Лобачевского / К. Д. Бокова, И. Г. Майоров, Д. В. Козлова, Н. Ю. Потапова. — Текст : непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 13-15. — URL: https://moluch.ru/young/archive/9/626/ (дата обращения: 16.12.2021).

1. Постановка проблемы

Все мы в школе проходим курс геометрии — науки, в которой кто-то не видит смысла, а иные находят свое призвание. При этом мы изучаем Евклидову геометрию, зародившуюся более двух тысяч лет назад, но и сейчас остающуюся актуальной. Но почти все слышали и о других, так называемых неевклидовых геометриях, в частности — о геометрии Лобачевского. И самое странное, что знакомство с этой наукой заканчивалось на утверждении, что она допускает возможность пересечения параллельных прямых. Этот факт удивляет, даже поражает, но, как и все непонятное, воспринимается на веру.

А ведь на самом деле геометрия Лобачевского не так уж сильно отличается от привычной нам геометрии и тот факт, что параллельные прямые в ней пересекаются — это досужий миф, родившийся при странных обстоятельствах. Но, для того чтобы это понять, необходимо хотя бы вкратце разобрать историю появления геометрии как науки.

Пятый постулат геометрии Лобачевского утверждает, что если на плоскости лежат прямая иточка, то через эту точку можно провести хотя бы две прямые, не пересекающиеся спервой прямой.

Рис.1 Иллюстрация пятого постулата

А в геометрии Евклида через точку А можно провести только одну-единственную прямую. Таким образом, неевклидова геометрия допускает, что на одной плоскости может находиться сразу несколько прямых линий, не пересекающихся друг с другом.

А утверждение о возможности пересечения параллельных прямых в геометрии Лобачевского возникло из-за простого незнания аксиом этой геометрии. Ведь при ближайшем рассмотрении оказывается, что в неевклидовой геометрии не только не говорится о пересечении параллельных прямых, но и не говорится о параллельных прямых вообще — разговор здесь идет именно о непересекающихсяпрямых, находящихся на одной плоскости.

2. Лобачевский Николай Иванович

Рис.2. Лобачевский Н. И.

Лобачевский и не подозревал о своём могучем таланте математика. Будучи студентом первого курса Казанского университета, он изучал медицину. Деятельность Лобачевского неразрывно связана с историей Казанского университета, который был открыт в 1805 году. В 1827 году Николай Иванович становится ректором Казанского университета, находится он в этой должности непрерывно в течение 19 лет.

Деятельность Лобачевского вызывает изумление. Наряду с большой административной и педагогической работой он, не покладая рук, занимался и наукой. Ему было всего 34 года, когда он решил «многовековую» проблему V постулата из «Начал» Евклида и построил свою, неевклидову геометрию.

Имя Лобачевского известно всему миру. Он вошёл в историю математики как революционер в науке и «Коперник геометрии». Он решил проблему, над которой человечество бесплодно билось более двух тысяч лет. Анализируя попытки доказать V постулат, Лобачевский сделал чрезвычайно смелый вывод о его недоказуемости.

Геометрия со времен Евклида стала аксиоматической теорией, в которой большинство утверждений доказывалось на основе нескольких аксиом (постулатов). Считалось, что эти аксиомы «очевидны», т. е. отражают свойства реального (физического) пространства.

Одна из этих аксиом вызывала у ученых подозрение: а нельзя ли ее вывести из остальных постулатов? Современная формулировка этой аксиомы такова: «Через точку, не лежащую на заданной прямой, можно провести не более одной прямой, параллельной ей». То, что одну прямую можно провести, является не аксиомой, а теоремой.

При этом «параллельной» называется прямая, не пересекающая данную. Итак, суть аксиомы в том, что такая прямая — одна.

То есть, распространенное утверждение «Лобачевский доказал, что параллельные прямые могут и пересекаться» — является в корне неверным. Ведь это бы противоречило их определению.

Евклидова геометрия

Параллельнымипрямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. (В некоторых определениях совпадающие прямые не считаются параллельными). В свою очередь, существование непересекающихся в плоскости прямых является фактом абсолютной геометрии, т. е. фактом, который может быть доказан и без использования аксиомы Евклида, и без использования аксиомы Лобачевского. А именно, верно следующее утверждение: Если две прямые (в плоскости) перпендикулярны третьей, то они не пересекаются. В планиметрии Евклида любые непересекающиеся прямые — параллельны, в планиметрии Лобачевского это не так.

Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство лишь евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две).

Аксиомы Евклида

1. Аксиома принадлежности. Через любые две точки на плоскости можно провести прямую и притом только одну.

2. Аксиома порядка. Среди любых трёх точек, лежащих на прямой, есть не более одной точки, лежащей между двух других.

3. Аксиома конгруэнтности (равенства) отрезков и углов. Если два отрезка (угла) конгруэнтны третьему, то они конгруэнтны между собой.

4. Аксиома непрерывности (аксиома Архимеда). Для любых двух отрезков AB и CD существует конечный набор точек A₁, A₂,…, A_n, лежащих на прямой AB, таких, что отрезки AA₁, A₁A₂,…, A_{n — 1}A_n конгруэнтны (сравнимы) отрезку CD, a точка B лежит между A и A_n.

5. Аксиома параллельных прямых. Через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.

Среди пяти аксиом Евклида пятая резко выделяется своей неочевидностью. Она больше похожа на теорему: через точку, не лежащую на данной прямой, проходит ровно одна прямая, параллельная данной.

Многие учёные пытались вывести пятую аксиому из первых четырех. Среди них древнегреческие математики Птолемей и Прокл, иранский математик Омар Хайям, немецкие математики Клавиус и Ламберт, английский математик Валлис и многие другие.

Возникла мысль, что можно построить геометрию, где через точку, не лежащую на прямой, проходят по крайней мере две прямые, ей параллельные. 23 февраля 1826 года на заседании математического факультета Казанского университета российский математик Николай Иванович Лобачевский заявил, что пятый постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную и свободную от противоречий, как и евклидова.

Одновременно к аналогичным выводам пришёл Янош Бойяи, а Карл Фридрих Гаусс пришёл к таким выводам ещё раньше.

Однако труды Бойяи не привлекли внимания, и он вскоре оставил эту тему, а Гаусс вообще воздерживался от публикаций. В итоге Н.Лобачевский выступил как первый наиболее яркий и последовательный пропагандист новой геометрии.

Лобачевский, как и многие до него, решил доказать, что это утверждение можно вывести из других аксиом. Для этого он выбрал метод «от противного», т. е. предположил, что прямых, не пересекающих данную, больше одной и попытался вывести из этого противоречие с другими фактами. Но чем дальше он развивал теорию, тем больше убеждался, что никакого противоречия не предвидится. (Т. е. получалось, что теория с «неправильным» постулатом тоже имеет право на существование.)

Конечно, в первое время его выкладки не признавали. Именно поэтому великий Гаусс (который пришел к тем же выводам) не рискнул опубликовать свои результаты. Но со временем пришлось признать, что, основываясь на логике, теория Лобачевского ничем не хуже евклидовой.

Один из простых, но хитрых способов убедиться в этом — придумать такие «прямые», которые ведут себя как «прямые» Лобачевского. И математики нашли такой пример, и не один. Пожалуй, самой простой является модель Пуанкаре. Её возможно построить самим, при чем довольно легким способом.

Рис. 3. Модель Пуанкаре

Для того всего лишь потребуется: начертить на листке бумаги прямую. Взять циркуль и, ставя его иглу на эту прямую, нарисовать полуокружности, находящиеся с одной стороны от прямой. Затем стереть прямую (и с ней — концевые точки полуокружностей). Эти полуокружности «без концов» и будут вести себя, как прямые в геометрии Лобачевского.

Выделим одну полуокружность и точку вне нее. Есть достаточно много полуокружностей, которые не пересекаются с исходной и все проходят через данную точку. Среди них выделяются две: они касаются нашей исходной «прямой» в концевых точках (которые мы, как Вы помните, стерли), т. е. реального пересечения не происходит. Эти две окружности задают «границы», между которыми находятся все прямые, не пересекающие данную. Их — бесконечное множество.

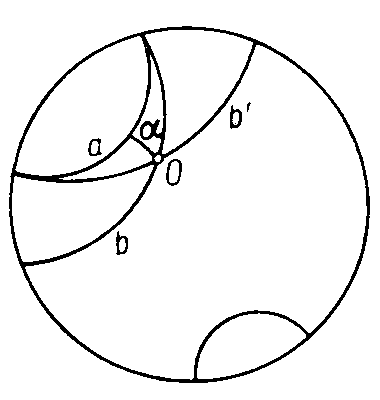
За плоскость Лобачевского принимается внутренность круга, прямыми считаются дуги окружностей, перпендикулярных окружности данного круга, и его диаметры, движениями — преобразования, получаемые комбинациями инверсий (Инверсия представляет собой более сложное преобразование геометрических фигур, при котором прямые уже могут переходить в окружности) относительно окружностей, дуги которых служат прямыми. В геометрии Лобачевского прямые на плоскости либо пересекаются, либо параллельны, либо являются расходящимися.

Рис. 4. Прямые в геометрии Лобачевского

В геометрии Лобачевского сохраняются все теоремы, которые можно доказать без использования аксиомы параллельности. В геометрии Лобачевского нет подобных треугольников. В геометрии Лобачевского имеет место четвертый признак равенства треугольников: если углы одного треугольника соответственно равны углам другого треугольника, то эти треугольники равны.

Все! Перечеркнуты «Начала». Довольно мысль на них скучала.

Хоть прав почти во всем Евклид, но быть не вечно постоянству.

И плоскость свернута в пространство, и мир иной имеет вид.

Модели геометрии Лобачевского дали доказательство её непротиворечивости, точнее показали, что геометрия Лобачевского столь же непротиворечива, как геометрия Евклида.

Петербургский ученый А. А. Фридман в 1922 обнаружил, что Вселенная расширяется и является пространством Лобачевского. Отклонения геометрии Лобачевского от евклидовой геометрии растут с увеличением размеров. Впрочем, в наше время ни физики, ни, тем более, математики, не пытаются воспринимать геометрию Лобачевского как модель «реального», физического пространства, ибо в пределах солнечной системы, и даже нашей галактики, эти размеры так малы, что погрешность измерений не позволяет их обнаружить. Вот почему, живя в пространстве Лобачевского, мы пользуемся геометрией Евклида!

За год до смерти, будучи совершенно слепым, Лобачевский диктует своим ученикам новое сочинение, названное им «Пангеометрией», где показывает, что евклидова геометрия есть частный случай неевклидовой геометрии. Эту последнюю свою работу он с любовью посвящает Казанскому университету, где прошла вся его творческая жизнь.

Заключение

Таким образом, мы представили вам одну из самых на первый взгляд невероятных и противоречивых теорем. Теорема Лобачевского в начале кажется сложной и непонятной, но вызывает огромный интерес (по крайней мере, таковой она вызвала у нас). А все, что вызывает интерес должно быть изучено, что мы и сделали. При подробном её рассмотрении теорема оказывается вполне логичной, и потому простой для восприятия.

Гений Лобачевского в том, что он смог выйти за поставленные многовековыми устоями границы, смог доказать то, что практически все наши знания весьма и весьма относительны. И все может быть устроено вовсе не так, как мы привыкли это воспринимать. Его смелая идея помогает расширить кругозор, помогает по-иному взглянуть на привычный нам мир. И потому эта теорема достойна, во-первых, существования, и, во-вторых, признания её в нашем обществе.

Источник