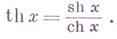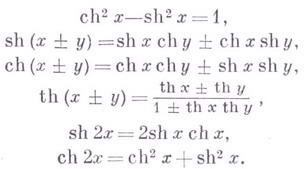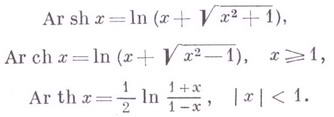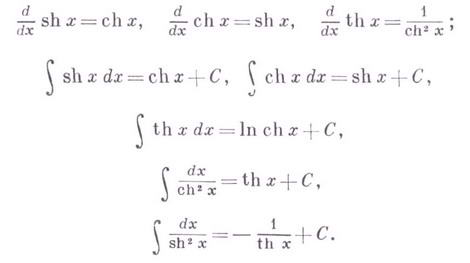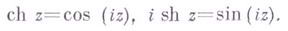Гиперболический косинус чему равен
Гиперболические функции
Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.
Содержание
Определение
Определение гиперболических функций через гиперболу
Один из способов определения тригонометрических функций через единичную окружность
Гиперболические функции задаются следующими формулами:
Существует сленговые названия: «шинус», «шимус»(?). Однако их использование не научно.
Существует сленговые названия: «чосинус», «кошинус». Однако их использование не научно.
Существует сленговые названия: «щангенс», «тахинус». Однако их использование не научно.
Иногда также определяются
Существует сленговые названия: «кочангенс», «кохинус». Однако их использование не научно.
Геометрическое определение
Ввиду соотношения 







Свойства
Связь с тригонометрическими функциями
Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.

Важные тождества
Разложение в степенные ряды
Здесь 
Графики
Аналитические свойства
Гиперболический синус и гиперболический косинус аналитичны во всей комплексной плоскости, за исключением существенно особой точки на бесконечности. Гиперболический тангенс аналитичен везде, кроме полюсов в точках 


Обратные гиперболические функции
Читаются ареа… (-синус и т. д.) — от лат. «area» — «площадь».







Эти функции имеют следующее разложение в ряд:

История
Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы.
Применение
Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций.
Ссылки
cs:Hyperbolická funkce he:פונקציות היפרבוליות hu:Hiperbolikus függvények is:Breiðbogafall nl:Hyperbolische functie pl:Funkcje hiperboliczne sr:Хиперболичне функције sv:Hyperbolisk funktion
Гиперболические функции
Содержание:
Гиперболические функции
Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.
Основные понятия:
Рассмотрим единичную окружность с центром в начале координат, уравнение которого имеет вид х 2 + у 2 = 1.
Согласно определению, синусом угла 
Докажем, что площадь сектора АОВ равна числовому значению угла AOD, взятом в радианах.
Действительно, если R=1, а угол сектора АОВ- 
Следовательно, в тригонометрических функциях за аргумент можно принимать не только угол, а и площадь соответствующего сектора.
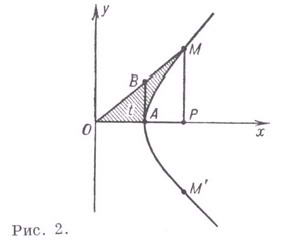
Рассмотрим теперь равнобокую гиперболу с асимптотами 
Повторим предыдущие рассуждения:
— выберем на гиперболе т. А(х, у);
— проведём радиусы ОА и ОВ (
Образовавшуюся фигуру OANB называют гиперболическим сектором (сектором 
Возьмём за аргумент площадь гиперболического сектора 
Найдём площадь гиперболического сектора, как разность площади треугольника АОВ и криволинейной трапеции ANB.
Потому, что фигура симметрична, имеем
либо, решив систему
Аналогично как в тригонометрии вводят понятия тангенса и котангенса
Свойства гиперболических функций
Чётность и нечётность проверим подставив (-х) в соответствующие формулы
Следовательно, как и в тригонометрических функциях, имеем 

Остальные свойства легко установить построив графики гиперболических функций.
Для построения воспользуемся записью
то есть графики функций
Полученные графическим сложением ординат графики функций 
Графики 
Видим, что в отличии от тригонометрических, гиперболические функции непериодические. Основные свойства каждой из гиперболических функций указаны в опорном конспекте (п. 10.5).
Дифференцирование и интегрирование гиперболических функций
Гиперболические функции можно дифференцировать и интегрировать. Выведем формулы производных и интегралов.
Переход от гиперболических функций к тригонометрическим и наоборот
Используя гиперболические функции можно вывести формулы Эйлера. Действительно, вспомним разложение в ряд Маклорена функций
Положим в разложении функции у=е х за аргумент х=zj. Получим:
Учитывая, что 

Именно эти формулы позволяют установить зависимость между тригонометрическими и гиперболическими функциями.
Принимаем без доказательств, что все тригонометрические формулы действительны и для воображаемого аргумента. Это предположение позволит установить зависимость между гиперболическими функциями.
Аналогично можно получить формулы для
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Гиперболический синус производная, график функции, формула через экспоненту, чему равен, разложение, свойства, связь с гиперболическим косинусом
В электротехнике, механике, теории чисел, геометрии Лобачевского, химии, экономике для удобства расчётов наравне с тригонометрическими функциями используют гиперболический синус.
Название термина впервые введено Риккати в 1757 году при исследовании свойств различных кривых второго порядка. Его работа была продолжена Ламбертом, а затем и другими учёными-математиками.
Определение, формула и график гиперболического синуса
Математика позволяет дать два подхода к определению, благодаря различным направлениям в изучении объекта.
Первый, отталкиваясь от задающей формулы, позволяет установить связи между объектами, второй, полученный благодаря исследованиям в аналитической геометрии, демонстрирует наглядное (образное) понимание происходящего.
Гиперболический синус (традиционно обозначается shx, онлайн-калькулятор, вычислительные программы используют вместо него sinh(x)) – элементарная функция, представляемая как
С другой стороны, ординаты точек равнобокой гиперболы:
заданные через параметр, принимают за определение гиперболического синуса как функции удвоенной площади сектора, образованного радиус-вектором OM (M – точка кривой) и отрезком OA (A – вершина):
График y = shx имеет вид:
Чтобы его построить, достаточно знать ряд значений. Существующая таблица, онлайн-калькуляторы и специальные программы значительно облегчают вычисления.
Связь с тригонометрическими функциями
Рассматривая все компоненты на множестве комплексных чисел, используя тождество Эйлера, позволяющее связать тригонометрические функции и экспоненту, можно получить соотношения y = shx и некоторых других элементарных отображений переменных:
Во всех случаях x – действительное число.
Свойства гиперболического синуса
shx — гиперболический синус обладает следующими свойствами:
функция аналитична во всей комплексной плоскости, кроме существенно особой точки на бесконечности;
монотонно возрастает на всей области определения. При x → +∞ увеличение ординат точек происходит достаточно быстро. Поэтому часто происходит замена на e x /2;
обладает свойствами, аналогичными формулам тригонометрии, основное из которых является следствием второго определения:
где chx – гиперболический косинус.
Другие важные тождества:
Производная вычисляется согласно общим правилам:
Вычисление интеграла есть обратный процесс к нахождению производной, значит:
Примеры решения задач
Помимо непосредственной работы с этой функцией, важную роль играют тождества, позволяющие значительно упростить вычисления.
При интегрировании иррациональных функций, удобно делать замену, учитывая, что единицу можно представить как разность гиперболических синуса и косинуса:
Определить, какому семейству первообразных равен интеграл
Решение. Делается замена переменной:
После подстановки получается интеграл:
Делая возврат к исходной переменной, получается итоговое решение.
Основные гиперболические функции:
из которых получены:
соответствующие производным тригонометрическим функциям.
СОДЕРЖАНИЕ
Определения
Существуют различные эквивалентные способы определения гиперболических функций.
Экспоненциальные определения
Определения дифференциальных уравнений
Сложные тригонометрические определения
Гиперболические функции также могут быть выведены из тригонометрических функций со сложными аргументами:
Приведенные выше определения связаны с экспоненциальными определениями через формулу Эйлера (см. § Гиперболические функции для комплексных чисел ниже).
Характерные свойства
Гиперболический косинус
Можно показать, что площадь под кривой гиперболического косинуса (на конечном интервале) всегда равна длине дуги, соответствующей этому интервалу:
площадь знак равно ∫ а б шиш Икс d Икс знак равно ∫ а б 1 + ( d d Икс шиш Икс ) 2 d Икс знак равно длина дуги. <\ displaystyle <\ text> = \ int _ ^ \ cosh x \, dx = \ int _ ^ <\ sqrt <1+ \ left (<\ frac
Гиперболический тангенс
Полезные отношения
Нечетные и четные функции:
Гиперболический синус и косинус удовлетворяют:
У одного также есть
для других функций.
Суммы аргументов
Формулы вычитания
Формулы половинного аргумента
Квадратные формулы
Неравенства
Это можно доказать, почленно сравнивая ряды Тейлора этих двух функций.
Обратные функции как логарифмы
Производные
Вторые производные
Стандартные интегралы
Следующие интегралы можно доказать с помощью гиперболической замены :
Выражения ряда Тейлора
Сравнение с круговыми функциями
Катеты двух прямоугольных треугольников с гипотенузой на луче, определяющем углы, имеют длину √ 2 раза больше круговой и гиперболической функций.
Функция Гудермана дает прямую связь между круговыми функциями и гиперболическими функциями, не содержащими комплексных чисел.
Связь с экспоненциальной функцией
Разложение экспоненты на четную и нечетную части дает тождества
Гиперболические функции для комплексных чисел
Связь с обычными тригонометрическими функциями задается формулой Эйлера для комплексных чисел:
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
функции, определяемые формулами:


Иногда рассматривается также гиперболический тангенс;
Другие обозначения: sinh x,Sh x,cosh x, Ch x,tgh x,tanh x,Th x. Графики см. на рис. 1.
Производные и основные интегралы от Г. ф.:
Во всей плоскости комплексного переменного z Г. ф. 
Полезное
Смотреть что такое «ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ» в других словарях:
Гиперболические функции — функции, определяемые формулами: (гиперболический синус), (гиперболический косинус). Иногда рассматривается также гиперболический тангенс: (графики Г. ф. см. на рис. 1). Г. ф.… … Большая советская энциклопедия
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — функции, определяемые формулами: (гиперболический синус), (гиперболический косинус), (гиперболический тангенс) … Большой Энциклопедический словарь
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — функции, определяемые формулами: shx = (ex e x)/2(гинерболич. синус), chх (еx + е к)/2 (гиперболич. косинус), thх = shx/chx (гиперболич. тангенс). Графики Г. ф. см. на рис … Естествознание. Энциклопедический словарь
Гиперболические функции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Содержание 1 Определение 1.1 Геометрическое определение … Википедия
гиперболические функции — функции, определяемые формулами: shx = (ex – e x)/2 (гиперболический синус), chx = (ex + e x)/2 (гиперболический косинус), thx = shx/chx (гиперболический тангенс). Графики гиперболических функций см. на рис. * * * ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ… … Энциклопедический словарь
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — Функции. определяемые ф лами: (гиперболич. синус), (гиперболич. косинус), (вставить рисунки. ) Графики гиперболических функций … Большой энциклопедический политехнический словарь
Гиперболические функции — По аналогии с тригонометрическими функциями Sinx, cosx, определяемыми, как известно, при помощи Эйлеровых формул sinx = (exi e xi)/2i, cosx = (exi + e xi)/2 (где е есть основание нэперовых логарифмов, a i = √[ 1]); иногда вводятся в рассмотрение… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Обратные гиперболические функции — функции, обратные по отношению к гиперболическим функциям (См. Гиперболические функции) sh х, ch х, th х; они выражаются формулами (читается: ареа синус гиперболический, ареа косинус гиперболический, ареа тангенс… … Большая советская энциклопедия
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — функции, обратные к гиперболич. функциям; выражаются формулами … Естествознание. Энциклопедический словарь
Обратные гиперболические функции — Обратные гиперболические функции определяются как обратные функции к гиперболическим функциям. Эти функции определяют площадь сектора единичной гиперболы x2 − y2 = 1 аналогично тому, как обратные тригонометрические функции определяют длину… … Википедия