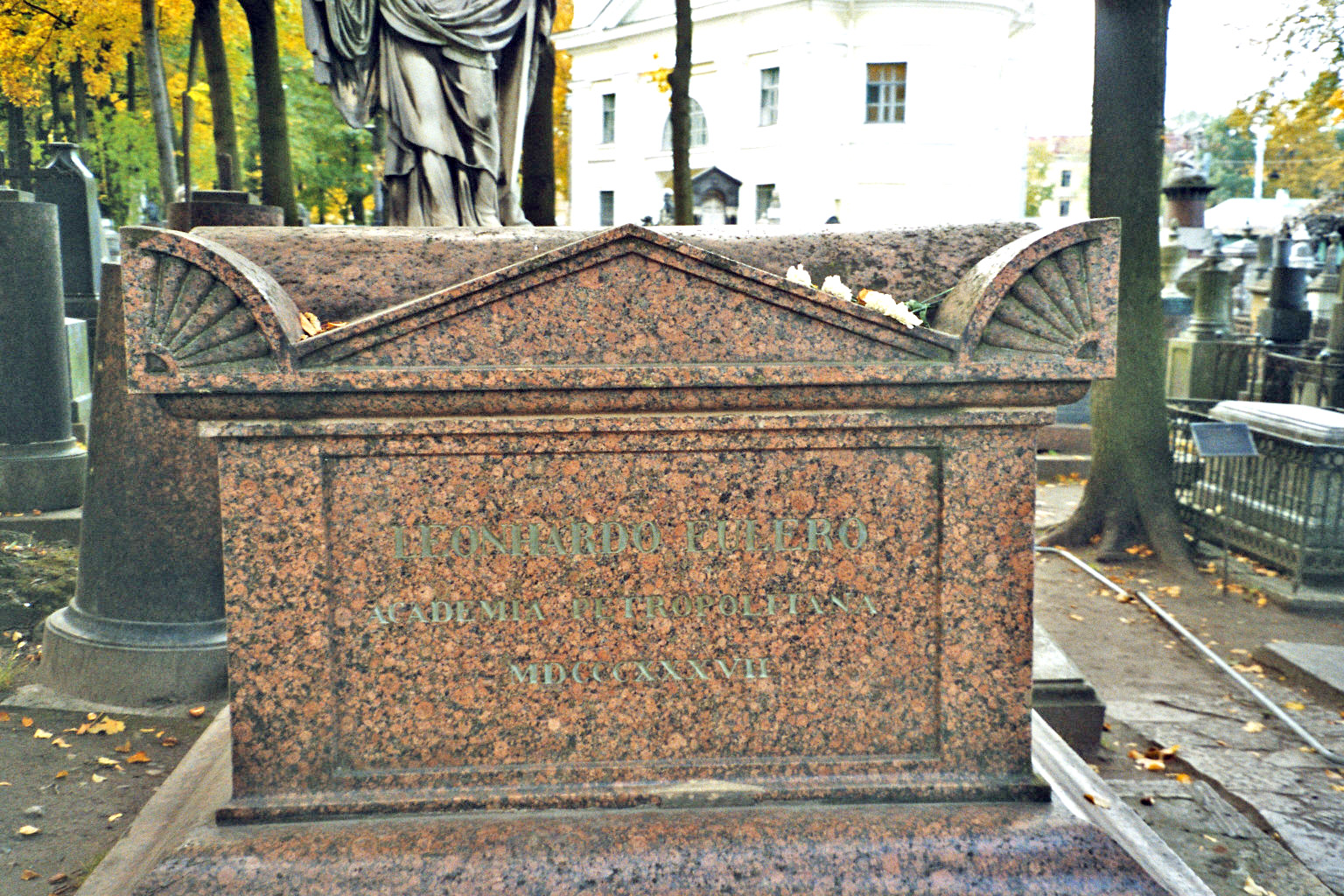кто такой эйлер и чем он знаменит
Леонард Эйлер
Леонард Эйлер (1707-1783) – швейцарский, немецкий и российский математик и механик, внесший огромный вклад в развитие этих наук (а также физики, астрономии и ряда прикладных наук). За годы своей жизни издал свыше 850 работ, касающихся самых разных областей.
Эйлер глубоко исследовал ботанику, медицину, химию, воздухоплавание, теорию музыки, множество европейских и древних языков. Был членом многих академий наук, являясь первым российским членом Американской академии искусств и наук.
В биографии Леонарда Эйлера есть множество интересных фактов, о которых мы расскажем в данной статье.
Итак, перед вами краткая биография Эйлера.
Биография Леонарда Эйлера
Леонард Эйлер появился на свет 15 апреля 1707 г. в швейцарском городе Базеле. Он рос и воспитывался в семье пастора Пауля Эйлера и его супруги Маргареты Брукер.
Стоит заметить, что отец будущего ученого увлекался математикой. На протяжении первых 2-х лет учебы в университете он посещал курсы известного математика Якоба Бернулли.
Детство и юность
Первые годы детства Леонарда прошли в селении Рихен, куда семейство Эйлеров переехало вскоре после рождения сына.
Начальное образование мальчик получил под руководством своего отца. Любопытно, что у него достаточно рано проявились математические способности.
Когда Леонарду было около 8 лет родители отправили его учиться в гимназию, которая находилась в Базеле. В тот момент биографии он проживал вместе с бабушкой по материнской линии.
В 13-летнем возрасте талантливому ученику разрешили посещать лекции в Базельском университете. Леонард настолько хорошо и быстро учился, что на него вскоре обратил внимание профессор Иоганн Бернулли, который был братом Якоба Бернулли.
Профессор предоставил юноше множество математических трудов и даже разрешил ему приходить к нему домой по субботам, для разъяснения труднопонимаемого материала.
Через несколько месяцев подросток успешно сдал экзамены в Базельский университет на факультет искусств. После 3-х лет обучения в вузе он удостоился ученой степени магистра, выступив с лекцией на латыни, в ходе которой сравнил систему Декарта с натуральной философией Ньютона.
В скором времени, желая угодить отцу, Леонард поступил на богословский факультет, продолжая активно заниматься математикой. Интересен факт, что позже Эйлер-старший разрешил сыну связать свою жизнь с наукой, поскольку осознавал его одаренность.
В то время биографии Леонард Эйлер опубликовал несколько научных работ, включая «Диссертацию по физике о звуке». Данная работа участвовала в конкурсе на освободившуюся должность профессора физики.
Несмотря на положительный отзыв, 19-летнего Леонарда сочли чересчур молодым, чтобы доверить ему профессорскую кафедру.
Вскоре Эйлер получил заманчивое приглашение от представителей Санкт-Петербургской академии наук, которая только находилась на пути своего становления и остро нуждалась в талантливых ученых.
Научная карьера в Санкт-Петербурге
В 1727 г. Леонард Эйлер приехал в Санкт-Петербург, где стал адъюнктом высшей математики. Российское правительство выделило ему квартиру и определило оклад в размере 300 рублей в год.
Математик сразу же начал учить русский язык, который смог освоить в сжатые сроки.
Позднее Эйлер подружился с Кристианом Гольдбахом – постоянным секретарем академии. Она вели активную переписку, которая сегодня признана важным источником по истории науки в 18 веке.
Данный период биографии Леонарда был необычайно плодотворен. Благодаря своим трудам он быстро приобрел мировую известность и признание со стороны научного сообщества.
Политическая нестабильность в России, прогрессировавшая после смерти императрицы Анны Ивановны, вынудила ученого выехать из Санкт-Петербурга.
В 1741 г., по приглашению прусского монарха Фридриха 2, Леонард Эйлер вместе с семьей отправился в Берлин. Немецкий король хотел основать академию наук, поэтому был заинтересован в услугах ученого.
Работа в Берлине
Когда в 1746 г. в Берлине открылась своя академия, Леонард занял должность руководителя математического отделения. Кроме этого ему доверили следить за обсерваторией, а также решать кадровые и финансовые вопросы.
Авторитет Эйлера, а с ним и материальное благополучие, с каждым годом росли. В результате, он стал настолько богат, что смог купить роскошное имение в Шарлоттенбурге.
Отношения Леонарда с Фридрихом 2 было сложно назвать простыми. Некоторые биографы математика полагают, что Эйлер держал обиду на прусского монарха за то, что тот не предложил ему должность президента Берлинской академии.
Эти и многие другие поступки короля, вынудили Эйлера покинуть Берлин в 1766 г. В то время он получил выгодное предложение от Екатерины 2, которая недавно взошла на престол.
Возвращение в Санкт-Петербург
В Петербурге Леонарда Эйлера встретили с большими почестями. Ему сразу же предоставили престижный пост и были готовы выполнять практически любые его просьбы.
Хотя карьера Эйлера продолжала стремительно развиваться, его здоровье оставляло желать лучшего. Катаракта левого глаза, беспокоившая его еще в Берлине, все больше прогрессировала.
В результате, в 1771 г. Леонарду была сделана операция, которая привела к абсцессу и фактически полностью лишила зрения.
Через несколько месяцев в Петербурге произошел серьезный пожар, который затронул и жилище Эйлера. Фактически ослепшего ученого чудом удалось спасти Питеру Гримму – мастеровому из Базеля.
По личному распоряжению Екатерины 2, для Леонарда был построен новый дом.
Несмотря на многие испытания, Леонард Эйлер никогда не переставал заниматься наукой. Когда по состоянию здоровья он уже не мог писать, математику помогал его сын Иоганн Альбрехт.
Личная жизнь
В 1734 г. Эйлер взял в жены Катарину Гзель, дочь швейцарского живописца. В этом браке у пары родилось 13 детей, 8 из которых умерли еще в детстве.
Стоит заметить, что его первый сын, Иоганн Альбрехт, в будущем также стал талантливым математиком. В 20-летнем возрасте он оказался в составе Берлинской академии наук.
Второй сын, Карл, занимался изучением медицины, а третий, Кристоф, связал свою жизнь с военной деятельностью. Одна из дочерей Леонарда и Катарины, Шарлота, стала женой голландского аристократа, а другая, Хелена, вышла замуж за русского офицера.
После приобретения усадьбы в Шарлоттенбурге, Леонард привез туда овдовевшую мать, сестру и обеспечил жильем всех своих детей.
В 1773 г. Эйлер лишился любимой супруги. Через 3 года он вступил в брак с Саломеей-Абигайль. Интересен факт, что его избранница была сводной сестрой его покойной жены.
Смерть
Великий Леонард Эйлер умер 18 сентября 1783 г. в возрасте 76 лет. Причиной его кончины стал инсульт.
В день смерти ученого на его 2-х грифельных досках были обнаружены формулы, описывающие полет на воздушном шаре. В скором времени в Париже на шаре совершат свой полет братья Монгольфье.
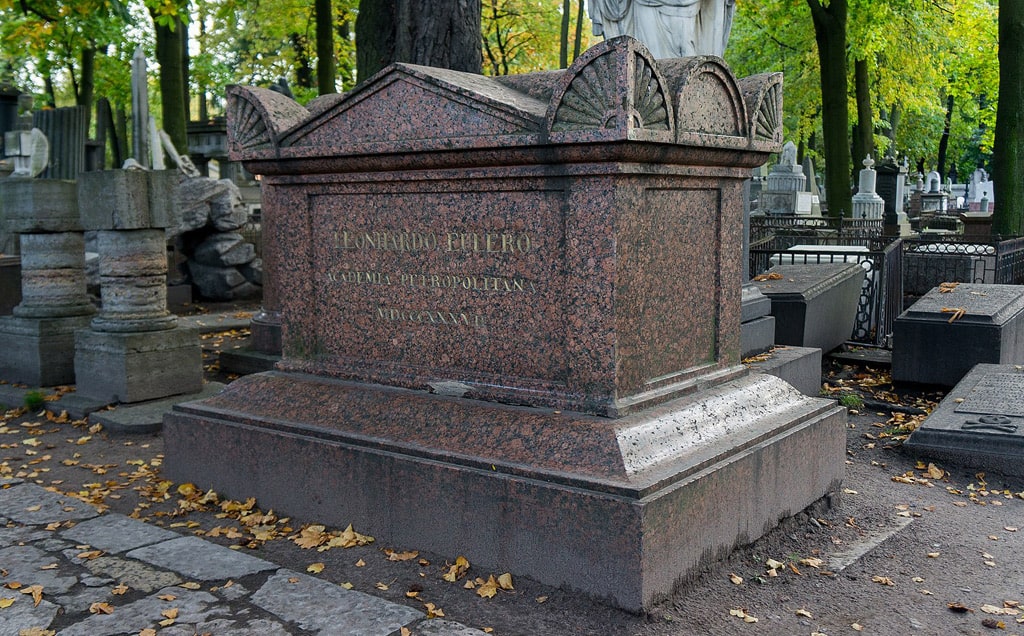
Вклад Эйлера в науку являлся настолько масштабным, что его статьи исследовались и печатались на протяжении еще 50 лет после кончины математика.
Научные открытия во время первого и второго пребывания в Санкт-Петербурге
В данный период биографии Леонард Эйлер глубоко изучал механику, теорию музыки и архитектуру. Он издал около 470 работ на самые разные темы.
Фундаментальный научный труд «Механика» затрагивал все области данной науки, включая небесную механику.
Ученый изучал природу звука, составив теорию удовольствия, вызываемого музыкой. При этом Эйлер присвоил интервалу тона, аккорду или их последовательности численные значения. Чем ниже была степень, тем выше оказывалось удовольствие.
Во второй части «Механики» Леонард уделил внимание судостроению и навигации.
Эйлер внес неоценимый вклад в развитие геометрии, картографии, статистики и теории вероятности. Отдельного внимания заслуживает 500-страничный труд «Алгебра». Интересен факт, что эту книгу он написал с помощью стенографиста.
Леонард глубоко исследовал теорию Луны, военно-морские науки, теорию чисел, натуральную философию и диоптрику.
Берлинские работы
Кроме 280 статей, Эйлер опубликовал множество научных трактатов. В период биографии 1744-1766 гг. он основал новый раздел математики – «вариационное исчисление».

Из-под его пера вышли трактаты по оптике, а также о траекториях планет и комет. Позже Леонард издал такие серьезные труды, как «Артиллерия», «Введение в анализ бесконечно малых», «Дифференциальное исчисление» и «Интегральное исчисление».
В течение всех лет, проведенных в Берлине, Эйлер исследовал оптику. В результате он стал автором трехтомной книги «Диоптрика». В ней он описывал разные способы усовершенствования оптических приборов, включая телескопы и микроскопы.
Система математических обозначений
Среди сотен наработок Эйлера наиболее заметной считается представление теории функций. Мало кому известен тот факт, что именно он первым ввел обозначение f(x) – функции «f» по аргументу «x».
Мужчина также вывел математические обозначения для тригонометрических функций в том виде, в каком они известны сегодня. Он стал автором символа «e», для образования натурального логарифма (известный как «число Эйлера»), а также греческую букву «Σ» для итоговой суммы и букву «i» для определения мнимой единицы.
Анализ
Леонард использовал показательные функции и логарифмы в аналитических доказательствах. Он изобрел метод, посредством которого удалось разлаживать логарифмические функции в степенной ряд.
Кроме этого, Эйлер применял логарифмы в работе с отрицательными и комплексными числами. В результате, он существенно расширил область использования логарифмов.
Затем ученый нашел уникальный способ решения квадратных уравнений. Он разработал новаторскую технику расчета интегралов, задействуя сложные пределы.
Кроме этого Эйлер вывел формулу вариационного исчисления, которая сегодня известна под названием – «уравнение Эйлера-Лагранжа».
Теория чисел
Леонард доказал малую теорему Ферма, тождества Ньютона, теорему Ферма о суммах 2-х квадратов, а также усовершенствовал доказательство теоремы Лагранжа о сумме 4-х квадратов.
Он также привнес важные дополнения в теорию совершенных чисел, которая волновала многих математиков того времени.
Физика и астрономия
Эйлер разработал способ решения уравнения «пучка Эйлера-Бернулли», которое затем начали активно использовать в инженерных вычислениях.
За свои заслуги в сфере астрономии Леонард удостоился многих престижных наград от Парижской академии. Он провел точные расчеты параллакса Солнца, а также с высокой точностью определил орбиты комет и прочих небесных тел.
Вычисления ученого помогли составить сверхточные таблицы небесных координат.
Биография Леонарда Эйлера
За время существования Академии наук в России, видимо, одним из самых знаменитых ее членов был математик Леонард Эйлер.
Он стал первым, кто в своих работах стал возводить последовательное здание анализа бесконечно малых. Только после его исследований, изложенных в грандиозных томах его трилогии «Введение в анализ», «Дифференциальное исчисление» и «Интегральное исчисление», анализ стал вполне оформившейся наукой — одним из самых глубоких научных достижений человечества.
Леонард Эйлер родился в швейцарском городе Базеле 15 апреля 1707 года. Отец его, Павел Эйлер, был пастором в Рихене (близ Базеля) и имел некоторые познания в математике. Отец предназначал своего сына к духовной карьере, но сам, интересуясь математикой, преподавал ее и сыну, надеясь, что она ему впоследствии пригодится в качестве интересного и полезного занятия. По окончанию домашнего обучения тринадцатилетний Леонард был отправлен отцом в Базель для слушания философии.
Портрет, выполненный Я. Э. Хандманном (1756)
Среди других предметов на этом факультете изучались элементарная математика и астрономия, которые преподавал Иоганн Бернулли. Вскоре Бернулли заметил талантливость юного слушателя и начал заниматься с ним отдельно.
Получив в 1723 году степень магистра, после произнесения речи на латинском языке о философии Декарта и Ньютона, Леонард, по желанию своего отца, приступил к изучению восточных языков и богословия. Но его все больше влекло к математике. Эйлер стал бывать в доме своего учителя, и между ним и сыновьями Иоганна Бернулли — Николаем и Даниилом — возникла дружба, сыгравшая очень большую роль в жизни Эйлера.
В 1725 году братья Бернулли были приглашены в члены петербургской академии наук, недавно основанной императрицей Екатериной I. Уезжая, Бернулли обещали Леонарду известить его, если найдется и для него подходящее занятие в России. На следующий год они сообщили, что для Эйлера найдется место, но, однако, в качестве физиолога при медицинском отделении академии. Узнав об этом, Леонард немедленно записался в студенты медицины Базельского университета. Прилежно и успешно изучая науки медицинского факультета, Эйлер находит время и для математических занятий. За это время он написал напечатанную потом в 1727 году в Базеле диссертацию о распространении звука и исследование по вопросу о размещении мачт на корабле.
В Петербурге имелись самые благоприятные условия для расцвета гения Эйлера материальная обеспеченность, возможность заниматься любимым делом, наличие ежегодного журнала для публикации трудов. Здесь же работала самая большая тогда в мире группа специалистов в области математических наук, в которую входили Даниил Бернулли (его брат Николай скончался в 1726 году), разносторонний X. Гольдбах, с которым Эйлера связывали общие интересы к теории чисел и другим вопросам, автор работ по тригонометрии Ф. X. Майера, астроном и географ Ж. Н. Делиль, математик и физик Г. В. Крафт и другие. С этого времени Петербургская Академия стала одним из главных центров математики в мире.
Базельский университет в XVII—XVIII веках
Открытия Эйлера, которые благодаря его оживленной переписке нередко становились известными задолго до издания, делают его имя все более широко известным. Улучшается его положение в Академии наук в 1727 году он начал работу в звании адъюнкта, то есть младшего по рангу академика, а в 1731 году он стал профессором физики, т. е. действительным членом Академии. В 1733 году получил кафедру высшей математики, которую до него занимал Д. Бернулли, возвратившийся в этом году в Базель. Рост авторитета Эйлера нашел своеобразное отражение в письмах к нему его учителя Иоганна Бернулли. В 1728 году Бернулли обращается к «ученейшему и даровитейшему юному мужу Леонарду Эйлеру», в 1737 году — к «знаменитейшему и остроумнейшему математику», а в 1745 году — к «несравненному Леонарду Эйлеру — главе математиков».
В 1735 году академии потребовалось выполнить весьма сложную работу по расчету траектории кометы. По мнению академиков, на это нужно было употребить несколько месяцев труда. Эйлер взялся выполнить это в три дня и исполнил работу, но вследствие этого заболел нервною горячкою с воспалением правого глаза, которого он и лишился. Вскоре после этого, в 1736 году, появились два тома его аналитической механики. Потребность в этой книге была большая; немало было написано статей по разным вопросам механики, но хорошего трактата по механике не имелось.
В 1738 году появились две части введения в арифметику на немецком языке, в 1739 году — новая теория музыки. Затем в 1840 году Эйлер написал сочинение о приливах и отливах морей, увенчанное одной третью премии французской академии; две других трети были присуждены Даниилу Бернулли и Маклорену за сочинения на ту же тему.
Гравюра В. П. Соколова (1766), вероятно по рисунку 1737 г.
В конце 1740 года власть в России попала в руки регентши Анны Леопольдовны и ее окружения. В столице сложилась тревожная обстановка. В это время прусский король Фридрих II задумал возродить основанное еще Лейбницем Общество наук в Берлине, долгие годы почти бездействовавшее. Через своего посла в Петербурге король пригласил Эйлера в Берлин. Эйлер, считая, что «положение начало представляться довольно неуверенным», приглашение принял.
В Берлине Эйлер поначалу собрал около себя небольшое ученое общество, а затем был приглашен в состав вновь восстановленной королевской академии наук и назначен деканом математического отделения. В 1743 году он издал пять своих мемуаров, из них четыре по математике. Один из этих трудов замечателен в двух отношениях. В нем указывается на способ интегрирования рациональных дробей путем разложения их на частные дроби и, кроме того, излагается обычный теперь способ интегрирования линейных обыкновенных уравнений высшего порядка с постоянными коэффициентами.
Вообще большинство работ Эйлера посвящено анализу. Эйлер так упростил и дополнил целые большие отделы анализа бесконечно малых, интегрирования функций, теории рядов, дифференциальных уравнений, начатые уже до него, что они приобрели примерно ту форму, которая за ними в большой мере сохраняется и до сих пор. Эйлер, кроме того, начал целую новую главу анализа — вариационное исчисление. Это его начинание вскоре подхватил Лагранж, и таким образом сложилась новая наука.
История жизни Леонарда Эйлера
В 1744 году Эйлером напечатал в Берлине три сочинения о движении светил, первое — теория движения планет и комет, заключающая в себе изложение способа определения орбит из нескольких наблюдений; второе и третье — о движении комет.
Семьдесят пять работ Эйлер посвятил геометрии. Часть из них хотя и любопытна, но не очень важна. Некоторые же просто составили эпоху. Во-первых, Эйлера надо считать одним из зачинателей исследований по геометрии в пространстве вообще. Он первый дал связное изложение аналитической геометрии в пространстве (во «Введении в анализ») и, в частности, ввел так называемые углы Эйлера, позволяющие изучать повороты тела вокруг точки.
В работе 1752 года «Доказательство некоторых замечательных свойств, которым подчинены тела, ограниченные плоскими гранями», Эйлер нашел соотношение между числом вершин, ребер и граней многогранника сумма числа вершин и граней равна числу ребер плюс два. Такое соотношение предполагал еще Декарт, но Эйлер доказал его в своих мемуарах. Это в некотором смысле первая в истории математики крупная теорема топологии — самой глубокой части геометрии.
Портрет 1756 года, выполненный Эмануэлем Хандманном (Kunstmuseum, г. Базель)
Занимаясь вопросами о преломлении лучей света и написав немало мемуаров об этом предмете, Эйлер издал в 1762 году сочинение, в котором предлагается устройство сложных объективов с целью уменьшения хроматической аберрации. Английский художник Долдонд, открывший два различной преломляемости сорта стекла, следуя указаниям Эйлера, построил первые ахроматические объективы.
В 1765 году Эйлер написал сочинение, где решает дифференциальные уравнения вращения твердого тела, которые носят название Эйлеровых уравнений вращения твердого тела.
Много написал ученый сочинений об изгибе и колебании упругих стержней. Вопросы эта интересны не только в математическом, но и в практическом отношении.
Фридрих Великий давал ученому поручения чисто инженерного характера. Так, в 1749 году он поручил ему осмотреть канал Фуно между Гавелем и Одером и дать рекомендации по исправлению недостатков этого водного пути. Далее ему поручено было исправить водоснабжение в Сан-Суси.
Результатом этого стало более двадцати мемуаров по гидравлике, написанных Эйлером в разное время. Уравнения гидродинамики первого порядка с частными производными от проекций скорости, плотности к давлению называются гидродинамическими уравнениями Эйлера.
Покинув Петербург, Эйлер сохранил самую тесную связь с русской Академией наук, в том числе официальную он был назначен почетным членом, и ему была определена крупная ежегодная пенсия, а он, со своей стороны, взял на себя обязательства в отношении дальнейшего сотрудничества. Он закупал для нашей Академии книги, физические и астрономические приборы, подбирал в других странах сотрудников, сообщая подробнейшие характеристики возможных кандидатов, редактировал математический отдел академических записок, выступал как арбитр в научных спорах между петербургскими учеными, присылал темы для научных конкурсов, а также информацию о новых научных открытиях и т. д. В доме Эйлера в Берлине жили студенты из России М. Софронов, С. Котельников, С. Румовский, последние позднее стали академиками.
Фридрих II Прусский
Из Берлина Эйлер, в частности, вел переписку с Ломоносовым, в творчестве которого он высоко ценил счастливое сочетание теории с экспериментом. В 1747 году он дал блестящий отзыв о присланных ему на заключение статьях Ломоносова по физике и химии, чем немало разочаровал влиятельного академического чиновника Шумахера, крайне враждебно относившегося к Ломоносову.
В переписке Эйлера с его другом академиком Петербургской Академии наук Гольдбахом мы находим две знаменитые «задачи Гольдбаха» доказать, что всякое нечетное натуральное число есть сумма трех простых чисел, а всякое четное — двух. Первое из этих утверждений было при помощи весьма замечательного метода доказано уже в наше время (1937 год) академиком И. М. Виноградовым, а второе не доказано до сих пор.
Эйлера тянуло назад в Россию. В 1766 году он получил через посла в Берлине, князя Долгорукова, приглашение императрицы Екатерины II вернуться в академию наук на любых условиях. Несмотря на уговоры остаться, он принял приглашение и в июне прибыл в Петербург.
Императрица предоставила Эйлеру средства на покупку дома. Старший из его сыновей Иоганн Альбрехт стал академиком по физике, Карл занял высокую должность в медицинском ведомстве; Христофора, родившегося в Берлине, Фридрих II долго не отпускал с военной службы, и потребовалось вмешательство Екатерины II, чтобы тот смог приехать к отцу. Христофор был назначен директором Сестрорецкого оружейного завода.
Еще в 1738 году Эйлер ослеп на один глаз, а в 1771-м после операции почти совсем потерял зрение и мог писать только мелом на черной доске, но благодаря ученикам и помощникам И.А. Эйлеру, А.И. Локселю, В.Л. Крафту, С.К. Котельникову, М.Е. Головину, а главное Н.И. Фуссу, прибывшему из Базеля, продолжал работать не менее интенсивно, чем раньше.
Здание Петербургской Академии наук во второй половине XVIII века (Кунсткамера)
Эйлер, при своих гениальных способностях и замечательной памяти, продолжал работать, диктовать свои новые мемуары. Только с 1769 по 1783 годы Эйлер продиктовал около 380 статей и сочинений, а за свою жизнь написал около 900 научных работ.
Работа 1769 года «Об ортогональных траекториях» Эйлера содержит блестящие соображения о получении с помощью функции комплексной переменной из уравнений двух взаимно ортогональных семейств кривых на поверхности (т. е. таких линий, как меридианы и параллели на сфере) бесконечного числа других взаимно ортогональных семейств. Работа эта в истории математики оказалась очень важной.
В следующей работе 1771 года «О телах, поверхность которых может быть развернута в плоскость» Эйлер доказывает знаменитую теорему о том, что любая поверхность, которую можно получить, лишь изгибая плоскость, но не растягивая ее и не сжимая, если она не коническая и не цилиндрическая, представляет собой совокупность касательных к некоторой пространственной кривой.
Столь же замечательны работы Эйлера по картографическим проекциям.
Можно себе представить, каким откровением для математиков той эпохи явились хотя бы работы Эйлера о кривизне поверхностей и о развертывающихся поверхностях. Работы же, в которых Эйлер исследует отображения поверхности, сохраняющие подобие в малом (конформные отображения), основанные на теории функций комплексного переменного, должны были казаться прямо-таки трансцендентными. А работа о многогранниках начинала совсем новую часть геометрии и по своей принципиальности и глубине стояла в ряду с открытиями Евклида.
Неутомимость и настойчивость в научных исследованиях Эйлера были таковы, что в 1773 году, когда сгорел его дом и погибло почти все имущество его семейства, он и после этого несчастья продолжал диктовать свои исследования. Вскоре после пожара искусный окулист, барон Вентцель, произвел операцию снятия катаракты, но Эйлер не выдержал надлежащего времени без чтения и ослеп окончательно.
«Письма к немецкой принцессе», третье издание (1780)
В том же 1773 году умерла жена Эйлера, с которой он прожил сорок лет. Через три года он вступил в брак с ее сестрой, Саломеей Гзелль. Завидное здоровье и счастливый характер помогали Эйлеру «противостоять ударам судьбы, которые выпали на его долю. Всегда ровное настроение, мягкая и естественная бодрость, какая-то добродушная насмешливость, умение наивно и забавно рассказывать делали разговор с ним столь же приятным, сколь и желанным. » Он мог иногда вспылить, но «был не способен долго питать против кого-либо злобу. » — вспоминал Н.И. Фусс.
Эйлера постоянно окружали многочисленные внуки, часто на руках у него сидел ребенок, а на шее лежала кошка. Он сам занимался с детьми математикой. И все это не мешало ему работать!
18 сентября 1783 года Эйлер скончался от апоплексического удара в присутствии своих помощников профессоров Крафта и Лекселя. Он был похоронен на Смоленском лютеранском кладбище. Академия заказала известному скульптору Ж.Д. Рашетту, хорошо знавшему Эйлера, мраморный бюст покойного, а княгиня Дашкова подарила мраморный пьедестал.
До конца XVIII века конференц-секретарем академии оставался И.А. Эйлер, которого сменил Н.И. Фусс, женившийся на дочери последнего, а в 1826 году — сын Фусса Павел Николаевич, так что организационной стороной жизни Академии около ста лет ведали потомки Леонарда Эйлера. Эйлеровские традиции оказали сильное влияние и на учеников Чебышева А.М. Ляпунова, А.Н. Коркина, Е.И. Золотарева, А.А. Маркова и других, определив основные черты петербургской математической школы.
Нет ученого, имя которого упоминалось бы в учебной математической литературе столь же часто, как имя Эйлера. Даже в средней школе логарифмы и тригонометрию изучают до сих пор в значительной степени «по Эйлеру».
Эйлер нашел доказательства всех теорем Ферма, показал неверность одной из них, а знаменитую Великую теорему Ферма доказал для «трех» и «четырех». Он также доказал, что всякое простое число вида 4п+1 всегда разлагается на сумму квадратов других двух чисел. Эйлер начал последовательно строить элементарную теорию чисел. Начав с теории степенных вычетов, он затем занялся квадратичными вычетами. Это так называемый квадратичный закон взаимности. Эйлер также много лет занимался решением неопределенных уравнений второй степени с двумя неизвестными.
Надгробие Л. Эйлера, гранитный саркофаг
Во всех этих трех фундаментальных вопросах, которые больше двух столетий после Эйлера и составляли основной объем элементарной теории чисел, ученый ушел очень далеко, однако во всех трех его постигла неудача. Полное доказательство получили Гаусс и Лагранж.
Эйлеру принадлежит инициатива создания и второй части теории чисел — аналитической теории чисел, в которой глубочайшие тайны целых чисел, например, распределение простых чисел в ряду всех натуральных чисел, получаются из рассмотрения свойств некоторых аналитических функций.
Созданная Эйлером аналитическая теория чисел продолжает развиваться и в наши дни.