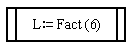линейные алгоритмы что такое
Линейный алгоритм и как решать задачи: подборка примеров, детальное описание
Содержание:
Каждый линейный алгоритмический конструктив включает базовые структуры. К простейшим базовым принципам относят принцип следования, имеющий линейные характеристики. На основании этого информатика дает точное определение.
Линейная конструкция является алгоритмом из группы команд. Следование командам – однократное, последовательное. Простая структура может быть выражена в виде графика или текстового описания.
Как сформировать алгоритм: порядок действий
Чтобы получилась целостная конструкция, нужно выполнить следующие шаги:
В итоговой блок-схеме важно указать процесс ввода, вывода сведений, полный список всех вычислительных операций.
Дан фрагмент линейного алгоритма a 8 – как решить задачу
В задаче дан фрагмент линейного алгоритма а 8, при этом б : = 6 + 3а, а : = б : 3а. Нужно вычислить переменную после решения системы.
Коэффициент а инициализируется при первичном вводе, его установленное значение 8 является целым. Так как изначально дан фрагмент линейного алгоритма с переменной б, она также используется для выделения измененного следующего показателя. Чтобы установить изменение а, необходимо предварительно вычислить значение б. Для этого:
б = 6 + 3 × 8 = 6 + 24 = 30
Пока число а не изменилось, оно равняется 8. Формируется дробное выражение с 8 в знаменателе: а = 30 : 3 × 8 = 10 × 8 = 80
Итог: когда код исполнится, переменная станет равна 80.
Блок-схема простейшего линейного алгоритма
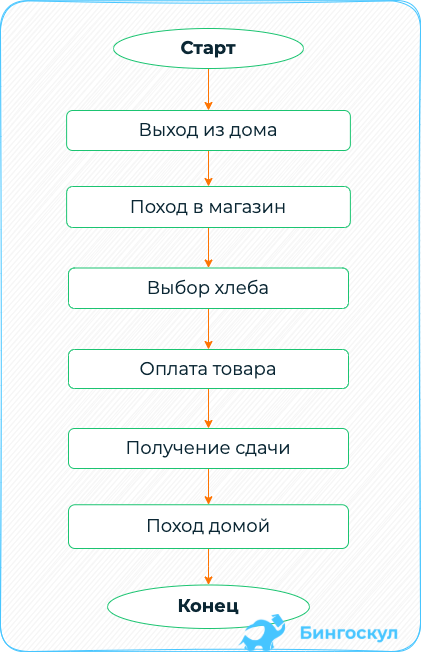
Рассмотрим принцип линейных выражений на простом примере из жизни. Необходимо построить алгоритм покупки хлеба. В текстовой форме он будет иметь вид:
Графическое представление выглядит следующим образом:
Решение задачи по алгоритму «Узор»
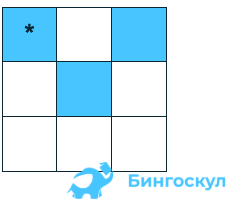
Робот владеет четырьмя командами: перемещается вправо, влево, вниз, вверх. Каждый ход – одна клетка в указанном направлении. Команда «Закрасить» заставляет исполнителя зарисовывать клетки, в которых он пребывает в данный момент. Нужно составить алгоритмическую структуру закрашивания двух угловых верхних клеток, одной средней, возврата в угловую верхнюю клетку. Точка возврата отмечена на рисунке *.
Линейные алгоритмы что такое
Понятие алгоритма. Исполнитель алгоритма. Свойства алгоритма. Способы записи алгоритмов.
Основные алгоритмические структуры: следование, ветвление, цикл; изображение
на блок-схемах. Вспомогательные алгоритмы.
Алгоритм – описание последовательности действий (план), строгое исполнение которых приводит к решению поставленной задачи за конечное число шагов.
Вы постоянно сталкиваетесь с этим понятием в различных сферах деятельности человека (кулинарные книги, инструкции по использованию различных приборов, правила решения математических задач. ). Обычно мы выполняем привычные действия не задумываясь, механически. Например, вы хорошо знаете, как открывать ключом дверь. Однако, чтобы научить этому малыша, придется четко разъяснить и сами эти действия и порядок их выполнения:
1. Достать ключ из кармана.
2. Вставить ключ в замочную скважину.
3. Повернуть ключ два раза против часовой стрелки.
Если вы внимательно оглянитесь вокруг, то обнаружите множество алгоритмов которые мы с вами постоянно выполняем. Мир алгоритмов очень разнообразен. Несмотря на это, удается выделить общие свойства, которыми обладает любой алгоритм.
Дискретность (от лат. discretus — разделённый, прерывистый, раздельность) (алгоритм должен состоять из конкретных действий, следующих в определенном порядке);
Детерминированность (от. лат. determinate – определенность, точность) (любое действие должно быть строго и недвусмысленно определено в каждом случае);
Конечность (каждое действие и алгоритм в целом должны иметь возможность завершения);
Массовость (один и тот же алгоритм можно использовать с разными исходными данными);
Результативность (отсутствие ошибок, алгоритм должен приводить к правильному результату для всех допустимых входных значениях).
1. Линейный алгоритм (описание действий, которые выполняются однократно в заданном порядке);
2. Циклический алгоритм (описание действий, которые должны повторятся указанное число раз или пока не выполнено заданное условие);
3. Разветвляющийся алгоритм (алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий);
4. Вспомогательный алгоритм (алгоритм, который можно использовать в других алгоритмах, указав только его имя).
На практике наиболее распространены следующие формы представления алгоритмов:
В письменной форме на естественном языке.
В письменной форме на формальном языке.
Для более наглядного представления алгоритма широко используется графическая форма – блок-схема, которая составляется из стандартных графических объектов.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура.
Стадии создания алгоритма:
1. Алгоритм должен быть представлен в форме, понятной человеку, который его разрабатывает (определить цель, наметить план действий).
2. Алгоритм должен быть представлен в форме, понятной тому объекту (в том числе и человеку), который будет выполнять описанные в алгоритме действия (выбрать среду и объект алгоритма, детализировать алгоритм).
Объект, который будет выполнять алгоритм, обычно называют исполнителем.
Назначение исполнителя точно выполнить предписания алгоритма, подчас не задумываясь о результате и целях, т.е. формально. Идеальными исполнителями являются машины, роботы, компьютеры.
Компьютер – автоматический исполнитель алгоритмов.
Алгоритм, записанный на «понятном» компьютеру языке программирования, называется программой.
Линейный алгоритм
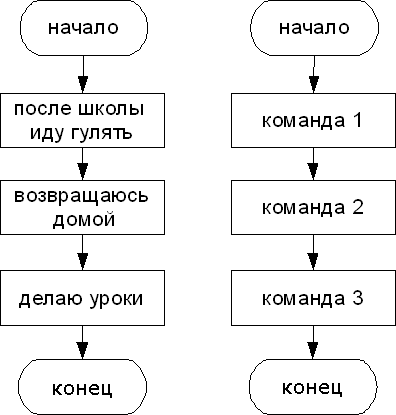
Линейный алгоритм – описание действий, которые выполняются однократно в заданном порядке. Исполнитель выполняет действия последовательно, одно за другим в том порядке в котором они следуют.
Блок-схема линейного алгоритма:
Циклический алгоритм – описание действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие.
Перечень повторяющихся действий называют телом цикла.
Циклические алгоритмы бывают двух типов:
Циклы со счетчиком, в которых какие-то действия выполняются определенное число раз;
Циклы с условием, в которых тело цикла выполняется, в зависимости от какого-либо условия. Различают циклы с предусловием и постусловием.
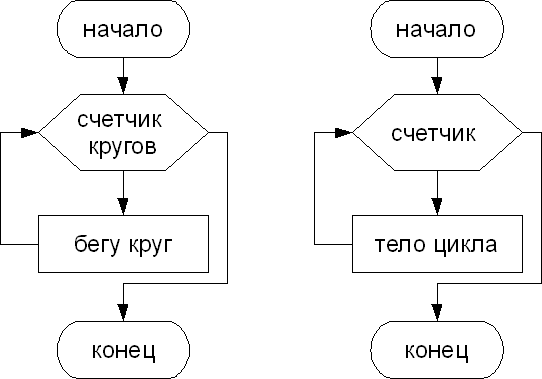
Циклы со счетчиком используют когда заранее известно какое число повторений тела цикла необходимо выполнить. Например, на уроке физкультуры вы должны пробежать некоторое количество кругов вокруг стадиона.
Для счетчика от нач. значения до кон. значения выполнить действие.
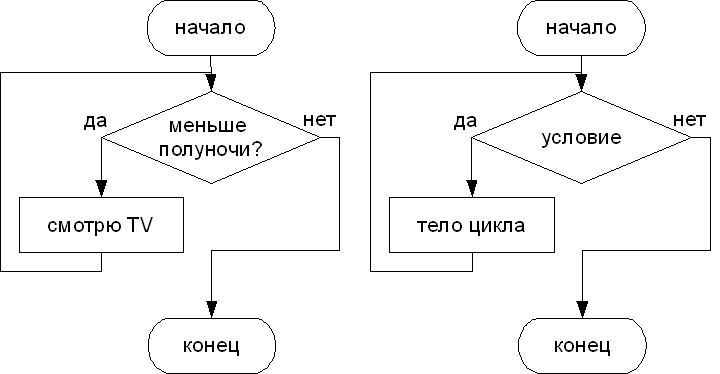
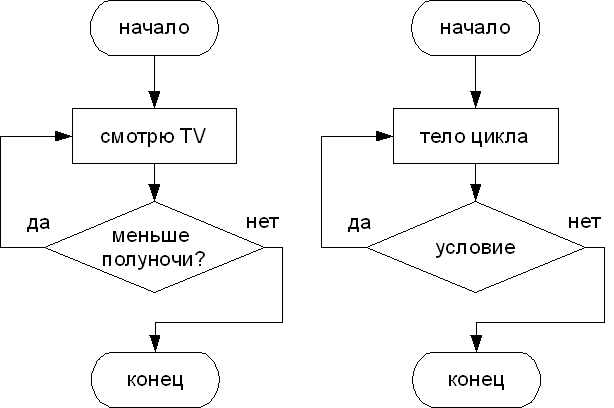
Часто бывает так, что необходимо повторить тело цикла, но заранее не известно, какое количество раз это надо сделать. В таких случаях количество повторений зависит от некоторого условия. Такие циклы называются циклы с условием. Циклы в которых сначала проверяется условие, а затем, возможно, выполняется тело цикла называют циклы с предусловием. Если условие проверяется после первого выполнения тела цикла, то циклы называются циклы с постусловием.
Например, в субботу вечером вы смотрите телевизор. Время от времени поглядываете на часы и если время меньше полуночи, то продолжаете смотреть телевизор, если это не так, то вы прекращаете просмотр телепередач.
В общем случае схема циклического алгоритма с условием будет выглядеть так:
Пока условие повторять действие.
При составлении циклических алгоритмов важно думать о том, чтобы цикл был конечным. Ситуация, при которой выполнение цикла никогда не заканчивается, называется зацикливанием.
Во многих случаях требуется, чтобы при одних условиях выполнялась одна последовательность действий, а при других – другая.
Если пошел дождь, то надо открыть зонт.
Если прозвенел будильник, то надо вставать.
Если встречу Сашу, то скажу ему …
Если встречу Сашу, то скажу ему …, иначе зайду к нему сам.
Эти предложения начинаются с проверки какого-либо условия: пошел дождь, прозвенел будильник, встретил Сашу… Далее в зависимости мы либо вылиняем какое-либо действие, либо не выполняем его (или выполняем какое-то другое действие).
Компьютер тоже в зависимости от какого-либо условия может выполнять или не выполнять те или иные действия. Алгоритм, в котором используется условие, получил название разветвляющегося, так как в зависимости от значения условия выбираются те или иные действия.
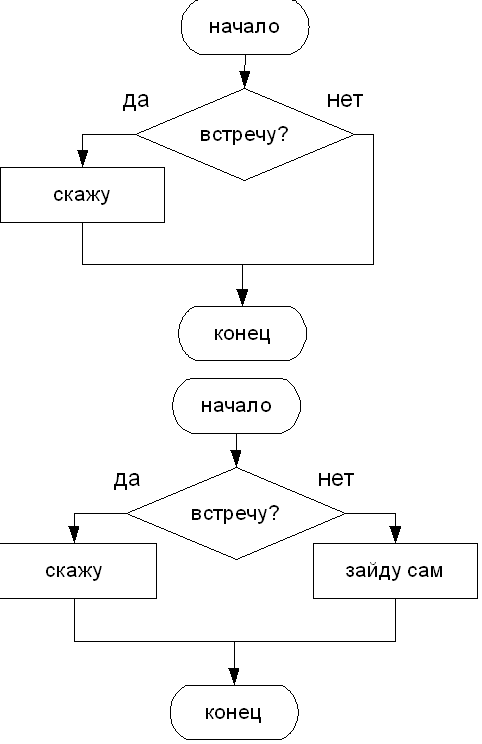
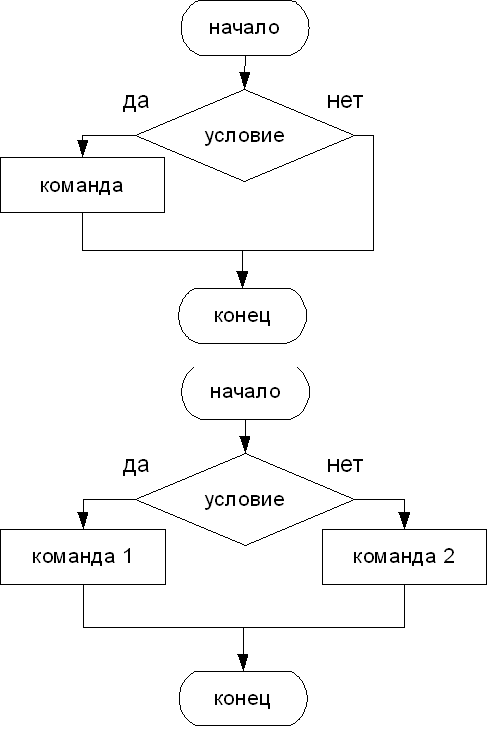
В общем случае схема разветвляющегося алгоритма будет выглядеть так: «если условие, то действие 1, иначе действие 2» (Если встречу Сашу, то скажу ему …, иначе зайду к нему сам.). Так же можно использовать неполную форму: «если условие, то действие» (Если встречу Сашу, то скажу ему ). В этом случае не предусматривается действий на случай невыполнения условия.
Условие – это высказывание которое может быть либо истинно, либо ложно.
Еще раз обратим внимание, что существует две формы ветвления – неполная (когда присутствует только одна ветвь, т.е. в зависимости от истинности условия либо выполняется, либо не выполняется действие) и полная (когда присутствуют две ветви, т.е. в зависимости от истинности условия выполняется либо одно, либо другое действие).
Вспомогательный алгоритм – алгоритм, который можно использовать в других алгоритмах, указав только его имя.
Линейный алгоритм. Понятие и особенности. Блок-схема
Каждый человек на протяжении своей жизни решает множество задач разной сложности. Но даже самые простые из задач выполняются последовательно, то есть за несколько шагов. Эту последовательность можно назвать алгоритмом. Последовательности бывают разные, но начинать их изучение лучше всего с линейных.
Прежде чем приступить к рассмотрению основной темы статьи, следует сделать краткое отступление и сказать несколько слов про алгоритмический язык.
Алгоритмический язык
Представьте, что человеку, работающему за компьютером, поставлена некая вычислительная задача. В языке программирования решение этой задачи выполняется с помощью алгоритмизации. Решение предполагает: — разбиение на этапы; — разработку алгоритма; — составление программы решения на алгоритмическом языке; — ввод данных; — отладку программы (возможны ошибки — их надо исправить); — выполнение на ПК; — анализ результатов.
Алгоритмический язык является средством описания алгоритмов, а уже алгоритм, в свою очередь, представляет собой чёткое описание определённой последовательности действий, направленных на решение необходимой задачи.
Свойства алгоритма
Их несколько: — конечность. Любой алгоритм должен быть завершённым, а окончание наступает после выполнения определённого числа шагов; — однозначность, понятность. Не допускается разных толкований, неопределённости и двусмысленности — всё должно быть чётко и ясно, а также понятно исполнителю — и правила выполнения действий линейного алгоритма, и сами действия; — результативность. Итог работы — результат, полученный за конечное число шагов; — универсальность, массовость. Качественный алгоритм способен решать не одну задачу, а целый класс задач, имеющих схожую постановку/структуру.
Линейная структура
Любой алгоритм составляется из ряда базовых структур. Простейшей базовой структурой является следование — структура с линейными характеристиками. Из этого можно сформулировать определение.
Линейный алгоритм — это алгоритм, образуемый командами, которые выполняются однократно и именно в той последовательности, в которой записаны. Линейная структура, по сути, проста. Записать её можно как в текстовой, так и в графической форме.
Представим, что у нас стоит задача пропылесосить ковёр в комнате. В текстовой форме алгоритм будет следующим: — принести пылесос к месту уборки; — включить; — пропылесосить; — выключить; — унести пылесос.
И каждый раз, когда нам надо будет пылесосить, мы будем выполнять один и тот же алгоритм.
Теперь поговорим про графическую форму представления.
Блок-схема
Для изображения алгоритма графически используют блок-схемы. Они представляют собой геометрические фигуры (блоки), соединённые стрелками. Стрелки показывают связь между этапами и последовательность их выполнения. Каждый блок сопровождается надписью.
Рассмотрим фигуры, которые используются при визуализации типичной линейной последовательности.
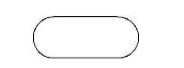
Блок ввода-вывода данных (отображает список вводимых и выводимых переменных):
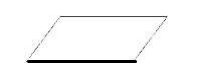
Арифметический блок (отображает арифметическую операцию/группу операций):
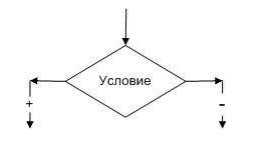
Условный блок (позволяет описать условие). Алгоритмы с таким блоком используются при графической визуализации алгоритмов с ветвлением:
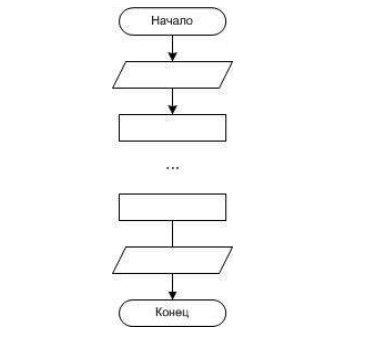
Условного блока нет в классическом линейном алгоритме, так как в нём, как уже было сказано ранее, все операции выполняются последовательно, то есть одна за другой. В линейном алгоритме размещение блоков выглядит следующим образом:
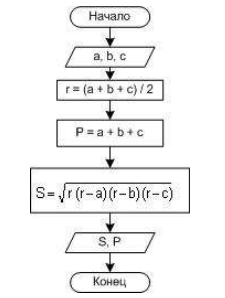
А вот, как решается задача по нахождению площади треугольника по формуле Герона. Здесь a, b, c – это длины сторон, S – площадь треугольника, P – периметр.
Следует обратить внимание, что запись «=» — это не математическое равенство, а операция присваивания. В результате этой операции переменная, стоящая слева от оператора, получает значение, которое указано справа. Значение не обязательно должно быть сразу определено (a = 3) — оно может вычисляться посредством выражения (a = b + z), где b = 1, a z = 2.
Примеры линейных алгоритмов
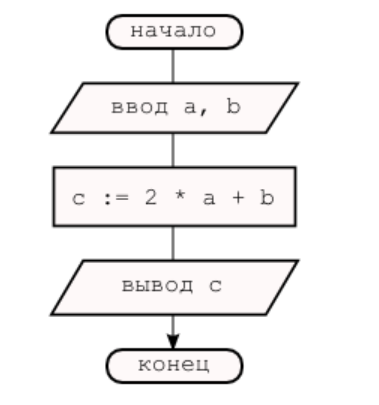
Если рассмотреть примеры решения на языке Pascal (именно этот язык до сих пор используется для изучения основ алгоритмизации и программирования), то можно увидеть следующую картину:
И, соответственно, блок-схема программы линейной структуры будет выглядеть следующим образом:
Как составить программу линейной структуры?
Порядок следующий: — определите, что именно относится к исходным данными, а также каков типы/класс этих данных, выберите имена переменных; — определите, каков тип данных будет у искомого результата, выберите название переменных (переменной); — определите, какие математические формулы связывают результат и исходные данные; — если требуется наличие промежуточных данных, определите класс/типы этих данных и выберите имена; — опишите все используемые переменные; — запишите окончательный алгоритм. Он должен включать в себя ввод данных, вычисления, вывод результатов.
На этом всё, в следующий раз рассмотрим на примерах программу разветвлённой структуры. Если же вас интересует тема алгоритмизации в контексте разработки программного обеспечения, ждём вас на профессиональном курсе OTUS!
Линейные алгоритмы что такое
Пособие представляют собой руководство по составлении алгоритмов, которые являются необходимой составной частью контрольной и курсовой работы по дисциплине «Информатика».
Изложенный материал не претендует на полноту охвата всех сторон проблемы алгоритмизации при решении задач, возникающих на практике. Однако его вполне достаточно для того, чтобы разобраться и выполнить ту часть названных работ, которая необходима для составления алгоритмов и их описания.
Опыт показывает, что трудности, возникающие при составлении алгоритмов имеют как общий характер, когда студент не может уяснить принцип работы алгоритма вообще, так и частный, когда непонятным оказывается отдельный фрагмент алгоритма.
В любом случае рекомендуем обратить внимание на следующее. Разбирая или составляя алгоритм, нужно мысленно представить некоторый автомат по обработке данных (компьютер), который будет выполнять действия, предписанные этим алгоритмом. Без такого представления невозможно понять сам алгоритм. Ниже, при разборе примеров, станет понятно, что такой мысленный автомат совсем несложен. Во всяком случае он несравнимо пpoщe реального компьютера, хотя общие принципы их функционирования в основном одинаковы. Допустимо (например, при составлении описания) отождествлять работу такого автомата с работой самого алгоритма.
При изучении материала особенно первоначальном, следует подробно разобраться в каждом алгоритме, начиная с самого первого и самого простого. Начинать нужно с полного уяснения пяти самых простых и самых необходимая понятий: константа, переменная, ячейка памяти, запись константы в ячейку памяти, чтение константы из ячейки памяти. Не пренебрегайте этими советами, так как очень скоро убедитесь, что при разборе следующего алгоритма обязательно натолкнетесь не только на те же трудности, но присовокупите к ним новые. Более того, нередко полное понимание даже самого простого алгоритма дает намного больше пользы, чем поверхностное изучение десятка алгоритмов повышенной сложности.
Алгоритм – это инструкция для автомата о том, в какой последовательности нужно выполнить действия при переработке исходного материала в требуемый результат.
Наряду с понятием алгоритма используют термин алгоритмизация, под которой понимают совокупность приемов и способов составления алгоритмов для решения алгоритмических задач.
Часто алгоритм используется не как инструкция для автомата, а как схема алгоритмического решения задачи. Это позволяет оценить эффективность предлагаемого способа решения, его результативность, исправить возможные ошибки, сравнить его еще до применения на компьютере с другими алгоритмами решения этой же задачи. Наконец, алгоритм является основой для составления программы, которую пишет программист на каком-либо языке программирования с тем, чтобы реализовать процесс обработки данных на компьютере.
Неотъемлемым свойством алгоритма является его результативность, то есть алгоритмическая инструкция лишь тогда может быть названа алгоритмом, когда при любом сочетании исходных данных она гарантирует, что через конечное число шагов будет обязательно получен результат.
На практике получили известность два способа изображения алгоритмов:
в виде пошагового словесного описания;
Первый из этих способов получил значительно меньшее распространение из-за его многословности и отсутствия наглядности.
Второй, напротив, оказался очень удобным средством изображения алгоритмов и получил широкое распространение в научной и учебной литературе. Именно этот способ будет использован ниже при составлении и описании алгоритмов.
Блок-схема – это совокупность блоков, предписывающих выполнение определенных операций, и связей между этими блоками. Внутри блоков указывается информация об операциях, подлежащих выполнению. Конфигурация и размеры блоков, а также порядок графического оформления блок-схем регламентированы ГОСТ 19.701-90 (ИСО 5807-85) «Единая система программной документации. СХЕМЫ АЛГОРИТМОВ, ПРОГРАММ, ДАННЫХ И СИСТЕМ. Условные обозначения и правила выполнения» [1]. В табл. 1 приведены наиболее часто используемые блоки, изображены элементы связей между ними и дано краткое пояснение к ним. Блоки и элементы связей называют символами блок-схем. Представленных в таблице символов вполне достаточно для изображения алгоритмов, которые необходимы при выполнении студенческих работ.
Таблица 1
О тображает выход во внешнюю среду и вход из внешней среды (начало или конец схемы программы, алгоритма).
Вычислительное действие или последовательность вычислительных действий
Проверка условияГраницы цикла

Нижняя границаПодготовка

Предопределенный процесс
О тображает процесс, состоящий из одной или нескольких операций или шагов программы, которые определены в другом месте (в подпрограмме, модуле)
О тображает данные, представленные на носителе в удобочитаемой форме.
Будет использоваться нами как символ вывода данных
О тображает данные, представленные на носителе в виде карты (перфокарты, магнитные карты и др.).
Будет использоваться нами как символ ввода данных
Может использоваться для ввода/вывода данных
Отображает выход в часть схемы и вход из другой части этой схемы и используется для обрыва линии и продолжения ее в другом месте
И спользуют для добавления описательных комментариев или пояснительных записей в целях объяснения или примечаний
Линии горизонтальных и вертикальных потоков, предназначенные для связей между символами
Слияние линий потоков
Межстраничный соединитель
При соединении блоков следует использовать вертикальные и горизонтальные линии потоков.
Горизонтальные потоки, имеющие направление справа налево, и вертикальные потоки, имеющие направление снизу вверх, должны быть обязательно помечены стрелками. Прочие потоки могут быть помечены или оставлены непомеченными.
Желательно чтобы линии потоков были параллельны линиям внешней рамки или границам листа.
Рекомендуется расстояние между параллельными линиями потоков устанавливать кратным 5 мм.
Горизонтальный и вертикальный размеры блока рекомендуется назначать кратно 5-ти мм.
Для размещения блоков рекомендуется поле листа разбивать на горизонтальные и вертикальные (для разветвлявшихся схем) зоны.
Для удобства описания блок-схемы каждый ее блок следует пронумеровать. Удобно использовать сквозную нумерации блоков. Номер блока располагают в разрыве в левой верхней части рамки блока или над ним.
По характеру связей между блоками различают алгоритмы линейной, разветвляющейся и циклической структуры.
Примеры, пояснявшие изложенное, можно найти в блок-схемах алгоритмов, которые будут приведены ниже.
Для того чтобы ясно представить как «работает» алгоритм, опишем простейший автомат, который предназначен для выполнения операций, предписанных этим алгоритмом.
В состав такого автомата входят:
Головка, получив указание от процессора, может записывать в ячейку или считывать из нее одну константу.
В простейшем случае константой является любое арифметическое число. Например, 12, 0.78, 0, –45.33 и т. д. ( Константами могут быть такие строки символов, структуры данных и др.).
Переменные имеют буквенно-символьное обозначение. Например, 1, n, a, a1, b, H2 – переменные. Одновременно обозначение переменной является индексом ячейки, в которую будут записываться константы. Любая из таких констант называется значением переменной. Например, Z является переменной и адресом ячейки Z одновременно. С алгоритмической точки зрения понятия “ переменная ” и “ адрес ячейки ” памяти являются идентичными.
Запись вида L = M следует понимать так: прочитать константу, расположенную по адресу M и скопировать эту константу в ячейку с адресом L (при этом константа из ячейки M не удаляется, а остается такой, какой она была до чтения). Произносить эту запись нужно так: «переменной L присвоить значение переменной M (или просто : L присвоить M)».
Одномерный массив – это последовательность ячеек, расположенных в одну линию. На рис. 1 приведен пример такого массива.
Рис. 1. Одномерный массив q
Рис.2. Двумерный массив d
Аналогично устроена структура массивов трех- и большей размерности.
Линейный алгоритм – это алгоритм, в котором блоки выполняются последовательно сверху вниз от начала до конца.
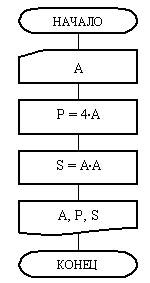
На рис. 3 приведен пример блок-схемы алгоритма вычисления периметра Р и площади S квадрата со стороной длины A.
Как видно из рис.3, блок 1 связан вертикальной линией потока с блоком 2. Эта линия не имеет стрелки, указывавшей направление потока. Следовательно, этот поток направлен вниз. Таким образом, после выполнения блока 1 управление будет передано на блок 2. Блок 2 «Перфокарта» ( см. табл. 1) показывает, что переменной A следует присвоить значение. Это означает, что в ячейку, отведенную автоматом под эту переменную, нужно поместить константу. На реальной компьютере эта константа может быть введена самыми разными способами. Способ зависит от того, как запрограммирован данный фрагмент. Можно, например, потребовать ввод константы с клавиатура или получить его из заранее подготовленного файла. Возможно эта константа будет получена через внешние источники данных, например, от физической установки, подключенной к компьютеру.
Рис. 3. Линейный алгоритм
Для данного примера способ передачи константы не имеет значения, важно лишь то, что при выполнении блока 2 в ячейку с адресом А будет занесена конкретная константа. Пусть такой константой является число 5.
Далее управление по линии потока передается к блоку 3 «Процесс». В этом блоке при выполнении размещенной в ней команды число 4 умножается на константу, помещенную в ячейку А (т. е. 5), и результат (т. е. 20) присваивается переменной Р (т. е. константа 20 записывается в ячейку по адресу Р). После выполнения этих операций управление передается к блоку 4.
В блоке 4 аналогичным образом производится умножение значений переменной А и результат (константа 25) присваивается переменной S (в ячейку по адресу S будет занесена константа 25). После этого выполняется переход к блоку 5.
При выполнении команд блока 5 выводятся (например, на экран, бумагу, во внешний файл и т. д.) значения переменных А, Р, S, которые сохранились в соответствующих ячейках к этому моменту. Понятно, что для конкретного примера А = 5 будут выведена константы 5, 20, 25, т. е. длина сторона квадрата, его периметр и площадь. Далее управление передается последнему блоку 6.
Понятно, что при новом запуске этого же алгоритма можно получить совсем другие числа. Так, если в блоке 2 переменной А присвоить значение 20, то алгоритм выдаст в блоке 5 константы 20, 80, 400.
Детальное описание алгоритма рис. 3 приведено для того, чтобы показать, в какой последовательности автомат выполняет предписанные операции и как при этом меняется состояние памяти автомата, т. е. для того, чтобы объяснить суть происходящих в автомате процессов. Из сказанного нужно уяснить, что автомат выполняет предписанную ему работу шаг за шагом. Всякий шаг обрабатывается процессором. Помимо вычислений процессор при необходимости отдает команды считывавшей/записывавшей головке, что и куда записывать, откуда читать. Конечный результат следует искать в ячейках памяти, каждая из которых до окончания алгоритма имеет известный адрес и хранит записанную в нее константу.
При выполнении контрольной или курсовой работы нет нужды давать столь подробное описание алгоритма. Тем не менее, описание должно быть выполнено с той степенью полноты, которая позволяет дать ясное представление о всех сторонах и особенностях алгоритмического процесса.
На практике алгоритмы линейной структуры встречается крайне редко. Чаще необходимо организовать процесс, который в зависимости от каких-либо условий проходит по той либо иной ветви алгоритма. Такой алгоритм называется разветвляющимся.
В блок-схемах ветвление начинается на выходах символа «Решение», с помощью которого в алгоритме выполняется проверка какого-либо условия. Количество ветвей тем больше, чем больше проверяемых условий.
Для пояснения рассмотрим решение задачи нахождения значения функции z = y/x.
На первый взгляд представляется, что алгоритм решения этой задачи имеет линейную структуру. Однако, если учесть, что делить на нуль нельзя из-за переполнения ячейки, то, во-первых, нужно из вычислений исключить вариант х = 0 и, во-вторых, проинформировать пользователя алгоритма о возникшей ошибке. Если этого не сделать, то при вычислениях может возникнуть аварийный выход до получения результата. В профессиональной практике аварийные завершения крайне нежелательны. т. к. к этому моменту уже может быть накоплено определенное количество результатов, которые окажутся необработанными и попросту пропадут. Можно привести другие примеры, когда аварийный останов компьютера может повлечь куда более серьезные последствия.
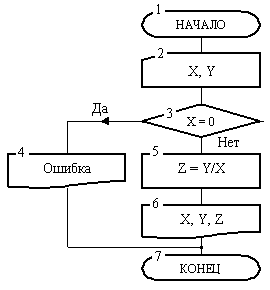
Решение задачи представлено блок-схемой рис. 4.
Она состоит из 7 блоков. После начала работы алгоритм в блоке 2 требует ввода аргументов X и Y. Затем в блоке 3 производится проверка условия X = 0. Здесь автомат проверяет равна ли нули константа, введенная в ячейку с адресом X. Результатом такой проверки является ответ «Да» или «Нет». В зависимости от этого ответа выполнение алгоритма пойдет по одной или другой ветви. Если результат проверки окажется отрицательным, то на х можно делить и управление передается блоку 4.
В блоке 4 будет получен результат Z, затем в блоке б значения всех трех переменных будут отпечатаны и в блоке 7 алгоритм закончит работу. Если же ответ окажется положительным, то управление будет передано блоку 4. Выполняя команду блока 4, автомат выведет сообщение «Ошибка» и затем закончит работу в том же блоке 7.
Часто при решении задач приходится повторять выполнение операций по одним и тем же зависимостям при различных значениях входящих в них переменных и производить многократный проход по одним и тем же участкам алгоритма. Такие участки называются циклами. Алгоритмы, содержащие циклы, называется циклическими. Использование циклов существенно сокращает объем алгоритма.
Различают циклы с наперед известным и наперед неизвестным количеством проходов.
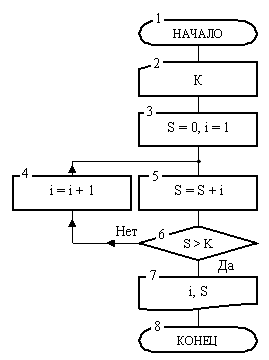
Блок-схема алгоритма решения этой задачи приведена на рис. 5. Она состоит из восьми блоков.
После начала работы в блоке 2 вводится значение числа К. Далее в блоке 3 переменная i получает значение 1, т. е. значение, с которого начнется отсчет натуральных чисел. Переменная S, предназначенная для накопления сумма этих чисел, перед началом суммирования получает значение 0. После этого управление передается блоку 5.
Нужно обратить внимание на то, что если бы до этой операции в блоке 3 не была выполнена команда S = 0 (записать нуль в ячейку S ), то при нахождении суммы S + 1 возникла бы ошибка, поскольку из ячейки S была бы извлечена константа, которая оказалась там после распределения памяти.
После суммирования первого члена последовательности в блоке 6 выполняется проверка условия о превышении суммы S заданного числа К.
Если условие 6 не выполнится, то производится переход к блоку 4, где при выполнении операции значение переменной увеличивается на 1 и становится равным 2. Теперь алгоритм вновь вернется к блоку 5 и к старому значении суммы добавит новый член 2. После этого сумма станет равной 3. В блоке б вновь проверяется условие получения требуемой суммы и т. д. Цепочка блоков 5-4 будет обрабатываться вновь и вновь до того момента, когда однажды при определенном значении переменной i, наконец, выполнится условие S > К, т. е. когда накапливаемая в таком цикле сумма впервые превысит заданное значение К. Переменная i, значение которой при очередном проходе цепочки этих блоков увеличивается на 1, играет роль счетчика этого цикла.
Рис. 5. Циклический алгоритм
Другие способы изображения циклов
Рис. 6. Структура цикла,
использующего символ «Цикл»
Рис. 7. Структура цикла, использующая
символ «Подготовка»
На рис. 6. показана структура цикла, которая может быть использована, когда условие выхода из цикла определяется символом его начала или символом его конца. Наряду с этим в качестве заголовка цикла может быть использован и символ «Подготовка». Структура такого цикла показана на рис. 7.
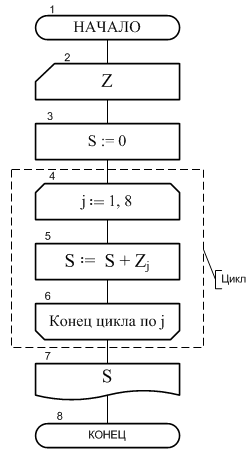
Пример 2. Теперь приведем пример алгоритма, содержащего цикл с наперед известным количеством проходов (повторений). Алгоритм решает задачу накопления суммы положительных элементов одномерного массива Z длины N (под длиной массива понимается количество его элементов).
Следует подчеркнуть, что если бы ввод этих переменных в блоке 2 производился в противоположном порядке, то это привело бы к ошибке. Действительно, невозможно заполнить N ячеек массива Z, когда значение переменной N еще не известно.
Далее в блоке 3 переменной S присвоено начальное значение 0. Это сделано для того, чтобы приготовить ячейку к накоплению необходимой суммы.
Рис. 8. Циклический алгоритм
Тест на алгоритм Министерства образования и науки РФ
Таким образом, выделенный блок выполнится при x = 2; y = 4; z = 1 (вариант 2 ).
Нередко при алгоритмическом решении задачи возникает необходимость создания цикла, содержащего в своем теле другой цикл. Такие вложенные друг в друга циклы относятся к структурам вложенных циклов. Порядок вложенности циклов, когда в теле внутреннего цикла содержатся другие циклы, может быть достаточно большим. Этот порядок определяется методом, с помощью которого достигается решение поставленной задачи. Так, при обработке одномерных массивов, как правило, удается построить алгоритмическую схему без вложения циклов. Однако в ряде случаев при решении таких задач без вложенных циклов не обойтись.
Отметим, что все вложенные друг в друга циклы, включая наружный, должны иметь счетчики с различными именами. Вне этих циклов счетчики могут быть использованы как обычные переменные или как счетчики других циклов.
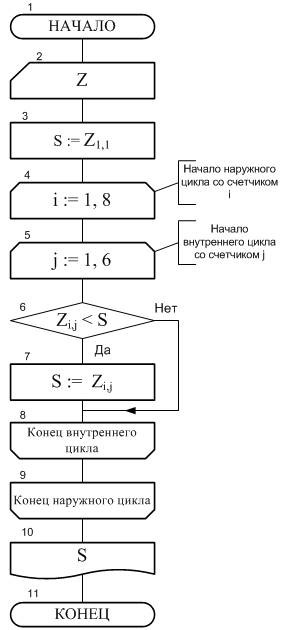
Пример 1. Рассмотрим задачу нахождения наименьшего элемента в двумерном массиве Z размером 8 х 6 .
После завершения работы внутреннего цикла произойдет возврат к заголовку наружного цикла, где значение переменной i увеличится на 1 и станет равным i = 2. Затем вновь выполнится весь внутренний цикл, что соответствует проходу по всем элементам второй строки массива Z.
Таким образом, после завершения наружного цикла будет совершен проход по всем элементам массива и в переменной S будет находиться константа, равная значению наименьшего элемента массива Z.
В блоке 10 будет выведено это значение и затем в блоке 11 алгоритм закончит свою работу.
Рис. 9. Алгоритм нахождения наименьшего элемента в двумерном массиве
Вспомогательный алгоритм является аналогом компьютерной подпрограммы. Он имеет имя и может иметь параметры, которые называются формальными параметрами. Имя служит для того чтобы отличить такой алгоритм от других алгоритмов, а формальные параметры, которые напоминают переменные математических функций, выполняют роль входных и выходных параметров.
Формальные параметры должны быть выбраны таким образом, чтобы ими был исчерпан весь набор необходимых входных и выходных величин. Нередко один и тот же параметр может оказаться входным и выходным одновременно. Например, на вход такого алгоритма может быть подан массив для обработки, а на выходе процедуры он может предстать в измененном виде как выходной параметр.
С помощью этого имени в алгоритме рис. 11 выполняется обращение к этой процедуре. Параметры, которые при вызове алгоритма подставляют на место формальных, называются фактическими параметрами.
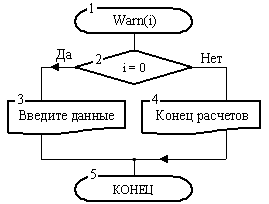
Из схемы рис. 11 видно, что если при обращении к процедуре Warn на ее вход подать i = 0, то она в блоке 3 выдаст сообщение «Введите данные». При любом другом i будет выведено сообщение «Конец расчетов». Этим исчерпываются возможности процедура Warn.
Рис. 10. Процедура Warn
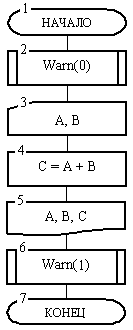
На рис. 11 дана схема головного алгоритма (первый блок имеет наименование «Начало»). Этот алгоритм в блоках 2 и 8 обращается к процедуре Warn (вызывает ее). Опишем последовательность и механизм обработки данных, которые предписаны алгоритмами рис. 10 и 11.
Выполнение алгоритмических действий всегда начинаются с головного алгоритма. Поэтому сначала будет выполнен блок 1 схемы рис. 11. Далее в блоке 2 головной алгоритм выполняет обращение к процедуре Warn при конкретном значении ее аргумента (0).
Далее в блоках 3-5 алгоритма рис. 11 выполняются уже понятные действия по вводу, суммированию и выводу переменных. Затем управление передается в блок б, который содержит новое обращение к процедуре Warn с фактическим параметром 1.
Снова управление переключается на схему рис. 10, где вместо формального параметра i всюду записывается фактический параметр – константа 1. Поскольку в блоке 2 условие 1 = 0 не выполнится, то будет выполнен блок 4 и алгоритм выведет сообщение «Конец расчетов».
После этого управление возвращается в головной алгоритм к блоку 7, где и будет окончательно завершен алгоритмический процесс.
Рис. 11. Головной алгоритм
Внешне такой процесс может выглядеть примерно так.
На экран выводится сообщение «Введите данные» и компьютер переходит в режим ожидания ввода двух констант с клавиатуры. Затем после их ввода на экране появляется три константы и надпись «Конец работы».
На первый взгляд может показаться, что процедуры лишь усложняют решение задачи.
Действительно, рассмотренную здесь задачу проще решить одним алгоритмом, не прибегая к составление процедуры. Однако при составлении алгоритма решения сложной задачи очень быстро становится ясно, что без использования процедур обойтись просто невозможно. На практике при решением серьезных алгоритмических задач часто одному программисту не под силу выполнить весь объем работ. Поэтому над ее решением работает обычно коллектив программистов под руководством координатора. Образно говоря, координатор здесь работает как головной алгоритм, а его программисты как процедуры. При этом каждый программист (часто независимо от других) получает от координатора задание по составление процедур определенного назначения. В результате такой организации работы задача получает разрешение.
Под декомпозицией алгоритма понимают разложение его o 6щeй алгоритмической схемы на вспомогательные алгоритмы (процедуры и функции) и головной алгоритм. Напомним, такая задача ставится перед студентом при выполнении курсовой или контрольной работы. Одним из условий, которое должно быть обязательно выполнено, является наличие в работе хотя бы одной процедуры или функции (кроме того, работа должна содержать текст описания всех вспомогательных алгоритмов и головного алгоритма).
Метод, при помощи которого обычно выполняется декомпозиция, достаточно прост. Сначала вычленяют основные этапы предстоящей работы. Наиболее сложные этапы оформляют в виде вспомогательных алгоритмов верхнего уровня. Затем, если необходимо, такие этапы делят на этапы более низкого уровня. Наиболее сложные из них также оформляют вспомогательными алгоритмами и т. д. Следуя методу «от сложного к простому», в конечном итоге получают решение поставленной задачи.
Приведем пример декомпозиции для решения задачи сортировки массива в порядке возрастания его элементов.
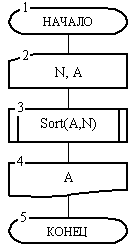
Решение задачи декомпозиции состоит из трех основных этапов: 1) ввода данных, 2) сортировки массива и 3) вывода отсортированного массива. Первый и третий этапы вследствие их простоты не нуждаются в декомпозиции, поэтому выполняются в головном алгоритме. Второй этап представляет достаточно сложный и самостоятельный фрагмент алгоритмической работы, поэтому его целесообразно выделить в отдельную процедуру, которой можно дать имя Sort.
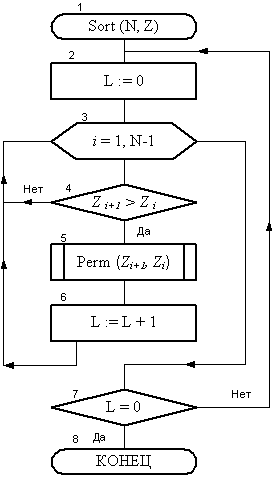
Выполним далее сортировку массива в порядке возрастания его элементов «методом пузырька». Этот метод достаточно прост. Сначала совершают проход по всем соседним парам элементов массива и в случае, если они не отсортированы, то значения элементов всякой такой пары меняют местами. Если была совершена хотя бы одна перестановка, то такую процедуру повторяют до тех пор, пока при проходе по массиву не будет совершено ни одной перестановки. В результате массив будет отсортирован.
После сортировки в блоке 4 головного алгоритма отсортированный массив будет выведен и в блоке 5 алгоритм закончит свою работу.
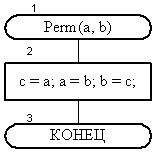
Рис. 12. Процедура Perm
Рис. 13. Процедура Sort
Рис. 14. Головной алгоритм
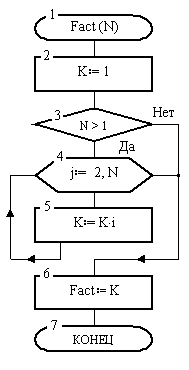
В заключение приведем пример алгоритма-функции. Она похожа на вспомогательный алгоритм-процедуру, но в отличие от последней должна в своем теле содержать команду присваивания результата имени функции, т. к. результат после вычислений сохранится в переменной, представленной именем функции.
Обращение к функции в других алгоритмах (головных, процедурах, функциях) производится по ее имени.
При этом оно может входить в состав выражений. В качестве фактических параметров могут быть использованы как переменные, константы, так и целые выражения. Важно только, чтобы фактический параметр был совместим по типу с формальным, который содержится в заголовке описания алгоритма.
Рис. 15. Функция Fact
Рис. 16. Обращение к функции Fact
Тест на вспомогательный алгоритм
Если обратиться к алгоритму
при помощи оператора