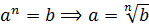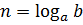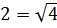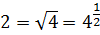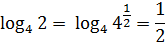логарифм зачем нужен в жизни
Что такое логарифм? Зачем нужны логарифмы?
Логарифмы — традиционная головная боль для многих учеников старших классов. Особенно — уравнения и неравенства с логарифмами. Не любят старшеклассники логарифмы почему-то. И поэтому боятся. И совершенно зря.) Ибо сам по себе логарифм — это очень и очень простое понятие. Не верите? Убедитесь сами! В сегодняшнем уроке.
Итак, поехали знакомиться.)
Для начала решим в уме вот такое очень простенькое уравнение:
Это простейшее показательное уравнение. Оно так называется из-за того, что неизвестное икс находится в показателе степени. Даже если вы не в курсе, как решаются показательные уравнения, просто в уме подберите икс так, чтобы равенство выполнилось. Ну же?! Ну, конечно же, х = 2. Два в квадрате — это четыре.)
А теперь я изменю в нём всего одно число. Вот такое уравнение теперь решим:
И снова пробуем подобрать икс…
Что, никак не подбирается? Два в квадрате — это четыре. Два в кубе — это уже восемь. А у нас — пятёрка. Мимо проскочили… Что делать? Только не говорите мне, что нету такого икса! Не поверю.)
Согласитесь, что это как-то несправедливо: с четвёркой уравнение решается в уме, а с пятёркой — уже не решается никак. Математика не приемлет такой дискриминации! Для неё все числа — равноправные партнёры.)
На данном этапе мы можем лишь грубо прикинуть, что икс — какое-то дробное число между двойкой (2 2 = 4) и тройкой (2 3 = 8). Можем даже немного повозиться с калькулятором и приближённо подобрать, найти это число. Но такая возня каждый раз… Согласен, как-то грустно…
Математика решает данную проблему очень просто и элегантно — введением понятия логарифма.
Итак, что же такое логарифм? Вернёмся к нашему загадочному уравнению:
Осмысливаем задачу: нам надо найти некое число х, в которое надо возвести 2, чтобы получить 5. Понятна эта фраза? Если нет, перечитайте ещё раз. И ещё… Пока не осознаете. Ибо это очень важно!
Вот и назовём это загадочное число х логарифмом пятёрки по основанию два! В математической форме эти слова выглядят так:
А произносится эта запись вот так: «Икс равен логарифму пяти по основанию два.»
Ну, вот, собственно, и всё! Мы решили ужасное на вид показательное уравнение!
И всё! Это правильный и совершенно полноценный ответ!
Может быть, вас смущает, что вместо конкретного числа я пишу какие-то непонятные буковки и значки?
Ну что ж, ладно, уговорили… Специально для вас:
x = log25 = 2,321928095…
Имейте в виду, что число это никогда не кончается. Да-да! Иррациональное оно…
Вот вам и ответ на вопрос, для чего нужны логарифмы. Логарифмы нам нужны, в первую очередь, для решения показательных уравнений! Таких, которые без логарифмов и не решаются вовсе…
Например, решая показательное уравнение
про логарифмы можно не вспоминать. Сразу ясно, что х = 2.
А вот, решая уравнение, скажем, такое
вы приближённо получите вот такой лохматый ответ:
Зато через логарифм даётся абсолютно точный ответ:
И все дела.) Вот поэтому и пишут логарифмы вместо некрасивых иррациональных чисел. Кому нужен числовой ответ — посчитает на калькуляторе или хотя бы в Excel.) А раньше, когда калькуляторов и компьютеров не было и в помине, существовали специальные таблицы логарифмов. Объёмные и увесистые. Так же, как и таблицы Брадиса для синусов и косинусов. И даже инструмент такой был — логарифмическая линейка. Которая позволяла с хорошей точностью вычислять массу полезных вещей. И не только логарифмы.)
Ну вот. Теперь, незаметно для себя, мы научились решать все показательные уравнения такого зверского типа.
Это всё верные ответы! Ну как? Заманчиво, правда?
А теперь вдумаемся в смысл самой операции нахождения логарифма.
Как мы знаем, на каждое действие математики стараются найти противодействие (т.е. обратное действие). Для сложения это вычитание, для умножения это деление. А какое обратное действие есть для возведения в степень?
Давайте посмотрим. Какие у нас основные действующие фигуры при возведении в степень? Вот они:
b — собственно сама степень.
А теперь подумаем: если нам известна степень (b) и известен показатель этой самой степени (n), а найти надо основание (a), то что мы обычно делаем? Правильно! Извлекаем корень n-й степени! Вот так:
А теперь посмотрим на другую ситуацию: нам снова известна степень (b), но на этот раз вместо показателя n нам известно основание (a), а найти как раз надо этот самый показатель (n). Что делать будем?
Вот тут-то на помощь и приходят логарифмы! Прямо так и пишут:
«Эн» (n) — это число, в которое надо возвести «a», чтобы получить «b». Вот и всё. Вот и весь смысл логарифма. Операция нахождения логарифма — это всего лишь поиск показателя степени по известным степени и основанию.
Простейшие примеры с логарифмами.
А теперь новость не очень хорошая. Если логарифм считается ровно, то его надо считать, да.
Скажем, если где-то в уравнении вы получили
то такой ответ никто не оценит. Надо логарифм посчитать и записать:
А как мы поняли, что log39=2? Переводим равенство с математического языка на русский: логарифм девяти по основанию три — это число, в которое надо возвести три, чтобы получить девять. И в какое же число надо возвести тройку, чтобы получить девятку? Ну, конечно! В квадрат надо возвести. То есть, в двойку.)
А чему равен, скажем, log5125? А в какой степени пятёрка даёт нам 125? В третьей, разумеется (т.е. в кубе)!
Стало быть, log5125 = 3.
В какую степень надо возвести 7, чтобы получить 7? В первую!
Вот вам и ответ: log77 = 1
А вот такой пример как вам?
И в какую же степень надо возвести тройку, чтобы получить единицу? Неужели не догадались? А вы вспомните свойства степеней .) Да! В нулевую! Вот и пишем:
Уловили принцип? Тогда тренируемся:
Ответы (в беспорядке): 1; 3; 5; 0; 4.
Что? Забыли, в какой степени 3 даёт 243? Что ж, ничего не поделаешь: степени популярных чисел надо узнавать. В лицо! Ну, и таблица умножения — надёжный спутник и помощник. И не только в логарифмах.)
Ну вот, совсем простенькие примеры порешали, а теперь шагаем на ступеньку выше. Вспоминаем отрицательные и дробные показатели.)
Решаем вот такой пример:
Мда… И в какую же степень надо возвести четвёрку, чтобы получить 0,25? Так с ходу и не скажешь. Если работать только с натуральными показателями. Но степени в математике, как известно, бывают не только натуральными. Самое время подключить наши знания об отрицательных показателях и вспомнить, что
Стало быть, можно смело записать:
В какую такую степень надо возвести четвёрку, чтобы получить двойку? Для ответа на этот вопрос придётся подключать наши знания о корнях. И вспомнить, что двойка — это корень квадратный из четырёх:
А корень квадратный математика позволяет представить в виде степени! С показателем 1/2. Так и пишем:
Поэтому наш логарифм будет равен:
Ну что, поздравляю! Вот мы с вами и познакомились с логарифмами. На самом примитивном начальном уровне.) И вы сами лично убедились, что они вовсе не так страшны, как, возможно, вам казалось раньше. Но у логарифмов, как и у любых других математических понятий, есть свои свойства и свои особые фишки. О том и о другом (о свойствах и о фишках) — в следующем уроке.
Для чего нужны логарифмы?
Слово «логарифм» многие бывшие ученики общеобразовательных учреждений помнят со школьных уроков математики. Эта тема некоторым из них казалась сложной и непонятной. Не все из них действительно поняли, что такое логарифмы и для чего они нужны. Попробуем разобраться в этом вместе с вами.
Конечно, в математике есть определение этого слова, но оно не всем может показаться понятным. Логарифмирование – это действие, которое обратно возведению в степень. Неподготовленному человеку трудно понять, что означают эти слова, и какая от всего этого польза.
Что же это такое и как с этим можно работать?
Допустим, нужно найти х в уравнении 5 х = 12. В этом случае х будет равен числу, в которое надо возвести 5, чтобы получилось 12. Используя логарифм, этот пример будет звучать так: х равен логарифму 12 по основанию 5. А выгладит уравнение так: х = log512. Если произвести вычисление на калькуляторе или компьютере, то получается иррациональное число. Чтобы было легче работать с такими числами, и создали такую математическую конструкцию, как логарифм.
Говоря простым языком, они нужны для упрощения трудных вычислений. Логарифмы обладают важными свойствами, благодаря которым умножение можно заменить простым сложением, а извлечение корня и его возведение в степень можно преобразовать в умножение и в деление.
Применение свойств логарифмов в жизнедеятельности человека
Если логарифмы имеют одинаковое основание, то их сумма равна логарифму произведения, а разность – частного. И получается, что при математических действиях со сложными иррациональными числами, результатом становятся привычные всем натуральные числа. Если основания логарифма разные, то их можно преобразовать по формулам перехода к новому основанию.
Для упрощения подобных вычислений были созданы логарифмические таблицы. С их помощью можно было легко умножать числа, складывая их логарифмы. Более 300 лет такие таблицы расширялись и уточнялись многими математиками. С появлением возможности электронных вычислений, пользоваться логарифмами стало ещё проще. Таблицы теперь используют только в узкоспециализированных сферах.
Свойства логарифмов на практике пригодятся многим людям, занятым на производстве и в научных сферах, в которых необходимы трудоёмкие вычисления. С их помощью можно сравнивать величины, значительно отличающиеся друг от друга. Если вы нарисуете обычный график, на котором отмечены значения 10, 100 и 100 000, то маленькие значения будут практически около ноля. Но логарифмическая линейка позволяет сделать изображение таких чисел более наглядным. С помощью подобных схем часто проводится анализ сравнения шумов, что бывает полезным во многих сферах.
Где можно получить больше информации о свойствах логарифмов?
Пропустили занятие в школе, готовитесь к ЕГЭ или просто интересуетесь математикой? Тогда вам может пригодиться видеоурок на тему «Свойства логарифмов. Логарифм степени», который можно найти, перейдя по ссылке http://interneturok.ru/algebra/11-klass/pokazatelnaya-i-logarifmicheskaya-funktsii/svoystva-logarifmov-logarifm-stepeni.
В рамках занятия преподаватель не только расскажет о формуле логарифма степени, но и докажет её и напомнит некоторые важные свойства логарифмов. Также можно узнать, как использовать свойства логарифма при решении распространенных примеров. Видеоурок дополнен иллюстрированным текстовым конспектом, в котором также можно найти необходимую информацию.
Логарифм зачем нужен в жизни
Изучение темы «Логарифмы» начинается с определения:
Логарифмом положительного числа b по основанию a, где a > 0, a ≠ 1, называется показатель степени, в которую надо возвести число a, чтобы получить число b.
Обычно, такая первая встреча с логарифмами не вызывает у учеников особой радости и энтузиазма, логарифм невольно ассоциируется с чем-то трудным. Многие ворчат: «Ну, кому понадобились эти логарифмы?».
Я тоже задумался над этим и решил узнать мнения людей, окончивших школу, по этому вопросу. Результаты меня озадачили: из 20 опрошенных 15 (75%) считают, что логарифмы не нужно изучать. Так может быть они действительно не нужны? Меня очень заинтересовала эта проблема.
Предмет исследования – частные вопросы создания и применения логарифмов.
Проблема: логарифмы – прихоть математиков или жизненная необходимость?
Гипотеза: логарифмы нужны современному человеку.
Существует связь между звездами, шумом, музыкой, природой и логарифмами.
Цель работы – доказать необходимость изучения логарифмов.
Для достижения своей цели, я выдвинул следующие задачи:
найти, собрать и проанализировать материал по истории возникновения логарифмов;
проанализировать, где в природе встречаются логарифмы;
проанализировать, в каких сферах жизнедеятельности человека применяются логарифмы;
сделать соответствующие выводы по исследовательской работе.
При проведении исследования были использованы следующие методы исследования:
анализ существующей литературы по рассматриваемой проблеме (метод научного анализа).
обобщение и синтез точек зрения, представленных в литературе (метод научного синтеза и обобщения).
моделирование на основе полученных данных авторского видения в раскрытии поставленной проблемы (метод моделирования).
2.1. История возникновения и развития логарифмов
Изобретение логарифмов, сократив
работу астронома, продлило ему жизнь.
Испокон веков люди пытались упростить вычисления: составляли таблицы, вводили приближенные формулы, облегчающие расчеты, пытались заменить сложные операции умножения и деления более простыми – сложением и вычитанием.
Логарифмы также были созданы в 16 веке как средство для упрощения вычислений. В их основе лежит очень простая идея, знакомство с которой приписывается еще Архимеду.
Рассмотрим две прогрессии, арифметическую и геометрическую при b1 = 2, q = 2
1 2 3 4 5 6 7 8 9 10 (*)
2 4 8 16 32 64 128 256 512 1024
Но это еще не все. С помощью указанных двух строк (*) действие возведения в степень заменяется умножением, а извлечение корня – делением.
Идея Архимеда получила развитие не сразу. Пока математикам было достаточно уже имевшихся средств вычислений, они проходили мимо этого удивительного свойства прогрессий. Но в эпоху Возрождения ситуация изменилась. Крупнейшие европейские державы стремились к владычеству на море. Для дальних плаваний, для определения положения морских судов по звездам и по солнцу необходимо было всё более развивать астрономию, а значит, и тригонометрию. И, в частности, понадобились более совершенные тригонометрические таблицы. В связи с нарастающими запросами практики продолжали совершенствоваться астрономические инструменты, увеличивалась точность наблюдений, исследовались планетные движения. Обработка полученных данных требовала колоссальных расчетов, и, следовательно, стали необходимы новые средства упрощения вычислений. Такими средствами в 15 – 16 веках явились в первую очередь логарифмы и десятичные дроби.
Рассмотрим, как развивалась дальше идея логарифмов.
Прежде всего, теоретическая подготовка учения о логарифмах тесно связана с развитием понятия степени. Степень с отрицательным показателем встречается уже в трактате «Арифметика» древнегреческого математика Диофанта (ок. 3 в.) из Александрии. Им, а возможно и его предшественниками, были введены особые обозначения для некоторых положительных и отрицательных степеней. С течением времени символика совершенствовалась, и эта идея получила дальнейшее развитие. Так, много позже, французский врач и математик Никола Шюке (ок. 1445 – 1500) в своем трактате «Наука о числе» более полно рассмотрел нулевые и отрицательные показатели степени. Ещё раньше, в 14 веке, епископ города Лизье в Нормандии Николай Орем (ок. 1323 – 1382), исходя из соображений о возможности вставлять в арифметическом ряду между натуральными числами дробные, высказал мысль о том, как надо выражать в рядах (*) соответствующие величины геометрического ряда. Таким образом, он пришел к степеням с дробным показателем.
Особое внимание сопоставлению арифметического и геометрического рядов уделял Михаэль Штифель (1487 – 1567). Подобно Шюке и Орему Штифель пришел к мысли о дробных показателях. Кроме того, сопоставляя ряд натуральных чисел, начинающихся единицей, он отмечал, что соответствующий единице показатель есть нуль, т.е. что a 0 = 1. Числам верхнего ряда Штифель дал употребительное и поныне название «показателей» (exponent).
Но, кто же стал автором первых таблиц логарифмов, позволяющих свести более сложные действия к более простым?
В истории науки иногда наступают моменты, когда необходимость некоторого открытия осознается многими, а его основная идея как бы витает в воздухе. В таких случаях к открытию приходят не один, а сразу несколько ученых. Так случилось и в истории логарифмов. Однако создатели первых логарифмических таблиц подходили к изобретению нового удобного средства для упрощения вычислений по-разному. Те соображения, которые мы выдвинули чуть раньше, пытаясь предугадать, каким путем пойдет создатель логарифмов, пожалуй, больше всего подходят к Бюрги.
Таблицы Иоста Бюрги были ещё очень несовершенны, правила работы с ними достаточно трудоемки, а многие результаты приходилось находить с помощью дополнительных приближенных приемов вычислений.
Бюрги очень медлил с опубликованием своих таблиц. Они вышли в свет лишь в 1620 году под названием «Таблицы арифметической и геометрической прогрессий, вместе с основательным наставлением, как их нужно понимать и с пользой применять во всяческих вычислениях». Но значительного распространения эти таблицы не получили, так как к моменту опубликования таблиц Бюрги ученому миру уже семь лет были известны другие таблицы, которые составил шотландский барон Джон Непер (1550 – 1617).
Интересно, что наряду с вышеуказанными таблицами существовали ещё одни таблицы, которыми можно было пользоваться как средством для упрощения вычислений. Однако их автор не заметил этого, подразумевая совсем иное назначение своих таблиц. Речь идет о таблицах процентов шотландского ученого и инженера Симона Стевина (1548 – 1620).
Итак, можно заметить, что в один смысловой блок собираются такие понятия, как арифметическая и геометрическая прогрессии, степень, проценты, формула сложных процентов и логарифмы.
2.2. Применение логарифмов для познания окружающего мира
Если в 16 веке логарифмы появились как средство для упрощения вычислений, то нужны ли они сегодня, когда вычислительная техника достаточно развита, чтобы справляться с самыми сложными расчетами? Вопрос правомерен. Ведь не изучают же в современной школе такие старые средства для упрощения вычислений, как простейшие счетные приборы, не изучаются древние алгоритмы умножения и деления чисел, извлечения квадратных и кубических корней и прочее. Так зачем изучают логарифмы сегодня? Попробуем ответить на этот интересный вопрос.
Во-первых, логарифмы и сегодня позволяют упрощать вычисления.
Во-вторых, испокон веков целью математической науки было помочь людям узнать больше об окружающем мире, познать его закономерности и тайны.
Ряд явлений природы помогает описать логарифмическая зависимость. Иначе говоря, математики, пытаясь составить математическую модель того или иного явления, достаточно часто обращаются именно к логарифмической функции.
Одним из наиболее наглядных примеров такого обращения является логарифмическая спираль. (см. Приложение 1.) Спираль в одну сторону развертывается до бесконечности, а вокруг полюса, напротив, закручивается, стремясь к нему, но не достигая.
a ) Логарифмическая спираль в природе.
Так почему в качестве примера логарифмической зависимости в природе выбирают именно логарифмическую спираль?
Немецкий биолог Румблер в 1910 году выдвинул теорию постоянного краевого угла при построении раковин улиток. Он исходил из того, что материал, из которого строятся раковины, вначале должен быть жидким, и в жидком состоянии попадает на край уже существующей части раковины где, естественно, всегда образуется постоянный краевой угол. Под этим углом жидкость затвердевает, и снова начинается та же игра. Раковина улитки представляет собой логарифмическую спираль.
Но не только раковины многих моллюсков, улиток, а даже рога таких млекопитающих, как архары (горные козлы), закручены по логарифмической спирали (см. Приложение 3.)
Можно сказать, что эта спираль является математическим символом соотношения формы и роста. Великий немецкий поэт Иоганн-Вольфганг Гёте считал её даже математическим символом жизни и духовного развития.
По логарифмической спирали очерчены не только раковины, но и в подсолнухе семечки (см. Приложение 4) расположены по дугам, близким к логарифмической спирали и т. д. Один из наиболее распространённых пауков – эпейра, сплетает нити паутины вокруг центра по логарифмическим спиралям (см. Приложение 5).
b ) Звёзды, шум и логарифмы.
Известно, что астрономы распределяют звезды по степеням видимой яркости на светила первой величины, второй величины, третьей и т.д. Последовательные звездные величины воспринимаются глазом как члены арифметической прогрессии. Но физическая яркость их изменяется по иному закону: объективные яркости составляют геометрическую прогрессию со знаменателем 2,5. Получается, что «величина» звезды представляет собой не что иное, как логарифм её физической яркости. Оценивая видимую яркость звёзд, астроном оперирует с таблицей логарифмов по основанию 2,5.
Рассмотрим несколько примеров. Тихий шелест листьев оценивается в 1 бел, громкая разговорная речь – в 6,5 бел, рычание льва – в 8,7 бела. Отсюда следует, что по силе звука разговорная речь превышает шелест листьев в раз; львиное рычание сильнее громкой разговорной речи в раз.
Случайность ли то, что и при оценке видимой яркости светил и при измерении громкости шума мы имеем дело с логарифмической зависимостью между величиной ощущения и порождающего его раздражения? Нет, и то, и другое – следствие общего закона (называемого «психофизическим законом Фехнера»), гласящего: величина ощущения пропорциональна логарифму величины раздражения. Как видим, логарифмы вторгаются и в область психологии.
c ) Логарифмическая спираль в технике.
Логарифмическая спираль знаменита не только тем, что её образы достаточно широко встречаются в природе, но и своими удивительными свойствами.
В технике часто применяют вращающиеся ножи. Сила, с которой они давят на разрезаемый материал, зависит от угла резания, т.е. угла между лезвием ножа и направлением скорости вращения. Для постоянства давления нужно, чтобы угол резания сохранял постоянное значение, а это будет в том случае, если лезвия ножей очерчены по дуге логарифмической спирали (см. Приложение 7).Величина угла резания зависит от обрабатываемого материала.
В гидротехнике по логарифмической спирали изгибают трубу, подводящую поток воды к лопастям турбины (см. Приложение 7). Благодаря такой форме трубы потери энергии на изменение и направление течения в трубе оказываются минимальными и напор воды используется с максимальной производительностью.
Пропорциональность длины дуги спирали радиус-вектору используют при проектировании зубчатых колёс с переменным передаточным числом. И через середину и конец каждой стороны проводят дуги одинаковых логарифмических спиралей (см. Приложение 7) с полюсами в центрах квадратов, причем одна спираль закручивается по часовой стрелке, а другая – против часовой стрелки. Тогда при вращении этих квадратов дуги спиралей будут катиться одна по другой без скольжения. Передаточное же число, т.е. отношение угловых скоростей этих колёс, будет непрерывно меняться, достигая в течение одного оборота колеса четыре раза максимального значения и четыре раза минимального.
d) Логарифмы и музыка.
«Даже изящные искусства питаются ею.
Разве музыкальная гамма не есть
Набор передовых логарифмов?»
И действительно, так называемые ступени темперированной хроматической гаммы (12-звуковой) частот звуковых колебаний представляют собой логарифмы. Только основание этих логарифмов равно 2 (а не 10, как принято в других случаях).
Логарифмируя эту формулу, получаем
lg = lg n + m lg 2 + + p ( lg 2)/12,
lg = lg n + (m + p/12)lg2.
Принимая частоту самого низкого “до” за единицу (n = 1) и приводя все логарифмы к основанию 2. имеем
e ) Логарифмы в разных отраслях науки
Логарифмы – это математическое понятие, которое применяется во всех отраслях науки: химии, биологии, физике, механике, информатике, электротехнике, географии и многих других.
Статистика постоянно использует понятие среднего. Средняя численность населения, средний уровень инфляции, средняя заработная плата и т.д. Для нахождения средних величин существует коэффициент усреднения он равен ln=2.
Сведения, собранные мною в данной работе, — это далеко не всё, что можно рассказать о логарифмах. В заключении обратимся еще раз к основной идее. Мы, обучаясь в школе, не просто впитываем некоторый набор информации. Мы усваиваем научные данные об окружающем мире, о его устройстве и законах. В этот период складывается картина мира, и чем полнее и объективнее она будет, тем лучше мы будем понимать и оценивать окружающую нас жизнь, тем более полноценными людьми будем себя ощущать. Поэтому стоит изучать вопросы, без которых картина мира будет неполноценной. С моей точки зрения, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы счисления.
Результаты моего исследования следующие:
В ходе проведения исследовательской работы я нашел подтверждение словам Галилео Галилея «Великая книга природы написана математическими символами»;
Многие природные явления не могли быть изучены без понятия логарифма;
Логарифмы используются для описания природных явлений астрономами, физиками, биологами;
Понятие логарифма широко применяется человеком во многих науках.
Логарифм является инструментом для вычисления радиоактивного распада, изменения количества людей в стране, зависимости скорости ракеты от ее массы, коэффициента звукоизоляции.
Выяснил, что, играя по клавишам современного рояля, музыкант играет, собственно говоря, на логарифмах.
Материалы исследования имеют практическую значимость и могут быть использованы для дальнейшего изучения данной, столь увлекательной, на мой взгляд, темы.
Гипотеза моего исследования, что логарифмы нужны современному человеку, действительно подтвердилась.
Я постарался проследить, как в ходе истории возникала необходимость введения и изучения логарифмов, усиливалась их значимость. Показал применение логарифмов в современном мире. Тем самым, я смог доказать, насколько важно изучать логарифмы для познания окружающего мира.
Алимов Ш.А. Алгебра и начала анализа.- М.:Просвещение,2016.
Большая электронная энциклопедия «Кирилл и Мефодий»: 2004
Виленкин Н.Я. Алгебра и математический анализ.- М.:Мнемозина,2017.
Колмогоров А.Н. Алгебра и начала анализа.- М.:Просвещение,2016.
Лиман М.М. Школьникам о математике и математиках.- М.:Просвещение,1981.
Самсонов П.И. «Математика»:«Полный курс логарифмов. Естественнонаучный профиль». «Школьная пресса», М.2005
Энциклопедия для детей. Т. 11. Математика. – М.: Аванта+, 1998.
Приложение 1. Логарифмическая спираль.
Приложение 2. Раковины многих моллюсков, улиток закручены по логарифмической спирали.
Приложение 3. Рога таких млекопитающих, как архары (горные козлы), закручены по логарифмической спирали.
Приложение 4. В подсолнухе семечки расположены по дугам, близким к логарифмической спирали.
Приложение 5. Паук – эпейр сплетает нити паутины вокруг центра по логарифмическим спиралям.
Приложение 6. По логарифмическим спиралям также закручены и многие галактики, в частности Галактика, которой принадлежит Солнечная система.
Приложение 7. Лезвия вращающихся ножей очерчены по дуге логарифмической спирали. В гидротехнике по логарифмической спирали изгибают трубу, подводящую поток воды к лопастям турбины.
Старт в науке
Учредителями Конкурса являются Международная ассоциация учёных, преподавателей и специалистов – Российская Академия Естествознания, редакция научного журнала «Международный школьный научный вестник», редакция журнала «Старт в науке».