метод монте карло почему так называется
Интуитивное использование методов Монте-Карло с цепями Маркова.
Легко ли это? Я попробовал.
Алексей Кузьмин, директор разработки и работы с данными ДомКлик, преподаватель факультета « Аналитика и Data Science » в Нетологии, перевёл статью Rahul Agarwal о том, как работают методы Монте-Карло с цепями Маркова для решения проблем с большим пространством состояний.
Каждый, кто связан с Data Science, хоть раз слышал о методах Монте-Карло с цепями Маркова (MCMC). Иногда тема затрагивается во время изучения байесовской статистики, иногда — при работе с такими инструментами, как Prophet.
Но MCMC трудно понять. Всякий раз, читая об этих методах, я замечал, что суть MCMC скрыта в глубоких слоях математического шума, и за этим шумом её тяжело разобрать. Мне пришлось потратить много часов, чтобы разобраться в этой концепции.
В этой статье — попытка объяснить методы Монте-Карло с цепями Маркова доступно, так, чтобы стало понятно, для чего они используются. Я остановлюсь ещё на нескольких способах использования этих методов в моём следующем посте.
Итак, начнём. MCMC состоит из двух терминов: Монте-Карло и Марковские цепи. Поговорим о каждом из них.
Монте-Карло
Методы Монте-Карло получили своё название от казино Монте-Карло в Монако. Во многих карточных играх нужно знать вероятность выиграть у дилера. Иногда вычисление этой вероятности может быть математически сложным или трудноразрешимым. Но мы всегда можем запустить компьютерную симуляцию, чтобы много раз воспроизвести всю игру и рассматривать вероятность как количество побед, разделённое на количество сыгранных игр.
Это всё, что вам нужно знать о методах Монте-Карло. Да, это просто несложная техника моделирования с причудливым названием.
Марковские цепи
Поскольку термин MCMC состоит из двух частей, нужно ещё понять, что такое цепи Маркова. Но прежде, чем перейти к Марковским цепям, немного поговорим о Марковских свойствах.
Предположим, есть система из M-возможных состояний и вы переходите из одного состояния в другое. Пусть пока вас ничего не сбивает с толку. Конкретный пример подобной системы — погода, которая меняется от жаркой к холодной и умеренной. Другой пример — фондовый рынок, который прыгает от «медвежьего» к «бычьему» и состоянию стагнации.
Марковское свойство говорит о том, что для данного процесса, который находится в состоянии Xn в конкретный момент времени, вероятность Xn + 1= k (где k — любое из M-состояний, в которое процесс может перейти) зависит только от того, каково это состояние в данный момент. А не о том, как оно достигло нынешнего состояния.
Говоря математическим языком, можем записать это в виде следующей формулы:
Для наглядности: вы не заботитесь о последовательности состояний, которые рынок принимал, чтобы стать «бычьим». Вероятность того, что следующее состояние будет «медвежьим», определяется только тем фактом, что рынок в настоящее время находится в «бычьем» состоянии. Это также имеет смысл на практике.
Процесс, обладающий Марковским свойством, называется Марковским процессом. Из-за чего же важна Марковская цепь? Из-за своего стационарного распределения.
Что такое стационарное распределение
Я попытаюсь объяснить стационарное распределение, рассчитав его для приведённого ниже примера. Предположим, у вас есть Марковский процесс для фондового рынка, как показано ниже.
У вас есть матрица переходных вероятностей, которая определяет вероятность перехода из состояния Xi в Xj.
В приведённой матрице переходных вероятностей Q вероятность того, что следующим состоянием будет «бык», учитывая текущее состояние «бык» = 0,9; вероятность того, что следующее состояние будет «медвежьим», если текущее состояние «бык» = 0,075. И так далее.
Что ж, давайте начнём с какого-то определённого состояния. Наше состояние будет задаваться вектором [бык, медведь, стагнация]. Если мы начнём с «медвежьего» состояния, вектор будет таким: [0,1,0]. Мы можем вычислить распределение вероятности для следующего состояния, умножив вектор текущего состояния на матрицу переходных вероятностей.
Заметьте, что вероятности дают в сумме 1.
Следующее распределение состояний можно найти по формуле:
И так далее. В конце концов, вы достигнете стационарного состояния, в котором состояние стабилизируется:
Вы можете получить стационарное распределение при помощи следующего кода:
Вы также можете начать с любого другого состояния — достигнете того же стационарного распределения. Измените начальное состояние в коде, если хотите в этом убедиться.
Теперь мы можем ответить на вопрос, почему же стационарное распределение так важно.
Стационарное распределение важно, потому что с его помощью можно определять вероятность системы быть в определенном состоянии в случайное время.
Для нашего примера можно сказать, что в 62,5% случаев рынок будет в «бычьем» состоянии, 31,25% — в «медвежьем» и 6,25% — в стагнации.
Интуитивно вы можете рассматривать это как случайное блуждание по цепи.
Вы находитесь в определенной точке и выбираете следующее состояние, наблюдая распределение вероятностей следующего состояния с учётом текущего состояния. Мы можем посещать некоторые узлы чаще, чем другие, основываясь на вероятностях этих узлов.
Именно таким образом на заре интернета Google решил проблему поиска. Проблема заключалась в сортировке страниц, в зависимости от их важности. В Google решили задачу, используя алгоритм Pagerank. В алгоритме Google Pagerank следует рассматривать состояние как страницу, а вероятность страницы в стационарном распределении — как ее относительную значимость.
Теперь перейдём непосредственно к рассмотрению методов MCMC.
Что такое методы Монте-Карло с цепями Маркова (MCMC)
Прежде чем ответить, что же такое MCMC, позвольте задать один вопрос. Мы знаем о бета-распределении. Мы знаем его функцию плотности вероятностей. Но можем ли мы взять выборку из этого распределения? Вы можете придумать способ, как это сделать?
MCMC даёт возможность выбрать из любого распределения вероятностей. Это особенно важно, когда нужно сделать выборку из апостериорного распределения.
Например, нужно сделать сэмпл из апостериорного распределения. Но легко ли вычислить апостериорную компоненту вместе с нормирующей постоянной (evidence)? В большинстве случаев можно найти их в виде произведения правдоподобия и априорной вероятности. Но рассчитать нормирующую постоянную (p (D)) не получится. Почему? Разберёмся подробнее.
Предположим, H принимает только 3 значения:
p(D) = p(H=H1).p(D|H=H1) + p(H=H2).p(D|H=H2) + p(H=H3).p(D|H=H3)
В таком случае p(D) подсчитать легко. А что, если значение H непрерывно? Получилось бы ли рассчитать это так же легко, особенно если H принимала бесконечные значения? Для этого пришлось бы решить сложный интеграл.
Мы хотим сделать случайный отбор из апостериорного распределения, но также хотим считать p(D) константой.
Методы Монте-Карло с цепями Маркова — это класс алгоритмов для выборки из распределения вероятностей, основанный на построении цепи Маркова, которая в качестве стационарного распределения имеет желаемый вид. Состояние цепи после ряда шагов затем используется в качестве выборки из желаемого распределения. Качество выборки улучшается с увеличением количества шагов.
Разберёмся на примере. Допустим, нужна выборка из бета-распределения. Его плотность:
где C — нормирующая постоянная. На самом деле это некоторая функция от α и β, но я хочу показать, что для выборки из бета-распределения она не нужна, поэтому мы примем ее за константу.
Задача с бета-распределением действительно сложная, если не сказать практически неразрешимая.
В действительности вам, вероятно, придётся работать с более сложными функциями распределения, а иногда вы не будете знать нормирующие постоянные.
Методы MCMC облегчают жизнь, предоставляя алгоритмы, которые могли бы создать цепь Маркова, которая в качестве стационарного распределения имеет бета-распределение, учитывая, что мы можем выбирать из равномерного распределения (что относительно просто).
Если начнём со случайного состояния и перейдём к следующему состоянию на основе некоторого алгоритма несколько раз, мы в конечном итоге создадим цепь Маркова, у которой в качестве стационарного распределения будет бета-распределение. А состояния, в которых мы окажемся через долгое время, могут использоваться как выборка из бета-распределения.
Один из таких MCMC-алгоритмов — алгоритм Метрополиса-Гастингса.
Алгоритм Метрополиса-Гастингса
Интуиция:
Интуитивно понятно, что мы хотим ходить по некоторой кусочной поверхности (нашей цепи Маркова) таким образом, чтобы количество времени, которое мы проводим в каждом местоположении, было пропорционально высоте поверхности в этом месте (желаемая плотность вероятности, из которой хотим сделать выборку).
Так, например, мы хотели бы провести вдвое больше времени на вершине холма высотой 100 метров, чем на соседнем 50-метровом холме. Хорошо, что мы можем сделать это, даже если не знаем абсолютных высот точек на поверхности: все, что нужно знать, это относительные высоты. Например, если вершина холма A в два раза выше вершины холма B, то мы бы хотели провести в A вдвое больше времени, чем на B.
Существуют более сложные схемы предложения новых мест и правил их принятия, но основная идея заключается в следующем:
Цель MCMC — выборка из некоторого распределения вероятностей без необходимости знать его точную высоту в любой точке (не нужно знать C).
Если процесс «блуждания» настроен правильно, вы можете убедиться, что эта пропорциональность (между проведенным временем и высотой распределения) достигнута.
Алгоритм:
Теперь давайте определим и опишем поставленную задачу более формально. Пусть s = (s1, s2,…, sM) — желаемое стационарное распределение. Мы хотим создать цепь Маркова с таким стационарным распределением. Начнем с произвольной цепи Маркова с M-состояниями с матрицей перехода P, так, что pij представляет вероятность перехода из состояния i в j.
Интуитивно мы знаем, как бродить по цепи Маркова, но цепь Маркова не имеет требуемого стационарного распределения. Эта цепь имеет некоторое стационарное распределение (которое нам не нужно). Наша цель — изменить способ, которым мы блуждаем по цепи Маркова, чтобы цепь имела желаемое стационарное распределение.
После большого количества испытаний эта цепь будет сходиться и иметь стационарное распределение s. Затем мы можем использовать состояния цепи как выборку из любого распределения.
Проделывая это для выборки бета-распределения, единственный раз, когда приходится использовать плотность вероятности, — это поиск вероятности принятия решения. Для этого делим sj на si (то есть нормирующая постоянная C сокращается).
Выборка из бета-распределения
Теперь перейдём к проблеме выборки из бета-распределения.
Бета-распределение — непрерывное распределение на [0,1] и может иметь бесконечные значения на [0,1]. Предположим, что произвольная цепь Маркова P с бесконечными состояниями на [0,1] имеет переходную матрицу P такую, что pij = pji = все элементы в матрице.
Нам не нужна Матрица P, как мы увидим позже, но я хочу, чтобы описание проблемы было максимально приближено к алгоритму, который мы предложили.
Метод Монте Карло – что это в экономике, примеры
Метод Монте Карло используется для решения различных задач, где результат зависит от случайных процессов. В частности, метод широко используется в экономике, инвестиционных прогнозах и инвестиционном анализе, финансовом планировании. Моделирование по методу Монте Карло позволяет вычислить множество значений. Используя эти значения, определяется искомый результат путем вычисления среднего арифметического или диапазон, в котором может находиться нужный результат.
В этой статье мы расскажем, как применяется метод Монте Карло в экономике, личных финансах и инвестировании. С помощью наглядных примеров попытаемся понять, какие задачи можно решать с применением метода Монте Карло.
Что такое метод Монте Карло (ММК)
Итак, метод Монте Карло позволяет рассчитать какую-либо величину (или диапазон значений) с использованием множества случайных величин.
К примеру, бегун способен пробежать дистанцию в 10 км за 50 мин. Означает ли это, что 20 км он пробежит за 1 час 40 минут? Конечно же, нет: человек – не машина. Если 10 км можно пробежать без остановки, то расстояние вдвое больше требует значительных затрат энергии. Так, необходимо замедлиться, чтобы попить воды, завязать шнурки. При сильном учащении пульса – перейти на шаг или легкий бег и т.д.
Таким образом, прогнозирование времени путем простых математических расчетов – способ, который даст весьма неточный результат. Правильнее будет отобрать в случайном порядке результаты забегов нескольких спортсменов (чем больше, тем лучше) такого же пола, примерно того же возраста и уровня подготовки, которые несколько раз бежали дистанции по 20 км, и вычислить среднее арифметическое результатов. Тогда мы получим значение, на которое можно ориентироваться.
Примерно так работает метод Монте Карло простыми словами. С помощью метода можно вычислять риски. Возвращаясь к нашему примеру, подумаем, какова вероятность того, что спортсмен не пробежит 20 км? Причин может быть масса: внезапная травма, сильная усталость, ситуация на дороге и т.д. Это те самые случайные события, определить вероятность которых невозможно, т.к. они все разные по своей природе. Если все же пользоваться какими-то примерными цифрами или диапазонами значений, то, скорее всего, мы получим такой результат, о котором математики говорят: «задача не имеет решений».
Поэтому следует ориентироваться только на имеющиеся данные, полученные в результате коллективных забегов, когда имели место подобные случаи. Выбрав несколько результатов и сопоставив их с количеством бегунов, пробежавших дистанцию успешно, мы получим средний процент риска.
Для прогнозирования рисков, доходности, сроков окупаемости и других финансовых результатов используется метод Монте-Карло-симуляции. Вероятность события определяется так: программа выбирает комбинации случайных значений (например, неблагоприятных исходов) и на основании этого выдает усредненный результат. Для получения более точного значения симуляцию следует повторить несколько раз. Программное обеспечение применяется различное – от знакомого нам всем Excel до узкоспециализированных программных продуктов, используемых финансовыми аналитиками, физиками, программистами, трейдерами и др.
История
Откуда метод получил свое название? В Европе есть маленькое княжество Монако, где одна из территорий названа Монте-Карло. Это такой европейский Лос-Анджелес, где можно окунуться в роскошь и азартные развлечения. От знаменитого казино метод Монте-Карло получил свое имя.
Впервые о методе заговорили в конце 40-х годов прошлого столетия, когда ВВС США начало разработку водородной бомбы. Тогда, с появлением первых ЭВМ, было предложено использовать теорию вероятностей для решения прикладных задач.
Далее, в 1970-х годах, метод получил применение в нейтронной физике для задач, не поддающихся решению традиционными математическими методами. Впоследствии моделирование по методу Монте-Карло распространилось на другие области физики, а также на экономику и вычислительную математику.
Схема метода
Имитационное моделирование по методу Монте-Карло представляет собой определение математического ожидания (среднего значения случайной величины) путем проведения определенного количества симуляций (испытаний).
Предположим, требуется найти математическое ожидание α для случайной величины \( X \) :
Классическая формула расчета математического ожидания выглядит так:
\( x1…n \) – значение величины от 1 до n;
\( p1…n \) – вероятность от 1 до n.
Моделирование методом Монте-Карло выполняется следующим образом: проводится n симуляций (испытаний). В результате получится какое-то количество значений X. Далее определяется их среднее арифметическое, которое и будет приблизительным значением α.
Зачем нужен ММК и где он применяется
Чтобы не углубляться в математические дебри, сформулируем кратко суть метода.
Метод Монте-Карло относится к методам моделирования различных явлений, событий, параметров или процессов, как благоприятных, так и неблагоприятных, с целью определения вероятности их наступления. Для этого генерируется определенное количество случайных величин, отвечающих установленным критериям, а затем на их основе вычисляют приблизительное значение искомой величины.
ММК применяется в следующих областях:
По сути, методу можно найти применение во многих сферах, где необходимы расчеты и прогнозирование.
Входные данные
Данные для получения искомой величины определяются путем стохастической (случайной) выборки. Чтобы было более понятно, приведем простейший пример из компьютерных игр.
Предположим, у нас есть компьютерная игра, в которую мы играли много-много раз. При этом ведется статистика: сыграно 100 игр, из них 30 побед, 70 поражений. Это и будет нашими входными данными. А решение будет таким: вероятность победы – 30%, проигрыша – 70%.
Можно использовать метод Монте-Карло для симуляции инвестиционного портфеля. Предположим, нам нужно получить доходность не менее 10%. Для этого подбираем инструменты с доходностью не меньше этой величины и вычисляем среднее арифметическое. Составляющие портфеля можно варьировать для получения максимальной доходности. Здесь входными данными будут наименование, стоимость и доходность отдельного инструмента, а искомым значением – общая доходность портфеля.
Процесс моделирования методом Монте-Карло
Имитационное моделирование методом Монте-Карло – это автоматизированный процесс, позволяющий рассматривать вероятность наступления различных событий. Каждая смоделированная ситуация является уникальной, что дает возможность оценить целый спектр рисков.
При создании модели все неопределенные факторы заменяются диапазоном возможных значений. К примеру, ни один аналитик, занимающийся оценкой рисков, не может знать, каким будет курс евро через 3-5 лет. Программа позволяет задать диапазон значений на усмотрение специалиста. Разумеется, здесь многое зависит от человека: требуется определенный уровень квалификации.
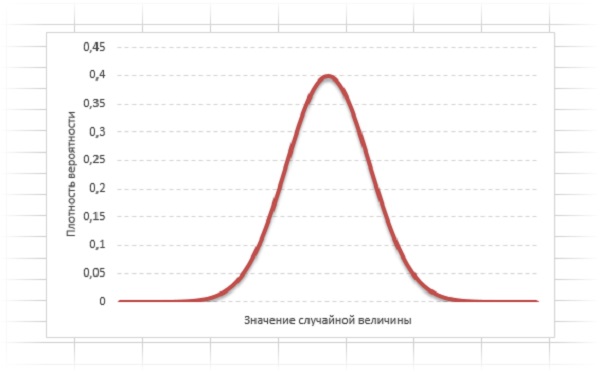
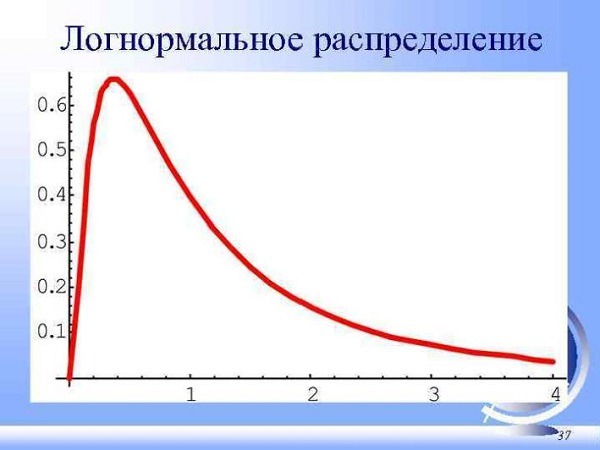
Далее система распределяет вероятности. Для оценки различных параметров применяются варианты распределения:
Значение случайной величины, расположенное посередине, характеризует наиболее высокую вероятность. Для построения кривой используются статистические данные: ожидаемое значение и стандартное отклонение. Такой вариант распределения подойдет, к примеру, для расчета стоимости коммунальных услуг в обозримом будущем.
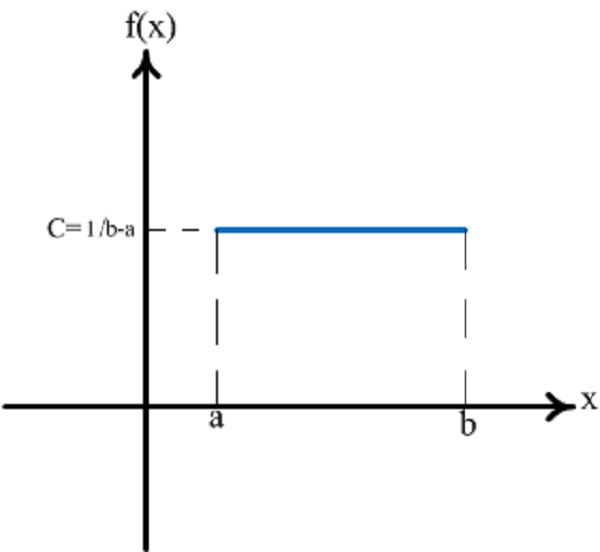
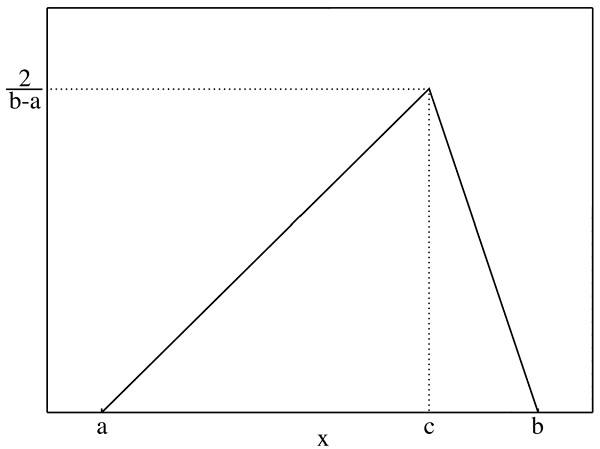
Кривая равномерного распределения имеет вид прямоугольника. На графике a и b – минимальные значения, С – вероятность. Подойдет для расчета условно-постоянных расходов в краткосрочном периоде.
Итак, имитационное моделирование по методу Монте-Карло выполняется многократно. По результатам всех операций делается выборка значений, результаты систематизируются и определяется итоговая вероятность события.
Выходные данные
Выходными или итоговыми данными имитационного моделирования по методу Монте-Карло могут быть числовые значения или проценты. В отдельных случаях значения могут находиться внутри диапазона.
Однако итоги тестирования выражаются не только в цифрах. Возможно также выявление каких-то функций или параметров в модели, которые оказывают наибольшее влияние на результат. К примеру, наибольшее влияние на курс рубля оказывают цены на нефть на мировом рынке.
Сколько имитационных испытаний необходимо выполнить
Количество симуляций зависит от цели исследования. Как уже упоминалось, моделирование повторяется сотни, тысячи, иногда десятки тысяч раз – чем больше испытаний, тем более достоверный результат будет получен на выходе. При наличии программы не возникает проблем в многократном повторении операции.
Преимущества и недостатки метода
Достоинствами ММК являются:
Примеры
Перейдем к практическим примерам использования метода Монте-Карло.
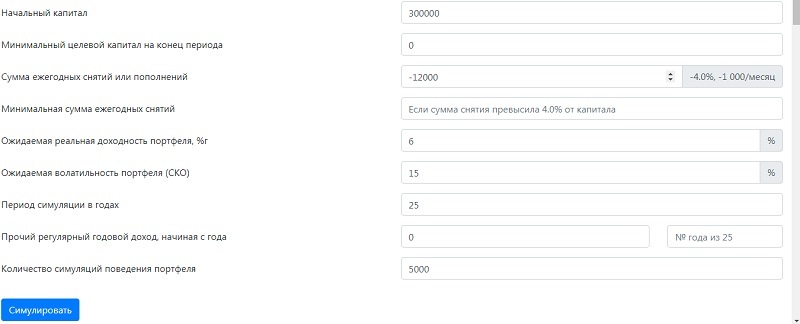
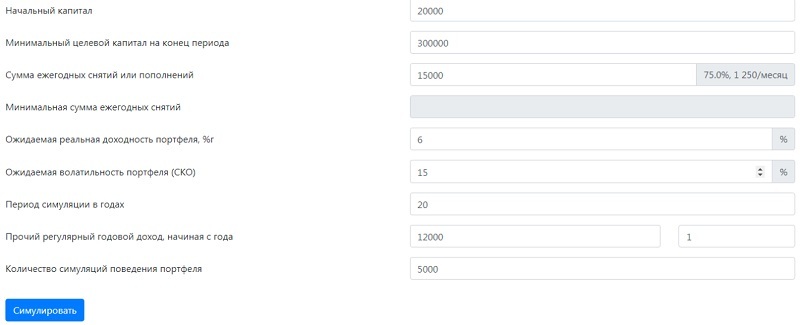
Пример 1. Рассмотрим ситуацию, когда 35-летний человек планирует уйти на пенсию в 60 лет.
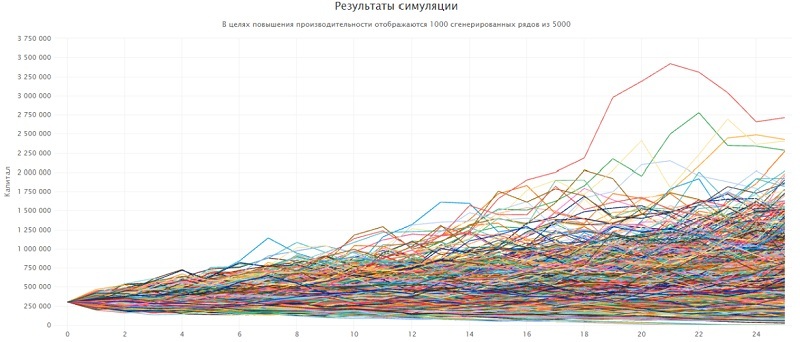
Таким образом, цель – накопить 300000$ (1000х12/0.04). Проверим вероятность этой суммы, используя симулятор. Программа выполнит 125000 симуляций (5000х25 лет).
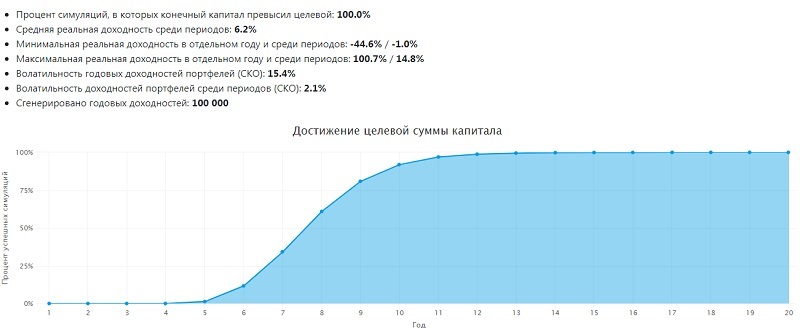
Итак, по первой строчке мы видим, что в 99,7% симуляций цель будет выполнена.
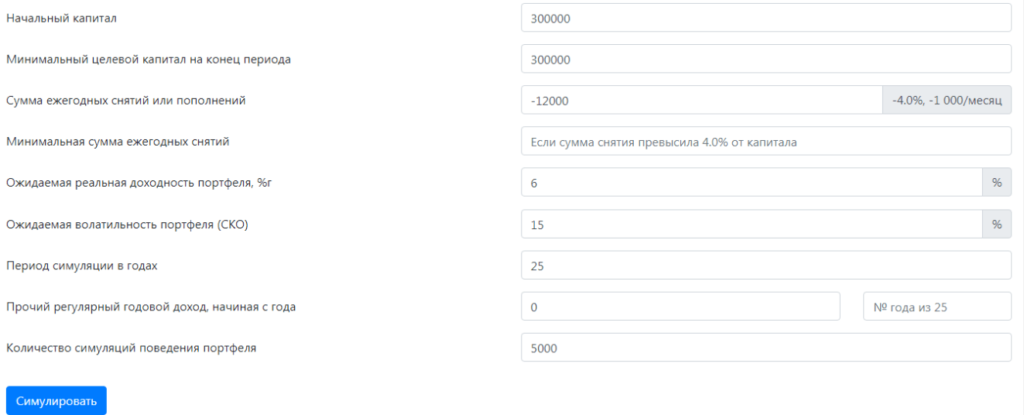
Пример 2. При тех же условиях зададим размер капитала, который мы планируем сохранить на конец периода. Для удобства примем эту сумму равной размеру начального капитала.
Здесь процент вероятности благоприятного развития событий уменьшился до 84,3%. Что с этим можно сделать?
Когда я смогу накопить
Метод Монте-Карло является примером подхода к моделированию на основе результатов анализа взаимосвязей между явлениями. В наших примерах эту взаимосвязь можно охарактеризовать так: доходность инвестиций → инфляция → волатильность портфеля → капитал.
Не стоит забывать и о том, что в любую модель могут вноситься коррективы под влиянием воли человека. Причиной тому могут быть непредвиденные обстоятельства, которые случаются в жизни каждого, а уж за анализируемый нам 25-летний период их будет немало. Тем не менее, рассмотрим «обратный» пример, где цель – не сохранить, а наоборот, накопить тот самый капитал в 300000$, необходимый для того, чтобы обеспечить безбедную старость.
Из графика видно, что нужная сумма накопится примерно на 13-м году. Не следует забывать о падениях рынка, которые случаются раз в несколько лет. Вместе с тем, некоторые активы могут взлететь в цене, что принесет крупный незапланированный доход. Но ориентироваться лучше на срок с запасом в 2-3 года, т.е. примерно 15-16 лет с точки отсчета.
Заключение
Мы разобрали метод Монте-Карло от самых простых основ, «для чайников», до описания зависимостей между процессами и примеров имитаций с помощью программных средств. Углубляться в математические функции и вспоминать теорию вероятности не стоит, тем более что мало кто в наше время будет заниматься моделированием вручную.
Достаточно понять, что метод Монте-Карло основан на моделировании случайных процессов на основании заданных пользователем исходных данных. ММК успешно применяется там, где обычные математические расчеты могут дать недостоверные результаты.
Предусмотреть все случайности с вероятностью 100% сложно, поэтому метод допускает определенную погрешность, которая частично компенсируется количеством произведенных симуляций.