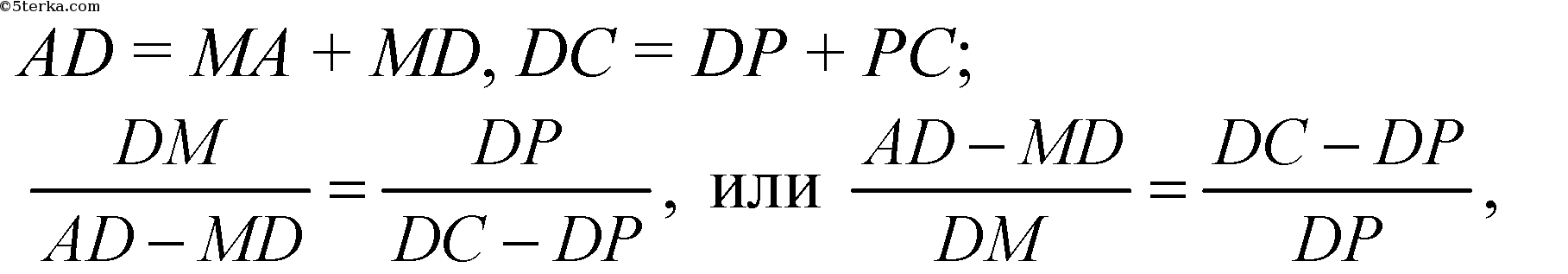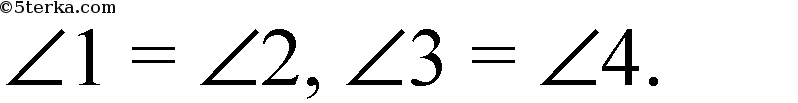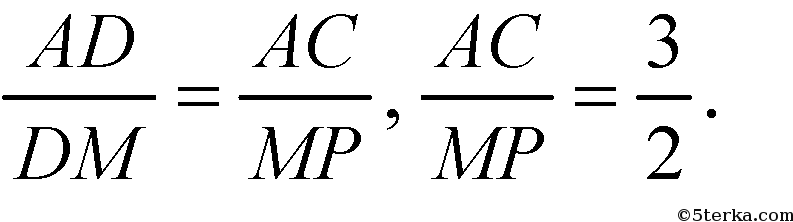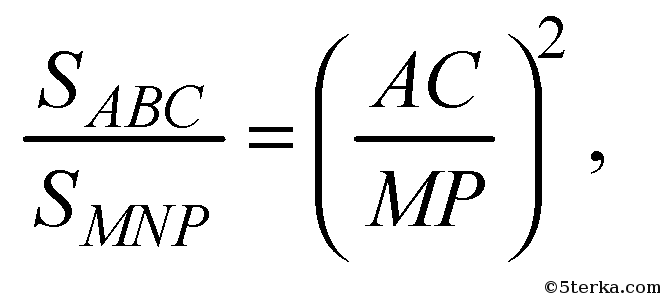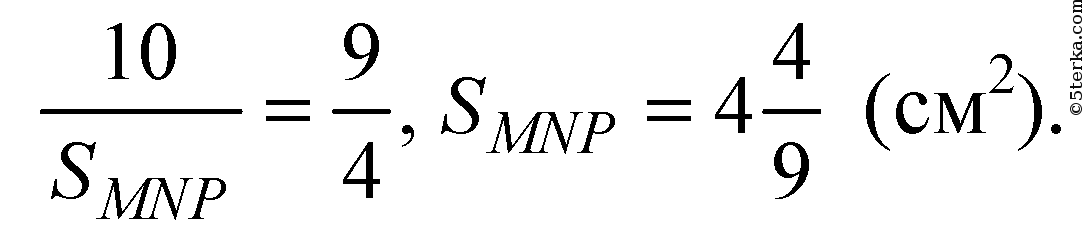на ребрах да дв и дс тетраэдра давс отмечены точки м н п так что
103. На ребрах DA, DB и DC тетраэдра DABC отмечены точки М, N и Р так, что DM:MA = DN:NB = DP:PC. Докажите, что плоскости MNP и ABC параллельны. Найдите площадь треугольника MNP, если площадь треугольника ABC равна 10 см2 и DM: МА = 2:1.
Рассмотрим ΔADC и ΔMDP.
Из подобия следует:
Из равенства углов получим, что МР || AC.
Аналогично, для грани DCB, имеем, что PN || CB.
Итак, MP || AC и PN || CB. По теореме п. 10 пл. MNP || пл. ABC. ΔMNP
ΔABC (по двум углам).
т.к. площади подобных фигур относятся как
квадраты линейных размеров.
В тетраэдре ДАВС точки M, N и P – середины рёбер ДА, ДВ, ДС соответственно. а) Доказать, что плоскости (MNP) и (АВС) параллельны. б) Найти площадь ∆ АВС, если S∆MNP = 14 см2
помогите пожалуйста ни как решить не могу
Лучший ответ по мнению автора
а) 1) NP — средняя линия треугольника DCB, следовательно, NP || BC (по свойству средней линии треугольника: средняя линия треугольника параллельна стороне и равна ее половине)
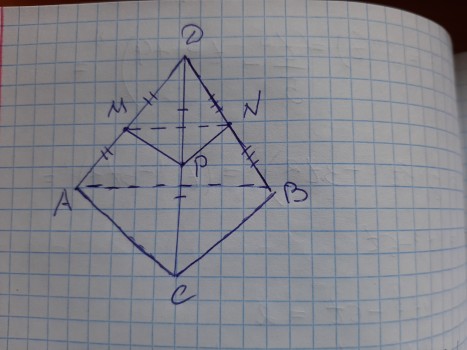
MP — средняя линия треугольника АDC, следовательно, MP || AC
2) Используя признак параллельности плоскостей (Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости, то такие плоскости параллельны), получаем:
MP || AC, NP || BC и МР пересекает NP и АС пересекает BC, следовательно, (MNP) || (ABC), ч. т. д.
б) 1) NP = 1/2 BC |
MP = 1/2 AC | (по свойству средней линии треугольника), следовательно, P (MNP) = 1/2 * ( AB + AC + BC) =
MN = 1/2 AB |
= 1/2 P (ABC), т. е. k = Р(MNP) / P(ABC) = 1/2 (где k — коэффициент подобия треугольников)
2) S(MNP) / S(ABC) = k^2 (свойство подобных треугольников: отношение площадей подобных треугольников равно квадрату коэффициента подобия), т. е. получаем:
14 / S(ABC) = 1/4
Перемножаем пропорцией:
S(ABC) = 14 * 4 = 56 см^2
Ответ: а) ч. т. д.; б) S(ABC) = 56 см^2
На ребрах да дв и дс тетраэдра давс отмечены точки м н п так что
Точки М, N и К принадлежат соответственно ребрам АD, AB и BC тетраэдра ABCD,
а) Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K.
б) Найдите отношение, в котором секущая плоскость делит ребро CD.
а) Продлим 
до пересечения с 
в точке 
Обозначим точку пересечения 
и 
за 
Тогда 
искомое сечение.
б) Из теоремы Менелая для треугольника ABC: 
Откуда следует, что CQ = CA.
Из теоремы Менелая для треугольника ADC: 
Из чего следует, что DP : PC = 3:1.
Приведем другое решение пункта б).
Напомним теорему Менелая для тетраэдра: точки A, P, N и K, лежащие на ребрах тетраэдра AD, DC, AB и BC соответственно, принадлежат одной плоскости тогда и только тогда, когда 
В нашем случае: 
откуда 