найдите все простые р для которых число р2 14 так же будет простым числом

math4school.ru

Простые и составные числа

Немного теории

Простое число – это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя. Все остальные натуральные числа, кроме единицы, называются составными. Таким образом, все натуральные числа больше единицы разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел.

Приведём некоторые свойства простых чисел.

Основная теорема арифметики. Каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей.

Простых чисел бесконечно много.

Если p – простое, и p делит a·b, то p делит a или b.

Mалая теорема Ферма. Если p – простое, a – натуральное, то a p – a делится на p.

Теорема Вильсона. Натуральное p > 1 является простым тогда и только тогда, когда (p – 1)! + 1 делится на p.

Постулат Бертрана. Если n > 1 – натуральное, то существует простое p, такое, что n 1 – целые взаимно простые числа, содержит бесконечно много простых чисел.

Теорема Ферма. Каждое простое число вида 4k + 1 есть сумма двух квадратов натуральных чисел.

Всякое простое число, большее 3, представимо в виде 6k + 1 или 6k – 1, где k – некоторое натуральное число.

Число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, большим 2.

Число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, большим 1.

Задачи с решениями

1. Три простых числа, каждое из которых больше 10, образуют арифметическую прогрессию. Докажите, что разность прогрессии делится на 6.

Все данные простые числа нечётные, поэтому их разность делится на 2. Покажем, что она делится и на 3. Пусть данные числа a, a + d, a + 2d. Ни одно из них не делится на 3, поэтому при делении на 3 даёт остаток или 1, или 2. Следовательно, по крайней мере, два из этих чисел дают при делении на 3 одинаковые остатки. Разность этих чисел, равная d или 2d, делится на 3. Поскольку 2 на 3 не делится, то d делится на 3. Итак, разность прогрессии, которая делится на взаимно простые числа 2 и 3, делится на 6, что и требовалось доказать.

2. Докажите, что для произвольного натурального числа n найдётся натуральное m такое, что nm + 1 – составное число.

Можно выбрать m = n + 2, тогда

nm + 1 = n(n + 2) + 1 = n 2 + 2n + 1 = (n + 1) 2

является составным числом.

3. Найдите все целые числа n, для которых модуль значения трёхчлена n 2 – 7n + 10 будет простым числом.

|n 2 – 7n + 10| = |n –2| · |n – 5|,

то следует искать такие n при которых один из множителей последнего произведения равен 1, а второй является простым числом. Этому требованию удовлетворяют n = 3 и n = 4.

4. Докажите, что если числа

а) m и m 2 + 2 простые, то число m 3 + 2 тоже простое;

б) р, р – 10, р + 10 простые, то число р – 2 тоже простое.

а) Любое простое число m, отличное от 3, можно представить в виде 3n+1 или в виде 3n–1, где n – некоторое натуральное число. В первом случае можно записать

m 2 + 2 = 9n 2 + 6n +3,

m 2 + 2 = 9n 2 – 6n +3,

Так как m > 2, то в любом случае число m 2 +2 больше 3 и делится на 3, а значит является составным. Следовательно, число m 2 +2 может быть простым, только если m = 3. В этом случае m 2 +2 = 11 – простое число, m 3 +2 = 29 – тоже простое число, что и требовалось доказать.

б) Так как р – 10 = (р – 1) – 9 и р + 10 = (р + 1) + 9, то числа р – 10 и р – 1 при делении на 3 имеют одинаковые остатки, и числа р + 10 и р + 1 при делении на 3 имеют одинаковые остатки.

Из трёх последовательных чисел р – 1, р, р + 1 одно и только одно делится на 3. С учётом выше сказанного, то же утверждение верно для чисел р – 10, р, р + 10. Так как эти числа простые, то р – 10 = 3 и р = 13, поэтому р – 2 = 11 – простое число, что и требовалось доказать.

5. Сколько раз входит двойка в разложение на простые множители произведения

Ответ на поставленный вопрос получим из следующих преобразований:

6. Найдите все простые p такие, что число p 2 + 11 имеет ровно 6 различных делителей (включая единицу и само число).

Если p > 5 и простое, то числа p – 1 и p + 1 оба четные, и одно из них кратно трем. Поэтому произведение (p – 1)(p + 1) делится на 12, следовательно, p 2 + 11 также делится на 12, а значит, имеет не менее семи делителей (6 делителей числа 12 и само число p 2 + 11 > 12 ). Осталось проверить p = 2 и p = 3.

Если p = 2, то p 2 + 11 = 2 2 + 11 = 15 имеет 4 делителя (1, 3, 5, 15).

Если p = 3, то p 2 + 11 = 3 2 + 11 = 20 имеет 6 делителей (1, 2, 4, 5, 10, 20).

7. Найти все натуральные числа n, для которых каждое из шести чисел

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

Рассмотрим варианты. Для n = 1 число n + 3 = 4 составное.

Для n = 2 число n + 7 = 9 составное.

Для n = 3 число n + 1 = 4 составное.

Для n > 4 все наши числа больше 5 и по крайней мере одно из них делится на 5, так как числа 1, 3, 7, 9, 13 и 15 при делении на 5 дают соответственно остатки 1, 3, 2, 4, 3 и 0, то есть все возможные остатки, откуда следует, что и числа

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

при делении на 5 дают все возможные остатки и, следовательно, хотя бы одно из них делится на 5 и как число, большее пяти (так как n > 4), является составным.

Но для n = 4 мы получаем простые числа 5, 7, 11, 13, 17 и 19.

8. Доказать, что каждое простое число вида 4k + 1 является длиной гипотенузы прямоугольного треугольника, стороны которого выражаются натуральными числами.

9. Сколькими способами можно раскрасить круг, разбитый на р равных секторов с помощью n красок, если р – простое число и каждый сектор раскрашиваем одной краской? Две раскраски, совпадающие при повороте круга, считаем одинаковыми.

Каждый сектор можно раскрасить в любой из n цветов, поэтому для круга с р секторами получим n p раскрасок, среди которых (n p – n) не одноцветных. Каждая из этих раскрасок поворотами переходит в (р – 1) одинаковую с ней, значит, существенно различных не одноцветных раскрасок будет (n p – n)/p, откуда общее число раскрасок равно n + (n p – n)/p.

10. Доказать, что для любого простого числа p > 5 уравнение х 4 + 4 x = p в целых числах не имеет решений.

Докажем, что если для некоторого целого значения х число

является целым, то это число либо не превосходит пяти, либо является составным.

Действительно, если х 4 + 4 0 4 + 4 1 = 5.

Если x = 2k (k – натуральное число), то число

f(x) = 2 4 k 4 + 4 2k = 2 4 ( k 4 + 4 2(k–1) )

Наконец, если x = 2k + 1 (k – натуральное число), то число

f(x) = x 4 + 4·4 2k = (x 4 + 4x 2 (2 k ) 2 + 4(2 k ) 4 ) – 4x 2 (2 k ) 2 =

= (x 2 + 2(2 k ) 2 ) 2 – (2·x·2 k ) 2 =

= (x 2 + 2·x·2 k + 2(2 k ) 2 )·( x 2 – 2·x·2 k + 2(2 k ) 2 ) =

= ((x + 2 k ) 2 + 2 2k )·((x – 2 k ) 2 + 2 2k )

так же является составным, поскольку каждый из двух сомножителей последнего произведения больше 1 (ибо 2 2k > 1 при k > 0).

Таким образом, если число p > 5 простое, то равенство х 4 + 4 x = p не выполняется ни при каких целых значениях х.

Задачи без решений

1. Известно, что р, р + 10, р + 14 – простые числа. Найдите число р.

2. Докажите, что число

3. Найдите все простые р для которых число р 2 + 14 так же будет простым числом.

4. Докажите, что уравнение х 2 + х + 1 = р·у имеет решение в целых числах (х, у) для бесконечного числа простых р.

5. Введём обозначение для суммы первых n простых чисел через S_n:

Докажите, что между числами S_n и S_n+1 всегда существует число, являющееся полным квадратом.

Источник

Найдите все простые р для которых число р2 14 так же будет простым числом

Задача 85:

Пусть ka ≡ kb (mod %)%m, k и m – взаимно просты. Тогда a ≡ b (mod %)%m.

Решение:

Поскольку ka ≡ kb (mod %)%m, то ka – kb = k(a – b) делится на m. Так как k и m взаимно просты, то a – b делится на m, т.е. a ≡ b (mod %)%m.

Задача 86:

Пусть ka ≡ kb (mod kn). Тогда a ≡ b (mod %)%n.

Решение:

ka – kb делится на kn, т.е. k(a – b) = mkn. Следовательно, a – b = mn, ч.т.д.

Задача 87:

Найдите остаток от деления 2¹ºº на 101.

Решение:

Вследствие малой теоремы Ферма, он равен 1.

Задача 88:

Найдите остаток от деления 3¹º² на 101.

Решение:

Так как 101 – простое число, то 3¹ºº ≡ 1 (mod 101). Отсюда 3¹º² ≡ 9 • 3¹ºº = 9 (mod 101).

Задача 89:

Докажите, что 300³ººº – 1 делится на 1001.

Решение:

300³ººº = (300 500 ) 6 ≡ 1 (mod 7). Аналогично, 300³ººº ≡ 1 (mod 11) и (mod 13). Следовательно, 300³ººº – 1 делится и на 7, и на 11, и на 13, т.е. на 1001.

Задача 90:

Найдите остаток от деления 8 900 на 29.

Решение:

Задача 91:

Докажите, что 7¹²º – 1 делится на 143.

Решение:

Докажем, что 7¹²º – 1 делится на 11 и на 13. Действительно, (7¹²)¹º ≡ 1 (mod 11) и (7¹º)¹² ≡ 1 (mod 13).

Задача 92:

Докажите, что число 30 239 + 239³º – составное.

Решение:

Это число делится на 31.

Задача 93:

Пусть p – простое число. Докажите, что (a + b) p = a p + b p (mod %)%p для любых целых a и b.

Решение:

(a + b) p ≡ (a + b) = a + b ≡ a p + b p (mod p).

Задача 94:

Сумма трех чисел a, b и c делится на 30. Докажите, что a 5 + b 5 + c 5 также делится на 30.

Решение:

Докажите, что для произвольного целого x верно сравнение x 5 ≡ x (mod 30).

Задача 95:

Пусть p и q – различные простые числа. Докажите, что

а) p q + q p = p + q (mod pq).

б) 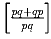– четное число, если p, q ≠ 2.

Решение:

Докажите, что p q + q p – p – q делится и на p, и на q.

Задача 96:

Пусть p – простое число, и a не делится на p. Докажите, что найдется натуральное число b, для которого ab ≡ 1 (mod p).

Решение:

Задача 97:

(Теорема Вильсона). Пусть p – простое число. Докажите, что (p – 1)! ≡ – 1 (mod %)%p.

Задача 98:

Пусть n – натуральное число, не кратное 17. Докажите, что либо n 8 + 1, либо n 8 – 1 делится на 17.

Решение:

(n 8 + 1)(n 8 – 1) = n 16 – 1 = 0 (mod 17).

Задача 99:

а) Пусть p – простое число, отличное от 3. Докажите, что число 111 … 11 (p единиц) не делится на p.

б) Пусть p > 5 – простое число. Докажите, что число 111 … 11 (p – 1 единица) делится на p.

Решение:

а) 111 … 11 (p единиц) = (10 p – 1)/9, а 10 p – 1 не делится на p, так как 10 p – 1 ≡ 10 – 1 = 9 (mod p).

б) 111 … 11 (p – 1 единица) = (10 p – 1 – 1)/9, а 10 p – 1 – 1 делится на p, так как p взаимно просто с 10 и с 9.

Задача 100:

Докажите, что для любого простого p разность 111 … 11222 … 22333 … 33 … 888 … 88999 … 99 – 123456789 (в первом числе каждая ненулевая цифра написана p раз) делится на p.

Решение:

Воспользуйтесь тем, что 10 p ≡ 10 (mod p), 10 2p ≡ 100 (mod p), …, 10 8p ≡ 10 8 (mod p).

Источник

Задачи с решениями. Простые числа

Задачи с решениями. Простые числа. Предлагается 15 задач с подробными решениями.

Просмотр содержимого документа
«Задачи с решениями. Простые числа»

Задачи с решениями. Простые числа

Решение:

Решение:

3.Может ли сумма двух простых чисел быть простым числом?

Решение: Да, может, но при условии, что одно из этих чисел будет равно 2, иначе мы получим сумму двух нечётных чисел, которая в результате будет чётным числом, следовательно, делится на 2 и не является простым.

4.Может ли сумма двух последовательных натуральных чисел быть простым числом?

Решение: 2+3=5, 3+4=7, 5+6=11, 6+7=13, 8+9=17; 5, 7, 11, 13, 17 – простые числа;

Попробуем показать это в общем виде:

Пусть n и n+1 два последовательных натуральных числа, значит одно из них чётное и делится на 2. Тогда их сумма будет равна n+n+1 = 2n+1.

Если n2 и n – чётное, то после сокращения n на 2 получится число, большее одного. Тогда данная сумма будет равна произведению двух чисел, больших 1 и меньших её самой (одно из них – это (n+1), другое то, что получилось после сокращения n на 2). Значит, эта сумма не может быть простым числом, так как имеет делители, отличные от 1 и самой себя.

Аналогично рассматривается случай, когда n2 и n – нечётное. (В этом случае, (n+1) – чётное и большее 2.)

Остались два возможных случая: n=1 и n=2. Если n=1, то сумма будет равна 2n+1 = 2?1+1 = 3 – простое число. Если n=2, то 2n+1= 2?2+1=5 – тоже простое число.

Ответ. На основании этого можно сказать, что сумма двух последовательных натуральных чисел может оказаться простым числом

5.Может ли сумма трёх последовательных натуральных чисел быть простым числом?

Решение: Проведём рассуждения в общем виде:

Пусть n, n+1и n+2 – три последовательных натуральных числа, тогда их сумма равна n+(n+1)+(n+2) = 3n+3 = 3(n+1), т.е. всегда делится на 3, следовательно, составное число.

Ответ. Нет, не может, т.к. полученная сумма является составным числом.

6.Может ли сумма четырех последовательных натуральных чисел быть простым числом?

Решение: Пусть n, n+1и n+2 и n+3 – четыре последовательных натуральных числа, тогда их сумма равна n+(n+1)+(n+2)+( n+3) = 4n+6 = 2(2n+3), т.е. всегда делится на 2, следовательно, составное число.

Ответ. Нет, не может, т.к. полученная сумма является составным числом.

7.Может ли любое натуральное число быть представлено в виде произведения простых чисел?

Решение: Разложим число n, где n – составное число и 16≤ n

Вывод: Из данного разложения замечаем, что любое указанное n может быть представлено в виде произведения, не более трёх простых множителей.

Возникает вопрос: любое ли натуральное число представимо в виде произведения простых множителей?

Ответ на поставленный вопрос даёт основная теорема арифметики:

Всякое натуральное число n1 либо просто, либо может быть представлено, и притом единственным образом, в виде произведения простых множителей.

8.Может ли площадь квадрата, длина стороны которого выражена натуральным числом, быть простым числом?

Ответ. Нет, не может.

9.Клиент банка забыл четырёхзначный шифр своего сейфа и помнил лишь, что этот шифр – простое число, а произведение его цифр равно 243. За какое наименьшее число попыток он наверняка сможет открыть свой сейф.

Решение: Пусть abcd – искомое число. Разложим число 243 на простые множители: 243 = 3?3?3?3?3. Тогда возможны несколько случаев:

243 = 3?3?3?9, но тогда число, составленное из этих цифр будет делиться на 3 (по признаку делимости, сумма цифр равна 18, а 18 делится на 3), значит оно составное;

Из четырех цифр 1,3,9,9 можно составить следующие комбинации: 1399, 1993, 1939, 3991, 3199, 3919, 9139, 9193, 9319, 9391, 9913, 9931. По условию задачи числа должны оказаться простыми. Пользуясь таблице простых чисел, оставляем только простые числа: 1993, 1399, 3919, 9931, 9319, 9391. Остаётся 6 простых чисел, это и есть число попыток, за которое клиент банка сможет открыть сейф.

Ответ. За 6 попыток.

10..Вася умножил некоторое число на 10 и получил простое число. А Петя умножил то же самое число на 15, но всё равно получил простое число. Может ли быть так, что никто из них не ошибся?

Решение: 0,2· 10 = 2 и 0,2·15 = 3 – простые числа.

11.Четверо ребят обсуждали ответ к задаче. Коля сказал: «Это число 9». Роман: «Это простое число». Катя: «Это четное число». А Наташа сказала, что это число делится на 15. Один мальчик и одна девочка ответили верно, а двое остальных ошиблись. Какой ответ в задаче на самом деле?

Решение

Если Коля ответил верно, то обе девочки ошиблись, так как число 9 нечётное и не делится на 15. Значит, верный ответ дал Роман. Но простое число не делится на 15, а единственное чётное простое число – это 2.

12. Докажите, что для произвольного натурального числа n найдётся натуральное m такое, что nm + 1 – составное число.

Решение: Можно выбрать m = n + 2, тогда

nm + 1 = n(n + 2) + 1 = n 2 + 2n + 1 = (n + 1) 2

является составным числом.

13. Найдите все целые числа n, для которых модуль значения трёхчлена n 2 – 7n + 10 будет простым числом.

Решение: Так как |n 2 – 7n + 10| = |n –2| · |n – 5|,

то следует искать такие n при которых один из множителей последнего произведения равен 1, а второй является простым числом.

Этому требованию удовлетворяют n = 3 и n = 4.

14.Доказать, что каждое простое число вида 4k + 1 является длиной гипотенузы прямоугольного треугольника, стороны которого выражаются натуральными числами.

Замечание. Другие примеры подобных троек можно найти в таблице пифагоровых чисел с наибольшим числом не превосходящим 110 и в таблице примитивных пифагоровых чисел со средними числами, не превосходящими 256.

15.Сколькими способами можно раскрасить круг, разбитый на р равных секторов с помощью n красок, если р – простое число и каждый сектор раскрашиваем одной краской? Две раскраски, совпадающие при повороте круга, считаем одинаковыми.

Решение: Каждый сектор можно раскрасить в любой из n цветов, поэтому для круга с р секторами получим n p раскрасок, среди которых (n p – n) не одноцветных. Каждая из этих раскрасок поворотами переходит в (р – 1) одинаковую с ней, значит, существенно различных не одноцветных раскрасок будет (n p – n)/p, откуда общее число раскрасок равно n + (n p – n)/p.

Источник