рекурсия в жизни человека
Рекурсия вокруг нас: люди, соборы и капуста романеско
Спойлер: рекурсия есть не только в цифровом мире. Встречается она и в реальном. И намного чаще, чем вы думаете, — разная и интересная.
Про рекурсивные функции я узнала на уроках информатики. Потом долго считала рекурсию всего лишь отвлечённым понятием из программирования, далёким от реальной жизни. Почему-то в школе нам не рассказывают, что на самом деле явление это встречается в природе, науке, искусстве, а рекурсивные алгоритмы применимы даже для решения бытовых задач.
Что такое рекурсия
В программировании рекурсивная функция — это такая функция, которая вызывает себя из себя же самой, но с другими значениями параметров.
Примечание. Функция может вызывать себя и через промежуточные функции. Например, функция А запускает функцию Б, а та снова вызывает А.
Цепочка вызовов не может быть бесконечной, она должна прерваться и выдать ответ. Поэтому должен возникать крайний случай (или несколько), когда функции уже не нужно вызывать себя с другими параметрами (то есть погружаться ещё глубже), а можно сразу вернуть результат.
Звучит и правда сложно, но не пугайтесь — с примером станет понятнее.
Классический пример рекурсивной функции — вычисление факториала, то есть произведения натуральных чисел от 1 до N.
Здесь N=0 — это крайний случай: функция ничего не вызывает и сразу возвращает единицу (по определению, факториал нуля равен единице).
В более широком смысле рекурсией называют описание или изображение предмета, объекта, явления внутри самого себя. Рекурсивный принцип — это принцип самовоспроизведения и одновременно усложнения системы по одному и тому же алгоритму.
Тут-то и выясняется, что и нас, людей, тоже можно считать рекурсивными: ведь в клетке заложена информация обо всём организме, в ДНК записана информация о том, как синтезировать ДНК.
Фулстек-разработчик. Любимый стек: Java + Angular, но в хорошей компании готова писать хоть на языке Ада.
Рекурсия — не то же самое, что бесконечный цикл
Хотя её часто с ним путают. Понять разницу проще всего на примере. Предположим, ваш начальник издал приказ:
Это не рекурсия. Просто в ситуации, когда начальник не прав, мы попадём в бесконечный цикл вызовов.
Но можно внести небольшое изменение и получить рекурсию:
Приказ стал рекурсивным, потому что в одной из веток вызывает сам себя.
На обед у нас салат «Рекурсивный»: помидоры, огурцы, салат.
Рекурсию можно увидеть
И это очень красиво. Рекурсивные изображения, они же фрактальные паттерны или просто фракталы, — это рисунки или предметы, которые подобны сами себе: состоят из уменьшенных копий себя.
Подобным же образом выстроены кровеносные сосуды и нервы в организме животных. Свойствами фракталов обладают снежинки, а ещё — удивительная капуста романеско. Вот она на картинке ниже — ну разве не красавица? 😀
В архитектуре рекурсия встречается в облике готических соборов.
В этом соборе XIII века задействован один из характерных для готики приёмов: его окна украшены тонкими ажурными перегородками. Их основной узор — стрельчатая арка с кругом внутри, круг поддерживается двумя арками меньшего размера.
А вот рекурсивная версия того же узора — Собор Линкольна.
Здесь окно тоже выполнено в форме остроконечной арки с вписанным в неё кругом, а круг лежит на двух других арках. Вот только внутри каждой из этих арок — снова круг и две ещё меньших арки, а внутри них — ещё по одному кругу на двух меньших арках.
Другой пример архитектурной рекурсии — собор Святого Петра в Ватикане.
Джордж Херси, американский писатель и журналист, сравнивал его с китайскими шкатулками с секретом. По его словам, архитектурный комплекс состоит из одной макроцеркви, четырёх наборов того, что журналист назвал макси-церквями, 16 мини-церквей и 32 микроцерквей. А мог бы просто сказать, что собор рекурсивный.
В изобразительном искусстве рекурсия тоже отметилась — взять хотя бы «Триптих Стефанески» Джотто. На его центральной панели изображён кардинал Стефанески, которой держит в руках этот же триптих (на котором тоже изображён триптих и так далее).
А вот пример посвежее — литография «Рисующие руки» нидерландского художника XX века Маурица Эшера:
Чтобы увидеть рекурсию, необязательно идти в картинную галерею — просто посмотрите на герб России. Двуглавый орёл держит в правой лапе скипетр, который увенчан двуглавым орлом, а тот тоже держит скипетр, который… 🙂 В общем — вот:
Рекурсию можно услышать
В музыке есть композиции, которые тоже можно назвать рекурсивными. Американский физик и писатель Дуглас Хофштадтер в своей книге «Гёдель, Эшер, Бах: эта бесконечная гирлянда» рассказывает о рекурсии, приводя в пример джигу из «Французской сюиты №5» Баха.
В первой её части трижды повторяется мелодический переход из тональности соль мажор в ре минор: мелодия как бы вызывает сама себя, погружаясь всё глубже. А во второй части, наоборот, трижды поднимается от ре к соль.
Программисту это может напомнить вычисление факториала числа 3: функция трижды вызывает саму себя, затем трижды возвращается с промежуточными результатами вычислений, а затем — с итоговым.
В лингвистике рекурсией называют способность языка порождать вложенные предложения и конструкции. Например, предложение «Саша читает статью про рекурсию» можно достроить до «Лена смотрит, как Саша читает статью про рекурсию». А его, в свою очередь, превратить в «Ленин друг Петя не одобряет, что Лена смотрит, как Саша читает статью про рекурсию».
Принято считать, что рекурсия свойственна любому человеческому языку (сомнения пока есть только насчёт языка пираха, на котором разговаривают в бразильской части бассейна Амазонки), а распознавать и понимать её — едва ли не врождённая способность людей.
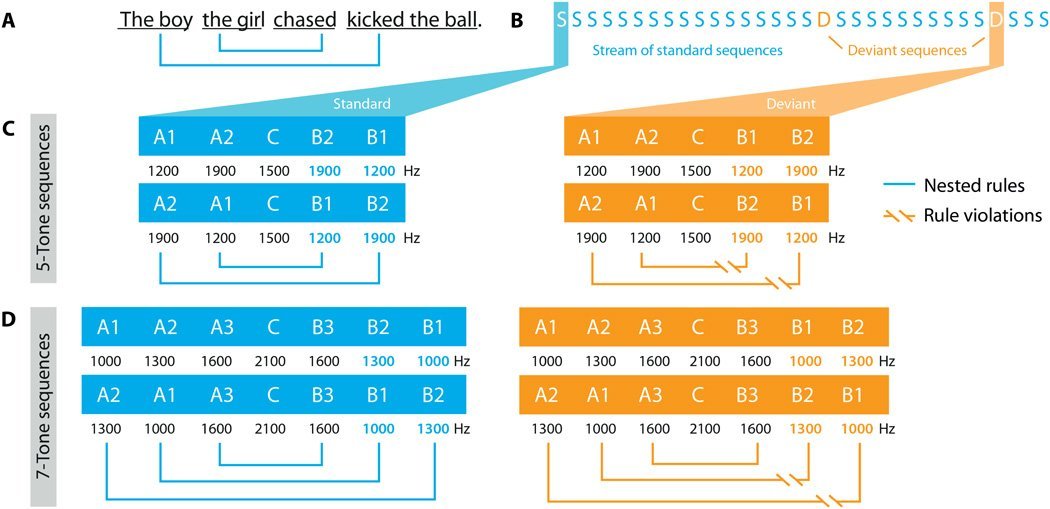
Чтобы доказать это, немецкие учёные даже ставили эксперименты на пятимесячных младенцах. Они измеряли активность головного мозга с помощью ЭЭГ — и сравнивали реакцию малышей на вложенные языковые конструкции, правильные и неправильные. Так как дети были настолько малы, что речь ещё не понимали, вместо слов им проигрывали последовательности звуков разной частоты. Причём частоты звука для связанных слов во вложенных конструкциях совпадали.
В предложении «Мальчик, за которым гналась девочка, пнул мяч» две связанные конструкции: 1) «мальчик пнул» и 2) «девочка гналась». Их обозначили звуками частотой 1900 и 1200 Герц и разделили коротким звуком в 1500 Герц. Слева — корректные, а справа — некорректные языковые паттерны. Кроме пятитоновых, проигрывались и семитоновые вложенные последовательности.
Научные подробности ищите в оригинальной публикации. Нам важнее выводы: эксперименты показали, что даже мозгу младенцев неправильные конструкции определённо не понравились.
Конечно, выборка (38 участников) слишком мала, чтобы распространять результаты на всё человечество, но теория интересная.
Рекурсивные алгоритмы легко смоделировать с помощью подручных средств
Возьмите, например, матрёшку. Все вложенные в неё куклы подобны кукле-шкатулке, кроме наименьшей, которая представляет собой базовый случай. То есть матрёшка — твёрдое воплощение рекурсии.
А если задаться целью поставить синюю точку на самой маленькой кукле, то можно буквально на пальцах реализовать рекурсивный алгоритм:
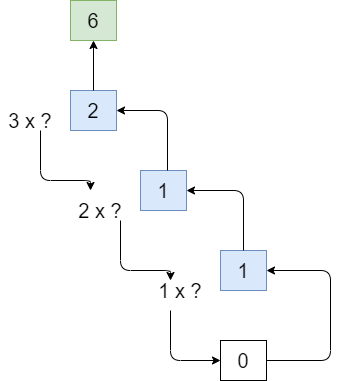
А вот алгоритм, для исполнения которого не нужны дополнительные предметы. Представьте, что вы сидите в последнем ряду длинного зала и хотите узнать, сколько всего в нём рядов. Конечно, можно встать и пересчитать их, но вам лень, а ещё вы уже знаете про рекурсию.
Так что вы спрашиваете соседа спереди, сколько перед ним рядов. Если он называет какое-то число, вы прибавляете к нему ещё два (один ряд — для соседа и один — тот, в котором сами сидите) и получаете ответ, а иначе — предлагаете этому самому соседу применить ваш гениальный алгоритм уже к его соседу спереди.
Если все участники процесса будут настроены доброжелательно, то в итоге очередь отвечать дойдёт до первого ряда и вам обратно по цепочке вернут результат — полученный с помощью рекурсивного алгоритма, между прочим. То есть:
И минутка предметного юмора
— Помнишь, Антоха желание проиграл? Так вот, я ему загадал, чтобы он два дня на все предметы, с которыми что-то сделал, клеил стикер с названием этого действия.
— И что, он на каждый новый стикер клеил другой с надписью «наклеил»?
Подытожим
Рекурсивные предметы и явления окружают нас повсюду. Рекурсию можно увидеть, услышать, потрогать руками. Рекурсия — это просто. Чтобы понять её, не обязательно разбираться с фракталами или фугами Баха. Объяснить рекурсию можно даже пятилетнему ребёнку. Просто прочтите ему стишок Андрея Усачёва:
Шёл по улице жучок
На груди блестел значок,
Нарисован был жучок,
И на нём висел значок,
Был ещё один жучок…
Что глядел я целый час
Был ли у жучка значок?
Был ли на значке жучок?
обложка: Валентина Палатурян для Skillbox
Рекурсия сознания — ловушка мышления и барьер прогрессу. Исторический очерк
С момента появления языка как второй сигнальной системы — инструмента для мышления и общения, человечество получило критическое преимущество перед всеми другими живыми существами, поведение которых управляется системами первого уровня и поэтому принципиально ограничено в уровнях абстрагирования.
Но, давая человеку инструмент огромной силы, язык и абстрактное мышления в то же время создают ограничения и ловушки, ведущие к проблемам, конфликтам и деструктивному поведению. Чем человечество последние 5000 лет в основном и занимается. (Может и 500 000, но нет письменных свидетельств).
Большинство войн, конфликтов, ссор и убийств происходят или оправдываются идейнымы, идеологическими, религиозными, политическими и другим абстрактными причинами, лежащими в сфере идей и информации, а не материального мира. И прежде чем война, конфликт, ссора приводит к реальным действиям, ей всегда предшествует этап намерения, замысла, подготовки, планирования, нагнетания, организации, проходящий на уровне слов и информации.
Источник и инструмент всех войн, убийств, дискриминации, инквизиции, угнетения — язык.
Но он же — инструмент науки, культуры, прогресса, развития, цивилизации.
И виноват в проблемах не инструмент, а незрелое мышление, сознание и культура тех, кто его использует.
Еще с античных времен лучшие умы это понимали и пытались исправить.
Наибольший вклад в развитие цивилизации внес, конечно, Аристотель. Разработка формальной логики дала хоть и простой, но все-же общепризнанный и легко применимый инструмент разрешения споров и поиска истины. По сути, это создало основу, фундамент всей Западной цивилизации.
Хотя до сих пор формальную логику понимает и умеет пользоваться, по разным оценкам, не более 1-10% населения планеты.
И уже в те времена философы и мыслители, используя этот инструмент, натолкнулись на ловушку рекурсии, лежащую в основе значительной части парадоксов, апорий и логических противоречий.
Парадокс лжеца, апории Зенона, множество других парадоксов — в основе всех одна и та же мыслительная ошибка. Считать, что высказывание, направленное само на себя, ничем не отличается от высказываний, имеющих другое основание.
«Это высказывание написано на русском языке», «Это высказывание истинное» — рекурсивные высказывания без парадокса.
«Это высказывание ложное» — пример парадоксальной рекурсии.
Но выхода так и не нашли.
Философы средневековья и Возрождения потратили тысячи часов на решения подобных и еще более схоластических вопросов, но единственным продуктом были все более и более абстрактные теории, в которых авторы избретали новые названия для старых категорий и все больше в них запутывались.
Как ехидно заметил Пуанкаре,
«…все, что ученый на самом деле создает — это язык, которым он это возвещает.»
Выходы из логического тупика начали находить только по мере развития естественных и точных наук где-то к началу XX века. Нашлись они, как и можно было ожидать, представителями самой формальной и точной науки — математики.
Б. Рассел в своих «Основаниях математики» (1903) показал, что класс не может включать сам себя в виде элемента класса, а тип не может быть сам себе подтипом. Аналогично множество, включающее само себя в качестве подмножества, обладает особыми свойствами и не может рассматриваться в ряду обычных множеств, не приводя к логическим ошибкам указанного типа.
Наиболее полно и красиво разобрался с этой проблемой Курт Гёдель, опубликовавший в 1931 году свои знаменитые теоремы о неполноте:
«Любая формальная система аксиом содержит неразрешенные предположения»
«Логическая полнота (или неполнота) любой системы аксиом не может быть доказана в рамках этой системы. Для ее доказательства или опровержения требуются дополнительные аксиомы (усиление системы)».
Доказательство этой вроде бы простой истины, с которой философы не могли справиться тысячелетиями, не прошло даром для ученого — в этой борьбе он подорвал свой разум, поймал серьезную паранойю и умер от голода и истощения, всеми забытый и оставленный.
Так что будьте осторожны с рекурсией, это отражение отражений, из которого можно и не вернуться!
Работы Гёделя оказали серьезное влияние на все точные науки, не только математику.
«…невозможно решить проблему на том же уровне, на котором она возникла. Нужно стать выше этой проблемы, поднявшись на следующий уровень».
По сути, это та же теорема о неполноте, выраженная в более абстрактной форме.
Не обошли вниманием эту тему и отечественные исследователи.
«…действительность, понять которую ставит своей задачей ум, эта действительность является в значительной степени скрытой от него. Она, как говорится, спрятана за семью замками. Между действительностью и умом стоит и должен стоять целый ряд сигналов, которые совершенно заслоняют эту действительность.»
«…Что такое наши слова, которыми мы описываем факты, как не новые сигналы, которые могут, в свою очередь, затемнить, исказить истину.»
«…словесная передача этим другим обстановки всего его дела не соответствует, не воспроизводит точно и полно действительности.»
«…когда вы начнете оперировать с теми словесными сигналами ― этикетками, которые вы поставили на место фактов, ― то здесь фальсификация действительности может достигать огромнейших размеров.»
Это описание тех же уровней абстрагирования, и принципов отношения реальности, языка и сознания, что показаны А. Коржибским на его Структурном Дифференциале в книге «Science and Sanity» в 1933 году, и даже почти теми же самыми словами.
Но, благодаря картинкам и материальной модели, идеи Коржибского все-таки поняли в тот момент несколько человек, (как, впрочем, и Эйнштейна сразу после публикации Теории Относительности) и в результате этого появились и НЛП, и Дианетика с Сайентологией, и некоторые направления позитивной психологии, маркетинга, рекламы, политтехнологий, пропаганды и других инструментов работы с сознанием. К сожалению, на первоисточник авторы этих разработок предпочитают не ссылаться, чтобы «не палить тему».
Но, по крайней мере, идея «Карта — не территория» вышла за рамки научных статей и стала достоянием широкого круга людей и достаточно общепринятым фактом.
А И. Павлов опередил эпоху, и в то непростое время, его глубоко не понял, наверное, вообще никто.
И даже сейчас, через почти 100 лет после этих исследований, публикаций и выступлений, контролировать свое абстрагирование, отслеживать уровни, избегать рекурсии и не попадать в уровневые ловушки умеет не так много людей, на порядки меньше, чем владеют формальной логикой.
Хорошо, что на этом ресурсе собираются люди, близкие к ИТ и программированию, которых с первых шагов в профессии обучают логике, структуре и строгости мышления и которые знают, что программа не должна вызывать сама себя в качестве подпрограммы, массив не может включать сам себя в качестве элемента массива, а переменная не может принимать в качестве значения сама себя.
Но то, что для программистов самоочевидно, совсем не так в других областях науки и деятельности.
Миллионы людей продолжают пытаться выучить язык с помощью языкового описания языка (грамматики), не замечая, что они попадают в логическую ловушку рекурсии без шанса выбраться оттуда.
Когда вы не знаете, как построить предложение на другом языке, чтобы выразить нужную вам мысль, вы сказать этого не можете.
Но когда вы выучили правило и знаете, как построить это предложение, вы все равно сказать это не сможете.
Потому что та зона мозга, которая должна управлять этим действием, занята мыслями о том, как это сделать (правилами).
Рекурсия в чистом виде.
Но этого почти никто не замечает, кроме психологов-физиологов, которые давно используют такой механизм блокировки речи для исследований языка и мышления.
Психолингвист и методист Стивен Крашен сформулировал эту идею в виде «Гипотезы грамматического монитора». Он утверждает, что грамматика не может служить инструментом для порождения устной речи, а только как монитор для последующего контроля и коррекции. Но, исходя из фактов, полученных другими науками, это никакая не гипотеза, а аксиома, следующая из законов логики, математики, психологии, физиологии. И только фрагментация и сегментация наук и все более узкая специализация ученых не позволяет это заметить.
Аналогичные проблемы с бесконтрольным абстрагированием и злоупотреблением рекурсией можно найти в сфере психологии, когда начинают исследовать мышление с помощью мышления, в методологии, когда пытаются управлять управлением с помощью управления, в философии, которая множит абстрактные сущности без всякого страха перед Оккамом, и во многих других сферах человеческой деятельности.
И задача технарей, айтишников, представителей точных наук — помочь выбраться из рекурсивной ловушки, дать инструменты структурирования мышления, научить избегать рекурсии и совместно с гуманитариями разработать новые продукты и инструменты, решающие насущные задачи и лишенные рекурсивных замыканий.
Одним из таких инструментов может быть Структурно-Визуальный метод, разработанный автором этой статьи. Он предлагает для структурирования знаний в некоторой предметной области использовать визуальное представление структуры с использованием цвета для кодирования ограниченного количества смыслов самого верхнего уровня абстракции.
С помощью этого метода были получены некоторые интересные схемы и модели для разных предметных областей — ИТ, управления, психологии, лингвистики, педагогики, изучения иностранных языков, а их практическое применение оказалось довольно результативным и перспективным.
Но об этом в следующих статьях, если это будет интересно читателям Хабра.
Успехов вам в любой деятельности и осознанного абстрагирования!
— алгоритмы, последовательно приближающиеся к заданной цели;
— алгоритмы, в которых поиск решения сводится к формулировке одной или нескольких задач меньшей размерности;
— алгоритмы, соблюдающие установленные для них соотношения (свойства, «законы», инварианты);
Соответственно, меняется и технология их разработки: основной задачей является – направить алгоритм «в нужное русло», заставить двигаться его в нужном направлении, соблюсти «правила игры», правильно свести задачу к аналогичной. Очевидность и наблюдаемость здесь уступают место логической непротиворечивости и доказательности соблюдения программой заданных свойств.
Рекурсивным называется способ построения объекта (понятия, системы, описание действия), в котором определение объекта включает аналогичные объекты (понятие, систему, действие) в виде составных частей.
Рекурсия в жизни, литературе, искусстве
Примеры рекурсии можно встретить в литературе, искусстве, фольклоре.
«У попа была собака, он ее любил.
Камнем придавил, и на камне написал:
«Я оглянулся посмотреть,
не оглянулась ли она,
чтоб посмотреть, не оглянулся ли я. »

Все образные примеры рекурсии подмечают главное ее свойство: некоторая часть системы воспроизводит самое себя. Здесь же отмечается особенность такого подхода: рекурсия не свойственна обыденному восприятию, безусловная рекурсия бесконечна и бессмысленна. Ограниченная рекурсия с определенным количеством уровней – парадоксальна и опасна. Например, рефлексия (от лат. reflexio – обращение назад) – самопознание, самонаблюдение, образное представление самого себя в третьем лице (см., например, «Поединок» А.Куприна).
Примеры рекурсии можно обнаружить математике. Например, рекуррентные соотношения определяют (вычисляют) некоторый элемент последовательности через несколько предыдущих.
В программировании таких примеров еще больше :
— определение любого конкретного оператора (условный, цикл, блок) в качестве составных частей включает произвольный оператор;
Рекурсивные алгоритмы и функции и их свойства
//—— Циклический алгоритм вычисления факториала
for (int s=1; n!=0; n—) s *=n;
//—— Рекурсивный алгоритм вычисления факториала
Приведенный пример не демонстрирует каких-то особенных преимуществ линейной рекурсии. Тем не менее, линейная рекурсия элегантно смотрится на линейных структурах данных – односвязных списках.
//— Включение в односвязный с сохранением порядка – циклическая программа
void InsSort(list *&ph, int v)
// перед переходом к следующему указатель на текущий
// запоминается как указатель на предыдущий
for ( p=ph,pr=NULL; p!=NULL && v>p->val; pr=p,p=p->next);
if ( pr == NULL ) // включение перед первым
else // иначе после предыдущего
//— Рекурсивное включение в односвязный список с сохранением порядка
void InsSort(list *&ph, int v)<
list * pp = new list ; // меньше следующего
Особенность включения в односвязный список – указатель на новый элемент должен быть помещен в предыдущий элемент списка, указатель на который программа должна «помнить». Рекурсия позволяет использовать ссылку на указатель для любого элемента списка.
… if () F 1(); // Не более 2 рекурсивных вызовов
for ( int i =0; i m ; I ++) F 2(); // Рекурсивный вызов в цикле
Все приведенные выше литературно-художественные примеры имеют отношение к линейной рекурсии. Для ветвящейся рекурсии есть только одна физическая аналогия – цепная реакция: каждый рекурсивный вызов порождает n себе подобных. В структурах данных аналогичная «конструкция» называется деревом.
void main() void F() void F() void F()
На самом деле этот эффект воспроизводится в компьютере. Однако копируется при этом не весь текст функции (не вся функция), а только ее части, связанные с локальными данными (формальные, фактические параметры, локальные переменные и точка возврата). Алгоритмическая часть (операторы, выражения) рекурсивной функции и глобальные переменные не меняются, поэтому они присутствуют в памяти компьютера в единственном экземпляре.
— в стеке резервируется место для формальных параметров, в которые записываются значения фактических параметров. Обычно это производится в порядке, обратном их следованию в списке;
— в начале тела функции в стеке резервируется место для локальных (автоматических) переменных.
Перечисленные переменные образуют группу (фрейм стека). Стек «помнит историю» рекурсивных вызовов в виде последовательности (цепочки) таких фреймов. Программа в каждый конкретный момент работает с последним вызовом и с последним фреймом. При завершении рекурсии программа возвращается к предыдущей версии рекурсивной функции и к предыдущему фрейму в стеке.
Рекуррентные соотношения
// Вычисление чисел Фибоначчи итерационным методом
// F 2 – «позавчерашнее» значение ряда
// F 1 – «вчерашнее» значение ряда
// F 0 – «сегодняшнее» значение ряда
F 2= F 1, F 1= F 0; // при переходе к следующему шагу текущий становится
В данной последовательности нет необходимости использовать массив, поскольку вычисляемые элементы последовательности находятся рядом, иначе потребуется более «глубокое» запоминание. Это же соотношение, вычисляемое наоборот, последующий – через предыдущие, напрямую реализуется рекурсивной функцией.
// Рекурсивное вычисление чисел Фибоначчи
Трудоемкость рекурсивных алгоритмов
Изменение размерности задачи
не каждом шаге рекурсии возникает N задач размерности, меньшей на 1, на каждом шаге число выполняемых операций пропорционально размерности задачи.
с каждым шагом рекурсии размерность задачи уменьшается на 1, на каждом шаге число выполняемых операций пропорционально размерности задачи.
с каждым шагом рекурсии размерность задачи уменьшается в два раза при выполнении единственной на этом шаге операции
с каждым шагом рекурсии размерность задачи уменьшается в два раза, число операций на каждом шаге пропорционально размерности задачи. Общая трудоемкость
с каждым шагом рекурсии задача разбивается на две, размерность которых в два раза меньше исходной, число операций на каждом шаге пропорционально размерности задачи
с каждым шагом рекурсии задача разбивается на две, размерность которых в два раза меньше исходной, при выполнении единственной на этом шаге операции.