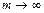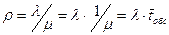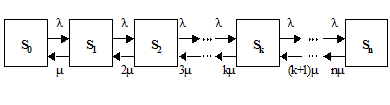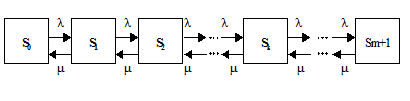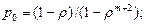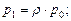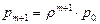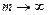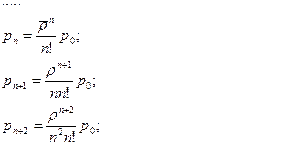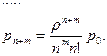теория массового обслуживания примеры в жизни
Теория массового обслуживания примеры в жизни
Большинство систем, с которыми человек имеет дело, являются стохастическими. Попытка их математического описания с помощью детерминистических моделей приводит к огрублению истинного положения вещей. При решении задач анализа и проектирования таких систем приходится считаться с положением вещей, когда случайность является определяющей для процессов, протекающих в системах. При этом пренебрежение случайностью, попытка “втиснуть” решение перечисленных задач в детерминистические рамки приводит к искажению, к ошибкам в выводах и практических рекомендациях.
Первые задачи теории систем массового обслуживания (ТСМО) были рассмотрены сотрудником Копенгагенской телефонной компании, датским ученым А.К. Эрлангом (1878- 1929г) в период между 1908 и 1922гг. Эти задачи были вызваны к жизни стремлением упорядочить работу телефонной сети и разработать методы, позволяющие заранее повысить качество обслуживания потребителей в зависимости от числа используемых устройств. Оказалось, что ситуации, возникающие на телефонных станциях, являются типичными не только для телефонной связи. Работа аэродромов, морских и речных портов, магазинов, терминальных классов, электронных вычислительных комплексов, радиолокационных станций и т.д. может быть описана в рамках ТСМО.
1.2. Примеры систем массового обслуживания. Анализ задач ТСМО.
Пример 1. Телефонная связь времен Эрланга представляла из себя телефонную станцию, связанную с большим числом абонентов. Телефонистки станции по мере поступления вызовов соединяли телефонные номера между собой.
Задача: Какое количество телефонисток (при условии их полной занятости) должно работать на станции для того, чтобы потери требований были минимальными.
Пример 2. Система скорой помощи некоего городского района представляет собой пункт (который принимает требования на выполнение), некоторое количество автомашин скорой помощи и несколько врачебных бригад.
Задача: Определить количество врачей, вспомогательного персонала, автомашин, для того чтобы время ожидания вызова было для больных оптимальным при условии минимизации затрат на эксплуатацию системы и максимизации качества обслуживания.
Пример 3. Важной задачей является организация морских и речных перевозок грузов. При этом особое значение имеют оптимальное использование судов и портовых сооружений.
Задача: Обеспечить определенный объем перевозок при минимальных расходах. При этом сократить простои судов при погрузочно-разгрузочных работах.
Пример 4. Система обработки информации содержит мультиплексный канал и несколько ЭВМ. Сигналы от датчиков поступают на мультиплексный канал, где буферизуются и предварительно обрабатываются. Затем поступают в ту ЭВМ, где очередь минимальна.
Задача: Обеспечить ускорение обработки сигналов при заданной суммарной длине очереди.
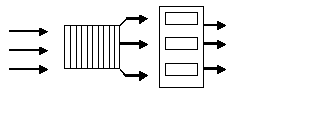
Пример 5. На рис 1.1. изображена структурная схема типичной системы массового обслуживания – ремонтного предприятия (например, по ремонту ПЭВМ). Порядок ее работы ясен из схемы и не требует разъяснений.
Нетрудно привести множество других примеров из самых различных областей деятельности.
Характерным для таких задач является:
2)проблема бича нашего времени – очередей: судов перед шлюзами, машин перед прилавками, задач на входе процессоров вычислительного комплекса и т.д.
А.К. Эрланг обратил внимание на то, что СМО могут быть разделены на два типа, а именно: на системы с ожиданием и системы с потерями. В первом случае – заявка, поступившая на вход системы “ждет” очереди на выполнение, во втором – она из-за занятости канала обслуживания получает отказ и теряется для СМО.
В дальнейшем мы увидим, что к классическим задачам Эрланга прибавляются новые задачи:
Реальные системы, с которыми приходится иметь дело на практике, как правило, очень сложны и включают в себя ряд этапов (стадий) обслуживания (рис 1.1.). Причем на каждом этапе может существовать вероятность отказа в выполнении или существует ситуация приоритетного обслуживания по отношению к другим требованиям. При этом отдельные звенья обслуживания могут прекратить свою работу (для ремонта, подналадки и т.д.) или могут быть подключены дополнительные средства. Могут быть такие обстоятельства, когда требования, получившие отказ, вновь возвращаются в систему (подобное может происходить в информационных системах).
1.3. Понятия, определения, терминология.
Все СМО имеют вполне определенную структуру, изображенную на рис 1.2
1.4. Классификация СМО.
1.4.1. По характеру источника требований различают СМО с конечным и бесконечным количеством требований на входе.
В первом случае в системе циркулирует конечное, обычно постоянное количество требований, которые после завершения обслуживания возвращаются в источник.
Во втором случае источник генерирует бесконечное число требований.
Пример 1. Цех с постоянным количеством станков или определенное количество ПЭВМ в терминальном классе, требующих постоянного профилактического осмотра и ремонта.
Пример 2. Сеть Internet с бесконечным требованием на входе, любой магазин, парикмахерская и т.д.
Первый вид СМО называют замкнутой, второй – разомкнутой.
1.4.2. По дисциплине обслуживания:
В первом случае заявка получает отказ, когда канал занят. Во втором случае – ставится в очередь и ждет освобождения канала. В третьем случае вводится ограничения на длительность ожидания.
1.4.4. По количеству единиц обслуживания:
1.4.6. По свойствам каналов: на однородные, когда каналы имеют одинаковую характеристику и неоднородные в противном случае.
Примеры систем массового обслуживания



| СМО | Заявки | Каналы |
| Автобусный маршрут и перевозка пассажиров | Пассажиры | Автобусы |
| Производственный конвейер по обработке деталей | Детали, узлы | Станки, склады |
| Автосамосвалы и экскаваторы при проведении открытых горных работ | Автосамосвалы | Экскаваторы |
| Чиновники, ведущие прием граждан | Граждане | Чиновники |
| Задачи, решаемые процессором компьютера | Задачи | Процессор компьютера |
В составе СМО можно выделить следующие основные части (рис.3.1):
4. Выходящий поток заявок, т.е. заявок, которые обслужены, или тех, которым в обслуживании было отказано.
 |
В зависимости от емкости накопителя различают СМО с конечной и бесконечной очередью.
Все системы массового обслуживания классифицируются по правилам их работы следующим образом:
1. Системы с отказами, в которых заявка, поступившая в момент, когда все каналы заняты, покидает СМО;
2. Системы с очередью (с ожиданием), в которых заявка, поступившая в момент, когда все каналы заняты, становится в очередь до освобождения одного из каналов; системы с очередью делятся на системы с ограниченным и системы с неограниченным ожиданием.
Порядок, в котором формируется очередь на обслуживание, называется дисциплиной очереди. Различают следующие дисциплины обслуживания: бесприоритетные и приоритетные.
Важнейшие бесприоритетные дисциплины обслуживания:
· FIFO (First In, First Out — первым пришел, первым ушел): если заявка первой пришла в очередь, то она первой уйдет на обслуживание;
· LIFO (Last In, First Out — последним пришел, первым ушел): если заявка последней пришла в очередь, то она первой уйдет на обслуживание (пример — патроны в рожке автомата);
· SF (Short Forward — короткие вперед): в первую очередь обслуживаются те заявки из очереди, которые имеют меньшее время обслуживания.
· RANDOM (случайный выбор).
При приоритетном обслуживании заявке задается некоторый параметр, который определяет его приоритет. Этот параметр может задаваться в числовом виде (статический приоритет) или в виде функции, которая зависит от времени пребывания в системе (динамический приоритет).
В системах с ожиданием накопитель в общем случае может иметь сложную структуру.
Если источник входящего потока заявок расположен вне системы, то СМО называется открытой, а если обслуженная заявка через некоторое время снова возвращается во входящий поток, то СМО называется замкнутой.
Основные показатели функционирования СМО могут быть вычислены в зависимости от типа СМО
Поскольку заявки поступают на обслуживание в СМО в случайные моменты времени, имеет смысл говорить о потоке заявок, характеристикой которого служит закон распределения. Обслуживание поступившей заявки продолжается некоторое (тоже случайное) время, что приводит к тому, что в какие-то промежутки времени поступившие заявки либо образуют очередь на обслуживание, либо покидают систему необслуженными, в другие же периоды СМО может работать с недогрузкой.
Анализ зависимости между характером потока заявок, числом каналов, их производительностью и эффективностью обслуживания и есть предмет теории систем массового обслуживания (СМО). Одним из основных математических понятий в теории СМО является понятие потока событий.
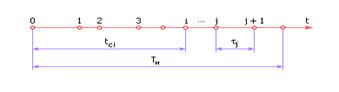
где τj — интервал между событиями (случайная величина);
tсi — момент совершения i-го события (отсчитывается от t = 0);
Рис. 3.2. Пример потока событий
Простейший поток определяется тремя условиями:
1. Стационарностью – среднее число требований в единицу времени постоянно;
2. Отсутствием последействия – число требований, поступающих в некоторый промежуток времени, не зависит от числа требований, поступивших в предыдущем промежутке;
3. Ординарностью – вероятность поступления более одного требования в малый промежуток времени 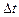
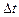

Установлено, что интервал времени между событиями в этом потоке есть случайная величина, распределенная по показательному (по экспоненциальному) закону, плотность которого определяется формулой:
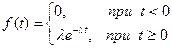
где 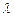
Используя основное свойство математического ожидания случайной величины, приходим к выводу о том, что средний интервал времени между двумя событиями в потоке равен 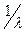
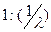
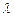
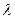
Для непрерывного распределения, зная плотность распределения f(x),можно найти функцию распределения F(x)по формуле
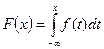
Случайная величина, следующая экспоненциальному распределению, имеет функцию распределения
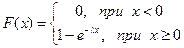
Знание функции плотности и функции распределения позволит вычислить 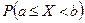
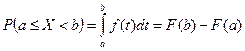
Если 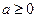
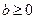
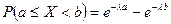
Другой случайной величиной, связанной с простейшим потоком событий является количество событий, происходящих в единицу времени. Эта случайная величина распределена по закону Пуассона. Это распределение является дискретным распределением и описывается формулой
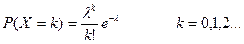
где λ>0– параметр распределения.
Формула (3.6) позволяет вычислить вероятность того, что в течение одной минуты произойдет ровно k событий. Основные описательные статистики для распределения Пуассона, выражаются следующими соотношениями (3.7):
Поскольку математическое ожидание случайной величины M(X) распределенной по закону, равно, 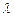
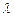
Необходимо отметить, что оба распределения (экспоненциальное и распределение Пуассона), описывающие один и тот же поток событий, содержат один и тот же параметр λ, характеризующий интенсивность потока.
Поэтому при моделировании СМО часто принимают допущение о том, что поток входящих заявок (требований) и поток обслуженных требований являются простейшими.
В данной работе будем полагать, что интенсивность потока входящих заявок равна 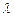
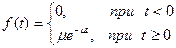
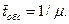
При анализе СМО часто используется характеристика, которая называется приведенной интенсивностью потока требований, равная отношению интенсивности потока входящих заявок к интенсивности обслуживания заявок. Обозначим это отношение через 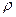
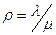
Приведенная интенсивность потока требований характеризует число требований, поступивших в систему за время обслуживания одного. Чтобы показать справедливость этого утверждения, приведем следующие соотношения:
Судить о результатах работы СМО можно по следующим показателям:
· относительная пропускная способность системы;
· абсолютная пропускная способность системы;
· вероятность отказа клиенту в обслуживании;
· вероятность занятости всех каналов;
· среднее количество занятых каналов;
· вероятность простоя каждого канала;
· вероятность простоя всей системы;
· среднее количество заявок, стоящих в очереди;
· среднее время ожидания заявки в очереди;
· среднее время обслуживания заявки;
· среднее время нахождения заявки в системе;
· среднее время занятости каждого канала;
· вероятность занятости каждого из каналов.
Судить о качестве полученной системы нужно по совокупности значений показателей. К числу важнейших показателей относятся: относительная и абсолютная пропускные способности системы. Абсолютная пропускная способность системы 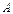
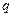
МНОГОКАНАЛЬНАЯ СМО С ОТКАЗАМИ
Если в момент поступления требования нет свободных обслуживающих каналов (т.е. заняты все каналы, так как в системе уже находится n требований), то требование покидает систему не обслуженным. Все состояния системы приведены на рис. 3.4.
Рис. 3.4. Граф состояний для многоканальной СМО с отказами
S0 – все каналы свободны;
S1 – один канал занят, остальные свободны;
S2 – два канала заняты, остальные свободны;
Sk – k каналов занято, остальные (n-k) свободны;
Sn – все n каналов заняты.
Для расчета многоканальных систем массового обслуживания с отказами воспользуемся формулами Эрланга. Входящий поток требований подчиняется пуассоновскому закону с интенсивностью l, а время обслуживания – показательному с интенсивностью m.
Вероятность наличия в системе k требований:
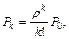
где 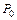
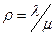
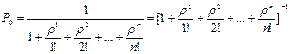
Вероятность потери требования (отказа) соответствует вероятности наличия в системе n требований, когда все n каналов заняты
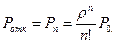
Относительная пропускная способность
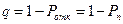
Абсолютная пропускная способность
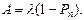
Среднее количество заявок, находящихся в системе, соответствует среднему числу занятых каналов и определяется по формуле
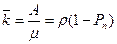
ОДНОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ
Граф состояний одноканальной СМО с ожиданием приводится на рис. 3.5.
Рис. 3.5. Граф состояний для одноканальной СМО с ожиданием
S0 – все каналы свободны;
S1 – один канал занят, очереди нет;
S2 –канал занят, одна заявка в очереди;
Sk – канал занят, k-1 заявка в очереди;
Sm+1 – канал занят, m заявок в очереди.
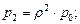
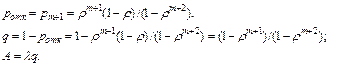
Среднее число заявок, находящихся в очереди
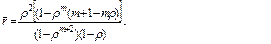
Среднее число заявок, находящихся в системе (как стоящих в очереди, так и находящихся на обслуживании)

Среднее время пребывания заявки в очереди и в системе соответственно
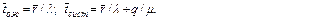
ОДНОКАНАЛЬНАЯ СМО С НЕОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ.

При отсутствии ограничений по длине очереди каждая заявка, пришедшая в систему будет обслужена, поэтому 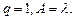
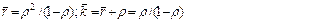
Среднее время пребывания заявки в очереди и в системе
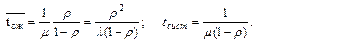
МНОГОКАНАЛЬНАЯ СМО С ОЖИДАНИЕМ
Рассмотрим n-канальную СМО с ожиданием (интенсивность потока заявок l; интенсивность обслуживания m, число мест в очереди m). Состояния системы (рис. 3.4) следующие:
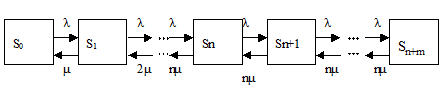
S1 – занят один канал, остальные свободны;
Sn+1 – занято n каналов, одна заявка в очереди;
Sn+m – занято n каналов, m заявок в очереди.
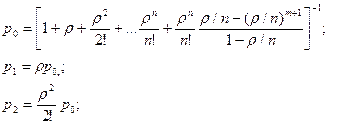
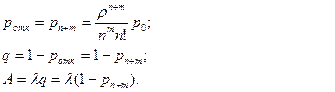
Среднее число занятых каналов и заявок в очереди соответственно
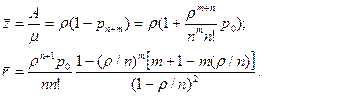
Обозначив 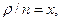
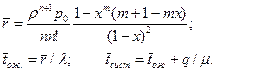
МНОГОКАНАЛЬНАЯ СМО С НЕОГРАНИЧЕННОЙ ОЧЕРЕДЬЮ
Снимем ограничение на длину очереди в задаче предыдущего раздела.
Вероятности состояний получим предельным переходом (при