Во что превратилась бы через 4 года сумма в 100 рублей
Сложные проценты в ЕГЭ. 10–11-е классы
Разделы: Математика
«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам».
Д. Пойа.
Введение.
1. При решении задач на проценты используются основные формулы:
1% числа а равен
а.
р% от числа а равно 
Если известно, что некоторое число а составляет р% от х, то х можно найти из пропорции
х − 100%,
откуда х= а
Пусть имеются числа a, b, причем а 4 + х∙1,5 3 + х∙1,5 2 +х∙1,5
Для этого вынесем х за скобку и вычислим сумму геометрической прогрессии, в которой b = 1,5 и q = 1,5.
Известно, что размер вклада увеличился по сравнению с первоначальным на 725%.
Это значит, что он стал составлять 825% от начального, т.е. увеличился в 8,25 раз.
Сумма всех слагаемых последнего столбика в 8,25 раз больше, чем 3900 тыс.руб.
Задачи на проценты из номера 17 егэ по математике
Задачи на проценты
1. При решении задач на проценты используются основные формулы:
1% числа а равен 
р% от числа а равно 
Если известно, что некоторое число а составляет р% от х, то х можно найти из пропорции
откуда х= а 
Пусть имеются числа a, b, причем а
Число b больше числа а на 
Число а меньше числа b на 
2. Формула сложных процентов.
Если на вклад положена сумма а денежных единиц, банк начисляет р% годовых, то через n лет сумма на вкладе составит
a 
3. Задачи на проценты.
Задача 1. Умных людей на 45 % меньше, чем красивых, 36% умных обладают красивой внешностью. Каков процент умных людей среди красивых?
Решение: пусть х − количество красивых людей, тогда количество умных людей:
Среди умных 36% составляют красивые люди, следовательно, количество умных и одновременно красивых людей:
Учащиеся с интересом решают текстовые задачи на проценты, которые ближе к реальной жизни. Особый «прикол» представляет собой подача задач не из задачника, а прямо с газетной полосы. Тут уж не возникает мыслей о ненужности математики. А «процентная журналистика» в связи с разразившимся экономическим кризисом на страницах газет буквально процветает.
Задача 2. Цены на путевки уже подросли: например, туры во Францию − на 20%. Можно ли сказать, на сколько процентов раньше тур во Францию был дешевле?
Решение: пусть х − старая цена, а n − новая цена.
1) Составим первую пропорцию:
2) Составим вторую пропорцию:
Решив уравнение, получим: а ≈17%.
3. Четыре одинаковые рубашки дешевле куртки на 4%. На сколько процентов шесть таких же рубашек дороже куртки?
Четыре рубашки – это 96% от стоимости куртки, тогда одна рубашка – это 24% от стоимости куртки, а шесть таких рубашек – 24 ⋅ 6=144%.
Значит, шесть рубашек дороже куртки на 44%.
4. Три одинаковые рубашки дешевле куртки на 10%. На сколько процентов четыре такие же рубашки дороже куртки?
Три рубашки – это 90% от стоимости куртки, тогда одна рубашка – это 30% от стоимости куртки, а четыре рубашки – 30 ∗ 4=120%.
5. Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вчетверо, общий доход семьи вырос бы на 165%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 1%.
Сколько процентов от общего дохода семьи составляет зарплата жены?
А т. к. при уменьшении стипендии дочери доход семьи сократился бы на 1%, то
Тогда доход жены (в %) равен: 100−(55+2)=43.
6. Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 51%. Если бы стипендия дочери уменьшилась вдвое, общий доход семьи сократился бы на 1%.
Сколько процентов от общего дохода семьи составляет зарплата жены?
А т. к. при уменьшении стипендии дочери доход семьи сократился бы на 1%, то
Тогда доход жены (в %) равен: 100−(51+2)=47.
4. Использование формулы сложных процентов.
Задача 7. В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник.
На сколько процентов подорожали акции компании в понедельник?
8. На банковский счет было положено 10 тыс. руб. После того, как деньги пролежали один год, со счета сняли 1 тыс. руб. Еще через год на счету стало 11 тыс. руб. Определите, какой процент годовых начисляет банк.
Решение: пусть банк начисляет р% годовых.
1) Сумма в 10000 рублей, положенная на банковский под р% годовых, через год возрастет до величины
10000+
2) Когда со счета снимут 1000 руб., там останется 9000+100р руб.
3) Еще через год последняя величина за счет начисления процентов возрастет до величины
9000+100р+
По условию эта величина равна 11000:
Решив это уравнение получим: 

Решение: от суммы вклада ситуация не изменится. Положим в банк 4 рубля (делится на 4 ). Через год сумма на счету увеличится ровно в p раз и станет равной (4p) рублей.
Поделим её на 4 части, унесём домой (p) рублей, оставим в банке (3p) рублей.
Таким образом, найден второй повышающий коэффициент k банка.
Интересно, что произведение обоих коэффициентов равно 1,92 :
Из условия следует, что второй коэффициент на 0,4 больше первого.
Избавившись от запятых, сделаем замену t = 10р :
Из такого уравнения получить 12 совсем просто.
Было 100%, стало 160%. Новый процент годовых равен 160%-100% = 60%.
Решение: пусть х рублей – вкладчик ежегодно добавлял ко вкладу.
Посчитаем, какой доход принесли все четыре добавки.
х∙1,5 4 + х∙1,5 3 + х∙1,5 2 +х∙1,5
Это значит, что он стал составлять 825% от начального, т.е. увеличился в 8,25 раз.
Сумма всех слагаемых последнего столбика в 8,25 раз больше, чем 3900 тыс.руб.
Сложный процент
Сложным процентом принято называть эффект, когда проценты прибыли прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли.
Формула сложного процента — это формула, по которой рассчитывается итоговая сумма с учётом капитализации (начислении процентов).
Простой расчет сложных процентов
Чтобы лучше усвоить расчет сложных процентов, давайте разберём пример.
Представим, что вы положили 10 000 руб в банк под 10 процентов годовых.
Через год на вашем банковском счету будет лежать сумма SUM = 10000 + 10000*10% = 11 000 руб.
Ваша прибыль — 1000 рублей.
Вы решили оставить 11 000 руб на второй год в банке под те же 10 процентов.
Через 2 года в банке накопится 11000 + 11000*10% = 12 100 руб.
Прибыль за первый год (1000 рублей) прибавилась к основной сумме (10000р) и на второй год уже сама генерировала новую прибыль. Тогда на 3-й год прибыль за 2-й год прибавится к основной сумме и будет сама генерировать новую прибыль. И так далее.
Этот эффект и получил название сложный процент.
Когда вся прибыль прибавляется к основной сумме и в дальнейшем уже сама производит новую прибыль.
Формула сложного процента:
SUM = X * (1 + %) n
где
SUM — конечная сумма;
X — начальная сумма;
% — процентная ставка, процентов годовых /100;
n — количество периодов, лет (месяцев, кварталов).
Расчет сложных процентов: Пример 1.
Вы положили 50 000 руб в банк под 10% годовых на 5 лет. Какая сумма будет у вас через 5 лет? Рассчитаем по формуле сложного процента:
SUM = 50000 * (1 + 10/100) 5 = 80 525, 5 руб.
Сложный процент может использоваться, когда вы открываете срочный вклад в банке. По условиям банковского договора процент может начисляться например ежеквартально, либо ежемесячно.
Расчет сложных процентов: Пример 2.
Рассчитаем, какая будет конечная сумма, если вы положили 10 000 руб на 12 месяцев под 10% годовых с ежемесячным начислением процентов.
SUM = 10000 * (1+10/100/12) 12 = 11047,13 руб.
ПРИБЫЛЬ = 11047,13 — 10000 = 1047,13 руб
Доходность составила (в процентах годовых):
% = 1047,13 / 10000 = 10,47 %
То есть при ежемесячном начислении процентов доходность оказывается больше, чем при начислении процентов один раз за весь период.
Если вы не снимаете прибыль, тогда начинает работать сложный процент.
Формула сложного процента для банковских вкладов
На самом деле формула сложного процента применительно к банковским вкладам несколько сложнее, чем описана выше. Процентная ставка для вклада (%) рассчитывается так:
% = p * d / y
где
p — процентная ставка (процентов годовых / 100) по вкладу,
например, если ставка 10,5%, то p = 10,5 / 100 = 0,105;
d — период (количество дней), по итогам которого происходит капитализация (начисляются проценты),
например, если капитализация ежемесячная, то d = 30 дней
если капитализация раз в 3 месяца, то d = 90 дней;
y — количество дней в календарном году (365 или 366).
То есть можно рассчитывать процентную ставку для различных периодов вклада.
Формула сложного процента для банковских вкладов выглядит так:
При расчете сложных процентов нужно принимать во внимание тот факт, что со временем наращивание денег превращается в лавину. В этом привлекательность сложных процентов. Представьте себе маленький снежный комок размером с кулак, который начал катиться со снежной горы. Пока комок катится, снег налипает на него со всех сторон и к подножию прилетит огромный снежный камень. Также и со сложным процентом. Поначалу прибавка, создаваемая сложным процентом, почти незаметна. Но через какое-то время она показывает себя во всей красе. Наглядно это можно увидеть на примере ниже.
Расчет сложных процентов: Пример 3.
Рассмотрим 2 варианта:
1. Простой процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Всю прибыль вы снимаете.
2. Сложный процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Каждый год проценты прибыли прибавляются к основной сумме.
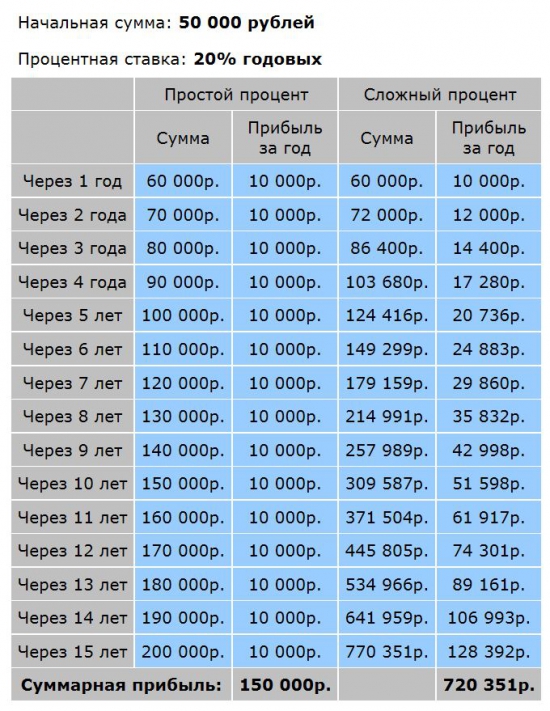  |
Комментарии, как говорится, излишни. Вложения с использованием сложного процента НА ПОРЯДОК выгоднее, чем с простым процентом. Чем больше проценты прибыли, чем дольше срок инвестирования, тем ярче проявляет себя сложный процент.
В случае простого процента график увеличения капитала получается линейный, поскольку вы снимаете прибыль и не даёте ей работать и приносить новую прибыль. В случае сложного процента график получается экспоненциальным, с течением времени кривая увеличения капитала становится всё круче, всё больше стремится вверх. Это происходит оттого, что из года в год прибыль накапливается и создаёт новую прибыль.
На графике ниже показано как вырастет капитал, если вложить 50 000 руб на 15 лет под 10%, 15% и 20%.
 |
Как видите, на длительном промежутке времени очень важным становится то, под какой процент вы инвестируете деньги.
Через 15 лет при 10% годовых 50 тысяч рублей превратятся в 200 тысяч, при 15% — уже в 400 тысяч, а при 20% годовых — в 780 тысяч.
Таким образом, сложный процент является мощным орудием по увеличению капитала на длительных промежутках времени.
Из формулы расчёта сложного процента можно выразить процентную ставку и количество лет (месяцев).
Процентная ставка:
Расчет сложных процентов: Пример 4.
Какая процентная ставка должна быть, чтобы за 10 лет 50 000 рублей превратились в 100 000 рублей?
% = (100000 / 50000) 1/10 — 1 = 0,0718 = 7,18 % годовых
Количество периодов (месяцев, лет):
n = log(1+0,4) (1000000 / 50000) = 8,9 лет
Тогда ее значение А1 после первого увеличения находится по формуле
An=A(1+P/100) n (1)
Это формулы сложных процентов.
Задача №16.
Сбербанк начисляет ежегодно 3% от суммы вклада. Через сколько лет сумма вклада удвоится?
Пусть x – искомое число лет,
А – первоначальная сумма,
2А – удвоенная сумма,
Тогда по формуле (1) получаем:
Ответ: около 23 лет.
Задача №17.
Число 51.2 трижды увеличивали на одно и то же число процентов, а затем трижды уменьшали на то же самое число процентов. В результате получилось число 21.6. На сколько процентов увеличивали, а затем уменьшали это число?
Пусть x – искомое число. Тогда по формуле (2) имеем:
21,6=51,2(1+x/100) 3 (1-x/100) 3 ;
Задача №18.
Вкладчик открыл в банке счет и положил на него S0=150 000руб. сроком на 4 года по ставке 18% в год. Какой будет сумма S4, которую вкладчик получит при закрытии вклада? На сколько рублей вырастет вклад за 4 года? Чему равен коэффициент наращивания?
S0=150 000 рублей, р=18, n=4.
По формуле (1) имеем:
S4=150000(1+18/100) 4 =258000
За 4 года вклад увеличится на 108 000 рублей=258 000руб. – 150 000руб. Коэффициент наращивания равен:
S4/S0 =1, т.е. первоначальный вклад увеличится в 1.72 раза.
Задача №19.
Какую сумму положили в банк под 22% годовых, если через 5 лет вклад достиг величины S5=94500 рублей?
По условию р=22, n=5, S5=94500
Ответ: первоначальная сумма вклада была 34965 рублей.
Задача №20.
Сколько лет лежал в банке вклад 70000 рублей, если по ставке 19.2% годовых процентов он достиг величины 150640 рублей. Чему равен коэффициент наращивания?
По формуле (1) имеем:
Коэффициент наращивания Sn/S0=150640/70000=2,152
Два банка начисляют определенные проценты по вкладам (свои в каждом банке). Причем первый из них начисляет …….лежащую на счет сумму, второй начисляет проценты по вкладу в конце года. Если клиент положит на 2 года 1/3 имеющейся у него суммы денег в первый банк, то его прибыль составит 66% от первоначальной суммы. Если же наоборот, 2/3 исходной суммы денег положит в первый банк, а оставшуюся часть во второй, то через 2 года прибыль составит 76%. Какую бы сумму получил клиент через 2 года, если бы положил на этот срок сумму денег в размере 1000 условных единиц в равных долях в оба банка?
Тема 2. Методологические основы принятия финансовых решений
Цель практикума по данной теме — сформировать навык решения задач на основе дисконтирования и компаундирования, обучить методам оценки доходности и риска, ознакомить с правилами решений в условиях риска и неопределенности.
Методические указания
Приступая к рассмотрению примеров и самостоятельному решению задач, необходимо внимательно прочесть контент по соответствующему вопросу темы. Базовые концепции в данной теме — это концепция денежного потока и концепция временной ценности денег. Важнейшие понятия: простые и сложные проценты, денежный поток, современная (настоящая) и будущая стоимости, внутренняя стоимость, доход, доходность и риск. Эти понятия следует выучить и разобраться в их соотношениях.
В решении задач используются формулы, объяснение которых представлено в контенте. Для облегчения поиска необходимых разъяснений в контенте нумерация формул и обозначения в практикуме такие же, как и в контенте.
2.1. Денежные потоки и методы их оценки
В данном параграфе используются следующие обозначения:
A — одинаковый ежегодный (ежеквартальный, ежемесячный и т. п.) приток/отток денег (выплаты, арендная плата), ден. ед.;

D — доход, дивиденд, ден. ед.;
d — учетная ставка, доходность, %;
F — будущая стоимость (вклада, будущая сумма возвращаемого долга), ден. ед.;
FV — будущая (наращенная) стоимость денежного потока, ден. ед.;

k — количество периодов, лет, месяцев, дней;
m — число начислений в год, разы;
n — срок аренды (выплат, погашения долга, денежного потока), годы, месяцы, дни;
P — настоящая стоимость (вклада, долга), ден. ед.;
PV — настоящая (дисконтированная, приведенная) стоимость денежного потока, ден. ед.;

r — процентная ставка (ставка наращения, ставка дисконтирования), %;

V — внутренняя стоимость.
Задача 2.1.1.
Определить, чему равны учетная и процентная ставки при возрастании стоимости за год с 12 до 15 тыс. р.
Методические указания: использовать формулы (2.1.1), (2.1.2).
Дано:
Решение:
Учетная ставка находится по отношению к будущей стоимости:
Процентная ставка находится по отношению к настоящей (современной) стоимости:
Ответ: Учетная ставка равна 20 %, процентная ставка равна 25 %.
Задача 2.1.2.
Какая сумма будет в банке через 3 года, если вложено 120 тыс. р. под 11 % годовых: а) без капитализации; б) с капитализацией?
Методические указания: использовать формулы (2.1.3), (2.1.5), (2.1.7).
Дано:
Решение:
По схеме простых процентов (без капитализации) наращенная сумма вклада составит:
F = P х (1 + r х n) = 120 х (1 + 0,11 х 3)=159,6 тыс. р.
При условии капитализации дохода используется
схема сложных процентов:
Ответ:
а) без капитализации сумма составит 159,6 тыс. р.
б) с капитализацией сумма составит 164,1 тыс. р.
Задача 2.1.3.
Сколько нужно вложить в банк для получения через 5 лет 400 тыс. р. под 15 % годовых: а) без капитализации; б) с капитализацией?
Методические указания: использовать формулы (2.1.3), (2.1.4), (2.1.5), (2.1.7).
Дано:
Решение:
Из формулы 2.1.5 (схема простых процентов) следует:
Из формулы 2.1.7 (схема сложных процентов) следует:
Задача 2.1.4.
Под какой процент следует вложить 100 тыс. р., чтобы получить 200 тыс. р. через 4 года?
Методические указания: использовать формулы (2.1.5), (2.1.7).
Дано:
Решение:
Поскольку в условии не уточняется, какую схему наращения следует использовать, рассмотрим оба варианта.
По схеме простых процентов наращение осуществляется по формуле 2.1.5, из которой следует:
По схеме сложных процентов наращение осуществляется по формуле 2.1.7, из которой следует:
Ответ: 100 тыс. р. следует вложить: а) без капитализации под 25 % годовых, б) с капитализацией — под 18,9 % годовых.
Задача 2.1.5.
Определить период начисления, за который первоначальный капитал в размере 25 тыс. р. вырастет до 40 тыс. р., если используется простая процентная ставка 20 % годовых.
Методические указания: использовать формулы (2.1.5).
Дано:
Решение:
Период начисления определяется по схеме простых процентов:
Ответ: Период начисления, за который первоначальный капитал увеличится до 40 тыс. р., составит 3 года.
Задача 2.1.6.
Кредит выдается под простую ставку 26 % годовых на 250 дней. Рассчитать сумму, получаемую заемщиком, и сумму процентных денег, если требуется возвратить 40 тыс. р.
Методические указания: использовать формулы (2.1.5), (2.1.6).
Дано:
Решение:
Сумма, получаемая заемщиком, определяется по схеме простых процентов:
Поскольку ставка годовая, срок займа следует выразить в годах:
Ответ: Сумма, получаемая заемщиком, 33 955,8 р., сумма процентных денег 6 044,2 р.
Задача 2.1.7.
Рассчитать учетную ставку, которая обеспечивает получение 9 млн р., если сумма в 10 млн р. выдается в ссуду на полгода.
Методические указания: использовать формулу (2.1.6).
Дано:
Решение:
Учетная ставка определяется по схеме простых процентов:

Ответ: Учетная ставка составляет 20 %.
Задача 2.1.8.
Определить современное значение суммы в 120 тыс. р., которая будет выплачена через 2 года, при использовании сложной учетной ставки 18 % годовых.
Методические указания: использовать формулы (2.1.6), (2.1.7).
Дано:
Решение:
Современное значение определяется по формуле сложной учетной ставки:

Ответ: Современное значение составляет 80 688 р.
Задача 2.1.9.
Какая сумма образуется в банке через 2 года, если в банк положено 10 тыс. р. под 12 % годовых, начисляемых ежеквартально?
Методические указания: использовать формулу (2.1.8).
Дано:
Решение:
Проценты начисляются ежеквартально, т. е. 4 раза в год (m = 4). В этой ситуации будущая стоимость определяется:
Ответ: В банке накопится сумма 8157,3 р.
Задача 2.1.10.
Выдан кредит 200 тыс. р. на I квартал под 25 % годовых. В случае просрочки возврата долга процентная ставка увеличивается на 5 % в каждом следующем квартале и начисляется на наращенную сумму. Долг возвращается через год. Какую сумму следует вернуть?
Методические указания: ввести дополнительные обозначения:
использовать формулу (2.1.7).
Дано:

Решение:
Находим ставки наращения по кварталам:




Будущую стоимость находим по схеме сложных процентов с учетом того, что в каждом периоде ставки разные:
Ответ: В случае возврата долга через год следует вернуть 273,3 тыс. р.
Задача 2.1.11.
Какие условия вклада более выгодные: 1) 12 % годовых с ежеквартальным начислением; 2) 11 % годовых с ежемесячным начислением; 3) 12,5 % с начислением в конце года?
Методические указания: использовать формулу (2.1.9).
Дано:

Решение:
Для сравнения вкладов с разными сроками начисления необходимо рассчитать эффективную ставку:


Ответ: Наиболее выгоден первый вклад, т. к. фактически он дает 12,55 % годовых, менее всего выгоден второй вклад, дающий 11,57 % годовых.
Задача 2.1.12.
Рассчитать все возможные оценки денежного потока, включающего четыре последовательные выплаты в объеме 200, 180, 150 и 190 тыс. р. в год при процентной ставке 15 %.
Методические указания: использовать формулы (2.1.4), (2.1.5), (2.1.11) — (2.1.14).
Дано:
Решение:
Поскольку в условии не уточняется, какую схему наращения следует использовать, рассмотрим оба варианта.
По схеме сложных процентов дисконтирование осуществляется по формулам (2.1.13) и (2.1.14):
1) настоящая стоимость потока постнумерандо:
2) настоящая стоимость потока пренумерандо:
Можно увидеть, что 

3) будущая стоимость постнумерандо:
4) будущая стоимость пренумерандо:
Можно увидеть, что 

Ответ: 


Определим стоимость денежного потока при условии начисления простых процентов:
1) настоящая стоимость потока постнумерандо:
2) настоящая стоимость потока пренумерандо:
3) будущая стоимость потока постнумерандо:
4) будущая стоимость потока пренумерандо:
Ответ: 


Обратите внимание: настоящая стоимость при начислении простых процентов больше, чем при начислении сложных, а будущая стоимость при начислении простых процентов меньше, чем при начислении сложных.
Задача 2.1.13.
Сколько нужно вложить в банк под 25 % годовых, чтобы в течение 4 лет получать выплаты по 100 тыс. р.?
Методические указания: использовать формулу (2.1.15).
Дано:
Решение:
Поскольку выплаты равномерные, то воспользуемся формулой для нахождения настоящей стоимости аннуитета постнумерандо:
Ответ: Следует вложить 236 160 р.
График начислений процентов и выплат представлен в табл. 2.1.1.
Таблица 2.1.1 — Начисление процентов и ежегодные выплаты, р.
Сумма на начало года
Начисленная сумма процентов
Сумма на конец года
Выплата в конце года
Задача 2.1.14.
Методические указания: использовать формулы (2.1.15) и (2.1.16).
Дано:
Решение:
Выплаты осуществляются в начале каждого года, т. е. данная аренда порождает поток пренумерандо:
Задача 2.1.15.
Методические указания: использовать формулы (2.1.15) и (2.1.17).
Дано:
Решение:
Вначале определяются ежегодные платежи по возврату долга. Поскольку долг возвращается равными платежами, этот денежный поток рассматривается как постоянный аннуитет. Из формулы настоящей стоимости аннуитета постнумерандо (2.1.15) можно найти размер ежегодного платежа:
Для расчета суммы, накопленной в банке следует воспользоваться формулой будущей стоимости аннуитета постнумерандо:
Задача 2.1.16.
Рассчитать стоимость аренды при ежегодной выплате 15 тыс. р. и процентной ставке 10 %: а) на срок 10 лет, б) бессрочной
Методические указания: использовать формулы (2.1.15) — (2.1.19).
Дано:
Решение:
Для каждого срочного денежного потока можно рассчитать четыре оценки:
1) настоящая стоимость аренды постнумерандо (при оплате аренды в конце каждого года):
2) настоящая стоимость аренды пренумерандо (при оплате аренды в начале каждого года):
3) Будущая стоимость аренды постнумерандо:
4) будущая стоимость аренды пренумерандо:
Оценки бессрочной аренды:
Ответ: 


Задача 2.1.17.
Определить размер равномерных выплат при возврате долга, если сумма долга 150 тыс. р. на 4 года, процентная ставка 11 % годовых.
Методические указания: использовать формулу (2.1.15).
Дано:
Решение:
При условии возврата долга равными долями в конце каждого года соответствующий денежный поток представляет собой постоянный аннуитет, постнумерандо, размер платежа по которому определяется из формулы настоящей стоимости аннуитета:

Ответ: Ежегодный размер выплат составит 48,4 тыс. р.
Замечание: Следует обратить внимание на структуру платежа, которая меняется год от года (табл. 2.1.2).
Таблица 2.1.2 — Структура ежегодных платежей
Остаток долга на начало года
Сумма в счет погашения долга
Задачи для самостоятельного решения
Задача 2.1.18.
Определить, чему равны учетная и процентная ставки при возрастании стоимости за год с 10 до 18 тыс. р.
Методические указания: использовать формулы (2.1.1), (2.1.2).
Задача 2.1.19.
Рассчитать все возможные оценки денежного потока, включающего четыре последовательных выплаты в объеме (200, 180, 250, 220, 190) тыс. р. в год при процентной ставке 13 %.
Методические указания: использовать формулы (2.1.4), (2.1.5), (2.1.11) — (2.1.14).
Задача 2.1.20.
Рассчитать стоимость аренды при ежегодной выплате 25 тыс. р. и процентной ставке 12 %: а) на срок 15 лет, б) бессрочной.
Методические указания: использовать формулы (2.1.15) — (2.1.19).
Задача 2.1.21.
Выдан кредит 100 тыс. р. на полугодие под 30 % годовых. В случае просрочки возврата долга процентная ставка увеличивается на 3 % в каждом следующем полугодии и начисляется на наращенную сумму. Долг возвращается через 1,5 года. Какую сумму следует вернуть?


использовать формулу (2.1.7).
Задача 2.1.22.
Сколько нужно вложить в банк для получения через 4 года 500 тыс. р. под 12 % годовых: а) без капитализации, б) с капитализацией?
Задача 2.1.23.
Рассчитать учетную ставку, которая обеспечивает получение 8 млн р., если сумма в 8,5 млн р. выдается в ссуду на один квартал.
Методические указания: использовать формулу (2.1.6).
Задача 2.1.24.
Сколько нужно вложить в банк под 15 % годовых, чтобы в течение 5 лет получать выплаты по 100 тыс. р.?
Методические указания: использовать формулу (2.1.15).
Задача 2.1.25.
Какая сумма будет в банке через 4 года, если вложено 110 тыс. р. под 12 % годовых: а) без капитализации, б) с капитализацией?
Методические указания: использовать формулы (2.1.3), (2.1.5), (2.1.7).
Задача 2.1.26.
Определить современное значение суммы в 150 тыс. р., которая будет выплачена через 2 года при использовании сложной учетной ставки 15 % годовых.
Методические указания: использовать формулы (2.1.6), (2.1.7).
Задача 2.1.27.
Методические указания: использовать формулы (2.1.15) и (2.1.16).
Задача 2.1.28.
Определить размер равномерных выплат при возврате долга, если сумма долга 200 тыс. р. на 3 года, процентная ставка 12 % годовых.
Методические указания: использовать формулу (2.1.15).
Задача 2.1.29.
Под какой процент следует вложить 50 тыс. р., чтобы получить 150 тыс. р. через 5 лет?
Методические указания: использовать формулы (2.1.5), (2.1.7).
Задача 2.1.30.
Какие условия вклада более выгодные: 1) 13 % годовых с ежеквартальным начислением; 2) 12 % годовых с ежемесячным начислением; 3) 14 % с начислением в конце года?
Методические указания: использовать формулу (2.1.9).
Задача 2.1.31.
Кредит выдается под простую ставку 20 % годовых на 280 дней. Рассчитать сумму, получаемую заемщиком, и сумму процентных денег, если требуется возвратить 35 тыс. р.
Методические указания: использовать формулы (2.1.5), (2.1.6).
Задача 2.1.32.
Определить период начисления, за который первоначальный капитал в размере 35 тыс. р. вырастет до 50 тыс. р., если используется простая процентная ставка 25 % годовых.
Методические указания: использовать формулу (2.1.5).
Задача 2.1.33.
Методические указания: использовать формулы (2.1.15) и (2.1.17).
Задача 2.1.34.
Какая сумма образуется в банке через 2,5 года, если в банк положена 1000 р. под 13 % годовых, начисляемых ежеквартально?
Методические указания: использовать формулу (2.1.8).
2.2. Методы оценки финансовых активов
В данном параграфе используются следующие обозначения:
A — одинаковый ежегодный (ежеквартальный, ежемесячный и т. п.) приток/отток денег (выплаты, арендная плата), ден. ед.;
D — доход, дивиденд, ден. ед.;

d — учетная ставка, доходность, %;
F — будущая стоимость (вклада, будущая сумма возвращаемого долга), ден. ед.;
g — темп прироста дивиденда, %;
k — количество периодов, лет, месяцев, дней;
m — число начислений в год, разы;
n — срок аренды (выплат, погашения долга, денежного потока), годы, месяцы, дни;
P — настоящая стоимость (вклада, долга), ден. ед.;
r — процентная ставка (ставка наращения, ставка дисконтирования), %;
re— эффективная процентная ставка, %;
V — внутренняя стоимость;
аор — акция обыкновенная с равномерным ростом дивиденда;
аон — акция обыкновенная с неравномерным ростом дивиденда;
ап — привилегированная акция;
апв — акция привилегированная выкупная;
он — облигация с нулевым купоном;
об — облигация бессрочная;
опд — облигация безотзывная с постоянным доходом.
Задача 2.2.1.
Определить курсовую стоимость привилегированной акции, номинал которой 300 р., ставка дивиденда 25 %. Банковская ставка процента 20 %.
Методические указания: использовать формулу (2.2.5).
Дано:
Решение:
Исходя из предположения, что курсовая стоимость отражает внутреннюю стоимость акции, курсовую стоимость можно найти следующим образом:
Ответ: Курсовая стоимость акции составляет 375 ру.
Задача 2.2.2.
Методические указания: использовать формулу (2.2.5).
Дано:
Решение:
Постоянный регулярный доход, который приносит сдача в аренду имущества, по существу представляет собой денежный поток, аналогичный потоку дивидендов, порождаемому привилегированной акцией.
В связи с этим можно воспользоваться формулой оценки внутренней стоимости привилегированной акции:
Задача 2.2.3.
Последний выплаченный дивиденд составил 200 р. на одну акцию. Ожидается рост дивидендов со среднегодовым темпом прироста 5 %. Среднерыночная доходность акций аналогичного класса риска составляет 10 %. Определить целесообразность покупки акции, если ее цена на рынке составляет 4,5 тыс. р.
Методические указания: использовать формулу (2.2.8).
Дано:
Решение:
Оценка внутренней стоимости акции с равномерно возрастающим дивидендом рассчитывается с помощью формулы Гордона:
Далее необходимо сравнить цену и внутреннюю стоимость акции:
Р = 4500 р. > 4200 p. = V аор.
Ответ: Внутренняя стоимость акции меньше рыночной цены, поэтому покупка акции нецелесообразна.
Задача 2.2.4.
Методические указания: использовать формулы (2.2.4), (2.2.5) и (2.2.10).
Дано:
Решение:
В данном случае внутренняя стоимость акции складывается из двух слагаемых — первое (для первых 4 лет) на основе формулы (2.2.4); второе — для 5-го и последующих периодов на основе формулы (2.2.5) с учетом дисконтирования. Итоговая формула для оценки внутренней стоимости акции в данном случае примет вид:
Сравним внутреннюю стоимость и цену — цена выше.
Ответ: Поскольку цена выше внутренней стоимости, продажа акции целесообразна (при возможности вложения денег в другие финансовые инструменты со среднерыночной доходностью 12 % и аналогичным классом риска).
Задача 2.2.5.
Методические указания: использовать формулы (2.1.15), (2.2.10).
Дано:
Решение:
Для определения внутренней стоимости акции воспользуемся формулой (2.2.10) с учетом того, что в первые 3 года денежный поток представляет собой постоянный аннуитет (формула 2.1.15):
Для ответа на вопрос о целесообразности покупки акции необходимо сравнить рыночную цену и внутреннюю стоимость акции:
Задача 2.2.8.
Какова теоретическая стоимость бессрочной облигации с годовым доходом 500 р. при приемлемой прибыльности 17 %?
Методические указания: использовать формулу (2.2.12).
Дано:
Решение:
Ответ: Теоретическая стоимость бессрочной облигации составляет 2941 рубль.
Задача 2.2.9.
Рассчитать внутреннюю стоимость облигации, выпущенную на 4 года номиналом 1 тыс. р. Купонная ставка 15 % годовых, доход выплачивается дважды в год. Среднерыночная ставка — 10 %. Проанализировать зависимость внутренней стоимости от среднерыночной ставки процента.
Методические указания: использовать формулы (2.1.9), (2.1.15) и (2.2.13).
Дано:
Решение:
Модифицируем формулу (2.2.13) с использованием формул (2.1.9) и (2.1.15):
Рассмотрим, как изменится внутренняя стоимость облигации при увеличении среднерыночной ставки процента, например, до 18 %:
При увеличении среднерыночной ставки процента внутренняя стоимость финансового инструмента уменьшается, и наоборот, при уменьшении среднерыночной ставки внутренняя стоимость увеличивается.
Обратите внимание, что если среднерыночная ставка равна купонной ставке, то внутренняя стоимость облигации равна номиналу:
Ответ: Внутренняя стоимость облигации равна 1162 р. Внутренняя стоимость облигации имеет обратную зависимость от среднерыночной ставки процента.
Задача 2.2.10.
Рассчитать внутреннюю стоимость облигации, выпущенную на 4 года номиналом 1 тыс. р. Купонная ставка 15 % годовых, доход выплачивается один раз в год. Проанализировать изменение внутренней стоимости облигации во времени по мере приближения срока погашения 1) в случае, если купонная доходность меньше среднерыночной ставки процента, 2) в случае, если купонная доходность больше среднерыночной ставки процента; 3) в случае, если купонная доходность равна среднерыночной ставке процента.
Методические указания: использовать формулу (2.2.13).
Дано:
Решение:
Рассмотрим три варианта среднерыночной ставки процента: 
Предварительно рассчитаем вспомогательные величины (табл. 2.2.1).
Таблица 2.2.1 — Коэффициенты дисконтирования



Начнем со среднерыночной ставки, равной купонной доходности облигации, т. е. 15 %. Рассчитаем внутреннюю стоимость облигации на момент выпуска:
Рассчитаем внутреннюю стоимость облигации через год:
Аналогичный результат получим через 2 и 3 года. Т. е. в этом случае внутренняя стоимость облигации не меняется и остается равной номиналу.
Рассчитаем внутреннюю стоимость облигации на момент выпуска при рыночной ставке 10 %:
Рассчитаем внутреннюю стоимость облигации через год:
Рассчитаем внутреннюю стоимость облигации через 2 года:
Рассчитаем внутреннюю стоимость облигации через 3 года:
Через 4 года облигация погашается по номиналу.
Аналогичным образом рассчитаем внутреннюю стоимость облигации при среднерыночной ставке 20 %. Результаты расчетов занесем в табл. 2.2.2.
Таблица 2.2.2 — Динамика внутренней стоимости облигации
Среднерыночная ставка процента
Внутренняя стоимость облигации
Ответ: Значения внутренней стоимости облигации на разные моменты времени и при разных среднерыночных ставках процента приведены в табл. 2.2.2. При среднерыночной ставке процента больше купонной ставки внутренняя стоимость облигации со временем повышается. При среднерыночной ставке процента меньше купонной ставки внутренняя стоимость облигации со временем понижается.
Задачи для самостоятельного решения
Задача 2.2.11.
Последний выплаченный дивиденд составил 300 р. на одну акцию. Ожидается рост дивидендов со среднегодовым темпом прироста 4 %. Среднерыночная доходность акций аналогичного класса риска составляет 15 %. Определить целесообразность покупки акции, если ее цена на рынке составляет 3,5 тыс. р.
Методические указания: использовать формулу (2.2.8).
Задача 2.2.12.
Оценить целесообразность вложения денежных средств в пакет облигаций, если известно: номинал пакета — 50 тыс. руб., цена погашения равна номиналу, купонный процент по облигациям не выплачивается. Сегодня пакет можно приобрести за 40 тыс. руб. Срок погашения пакета — через 3 года. Инвестора устроит доходность не менее 20 % годовых.
Методические указания: использовать формулу (2.1.7).
Задача 2.2.13.
Методические указания: использовать формулу (2.2.5).
Задача 2.2.14.
Какова теоретическая стоимость бессрочной облигации с годовым доходом 600 р. при приемлемой прибыльности 18 %?
Методические указания: использовать формулу (2.2.12).
Задача 2.2.15.
Методические указания: использовать формулу (2.2.5).
Задача 2.2.16.
Облигация с нулевым купоном, выпущенная на срок 4 года, продается за 750 р. Номинальная цена облигации 1 тыс. р. Среднерыночная доходность финансовых инструментов аналогичного класса риска составляет 10 %. Выгодна ли покупка?
Методические указания: Вопрос о целесообразности покупки можно решать: 1) путем сравнения внутренней стоимости и цены, 2) путем сравнения среднерыночной и реальной доходносткй облигации. Рассмотрите оба варианта, для чего необходимо использовать формулы (2.2.11) и (2.1.7).
Задача 2.2.17.
Методические указания: использовать формулы (2.2.4), (2.2.5) и (2.2.10).
Задача 2.2.18.
Рассчитать внутреннюю стоимость облигации, выпущенной на 3 года номиналом 800 р. Купонная ставка 10 % годовых, доход выплачивается один раз в год. Проанализировать изменение внутренней стоимости облигации во времени по мере приближения срока погашения: 1) при среднерыночной ставке процента 8 %, 2) при среднерыночной ставке процента 13 %; 3) при среднерыночной ставке процента 10 %.
Задача 2.2.19.
Методические указания: использовать формулы (2.1.15), (2.2.10).
Задача 2.2.20.
Рассчитать внутреннюю стоимость облигации, выпущеннорй на 5 лет номиналом 1200 р. Купонная ставка 10 % за полугодие, доход выплачивается дважды в год. Среднерыночная ставка — 18 %.
Методические указания: использовать формулы (2.1.9), (2.1.15) и (2.2.13).
2.3. Риск в финансовом менеджменте
В данном параграфе используются следующие обозначения:
CV — коэффициент вариации;


n — количество вариантов;
Задача 2.3.1.
Оценить риск покупки валюты, если курс за последние полгода колебался в диапазоне от 10 до 14 р. без явно выраженной тенденции к росту или падению. Статистические характеристики изменения курса приведены в табл.2.3.1.
Таблица 2.3.1 — Характеристика изменчивости курса валюты
Номер варианта (j)
Курс (
Количество дней (
Методические указания: использовать формулы (2.3.1) — (2.3.3).
Дано:

Решение:
Мерой риска может выступать среднеквадратическое отклонение курса от среднего — σ, а также коэффициент вариации — CV, в основе которых лежит расчет дисперсии:

Для использования данной формулы необходимо рассчитать среднее значение курса валюты, а также частоты.
Среднее значение курса равно:
Находим частоты курсов:
Подставляем полученные результаты в формулу для расчета дисперсии:
Среднеквадратическое отклонение равно:


Ответ: Риск покупки валюты может быть охарактеризован дисперсией, равной 1,94; среднеквадратическим отклонением 1,39 р.; коэффициентом вариации 11,3 %.
Задача 2.3.2.
Известный аналитический центр опубликовал данные по ценным бумагам компаний (табл. 2.3.2). Необходимо выбрать объект вложений.
Таблица 2.3.2 — Прогноз доходности ценных бумаг трех компаний
Вероятность,
Методические указания: Принятие решения о вложении средств основывается на расчете ожидаемой доходности, дисперсии и коэффициента вариации по каждой ценной бумаге каждой компании. В решении необходимо использовать формулы (2.3.1) — (2.3.3).
Дано:
Найти:
Решение:
Прежде всего находим среднюю ожидаемую доходность ценных бумаг каждой компании:
Наиболее доходными являются ценные бумаги А(1).
С помощью полученных значений найдем дисперсию доходности по каждой ценной бумаге:
Из полученных дисперсий найдем СКО для каждой компании:
Минимальной дисперсией и соответственно минимальным среднеквадратическим отклонением характеризуются ценные бумаги компании А(1). Однако уровень колеблемости (риска) следует оценивать по отношению к среднему ожидаемому значению, для чего необходимо рассчитать коэффициенты вариации доходности ценных бумаг каждой компании:
Коэффициент вариации имеет минимальное значение также для ценных бумаг компании А(1).
На рис. 2.3.1 представлены средние, максимальные и минимальные доходности ценных бумаг трех компаний.
Рисунок 2.3.1 — Распределение доходностей акций трех компаний
Ответ: Нужно вкладываться в ценные бумаги А(1), т. к. они наиболее доходны и наименее рисковы.
Задачи для самостоятельного решения
Задача 2.3.3.
Оценить риск покупки валюты, если курс за последние полгода колебался в диапазоне от 9 до 15 р. без явно выраженной тенденции к росту или падению. Статистические характеристики изменения курса приведены в табл. 2.3.3.
Таблица 2.3.3 — Характеристика изменчивости курса валюты
Номер варианта (j)
Курс (
Количество дней (
Методические указания: использовать формулы (2.3.1) — (2.3.3).
Задача 2.3.4.
Выбрать объект вложений, исходя из данных по ценным бумагам компаний, представленных в табл. 2.3.4.
Таблица 2.3.4 — Прогноз доходности ценных бумаг трех компаний
Компания (i)
Ситуация
Вероятность,
Доходность %,
Методические указания: Принятие решения о вложении средств основывается на расчете ожидаемой доходности, дисперсии и коэффициента вариации по каждой ценной бумаге каждой компании. В решении необходимо использовать формулы (2.3.1) — (2.3.3).
2.4. Принятие решений в условиях риска и неопределенности
В данном параграфе используются следующие обозначения:
А* — оптимальное решение;
bij — величина сожаления при выборе i-го варианта в случае, если среда пребывает в j- м состоянии;
f (Ai) — оценка i-го варианта по какому-либо критерию;
f (A*) — максимальное значение критерия при оптимальном решении;
a — коэффициент оптимизма;
Зпер — затраты переменные;
Зпст — затраты постоянные.
Задача 2.4.1.
В пункте проката выдаются в прокат холодильники. Оборудование это дорогое и, очевидно, его простой влечет за собой убытки.
Спрос на холодильники есть величина случайная, которая зависит от множества различных факторов.
Какое количество холодильников необходимо иметь в пункте проката, если известно, что:
Какое решение следует принять, если известно распределение вероятностей спроса (табл. 2.4.1).
Таблица 2.4.1 — Вероятности спроса на холодильники
Методические указания: Первый шаг решения задачи — это выбор возможных вариантов решения. Очевидно, при предположении, что спрос колеблется в диапазоне от 5 до 30 возможных вариантов — 26 (5, 6, 7 и т. д. до 30). Однако обычно рассматриваются не все, а несколько вариантов. Например: 5, 10, 15, 20, 25 и 30 холодильников. И такие же варианты спроса. Решим задачу при этих предположениях. В ходе решения следует использовать формулы (2.4.1) — (2.4.7) для принятия решений по разным правилам (критериям). Необходимо принять решение по всем критериям (по каждому отдельно).
При этом следует помнить, что в реальности для принятия решений следует использовать только одно правило, соответствующее предпочтениям лица, принимающего решения.
Дано:
Зпер = 1200 р./год на один хол.
D = 300 р./мес. на один хол.
Решение:
Рассмотрим 6 возможных вариантов решений А1=5, А2=10, А3=15, А4=20, А5=25, А6=30 и 6 возможных состояний среды (значений спроса): Z1=5, Z2=10, Z3=15, Z4=20, Z5=25, Z6=30.
В условиях риска и неопределенности для принятия решений строится матрица решений (в данном случае — матрица прибыли). Расчет элементов матрицы осуществляется по следующей формуле:
При использовании данной формулы следует помнить, что доход зависит не только от спроса, но и от того, сколько холодильников имеется в пункте проката, поэтому при расчете дохода используется минимальное из двух значений: наличия и спроса на холодильники.
Рассчитаем некоторые элементы матрицы прибыли:
f(A1,Z1) = –20 000 – 1200 х 5 + 300 х 12 х 5 = –8 тыс. р.;
Аналогичным образом рассчитываются остальные элементы (табл. 2.4.2).
Таблица 2.4.2 — Матрица прибыли (тыс. р.)
По критерию Вальда для каждого действия (в каждой строке) необходимо выбрать наихудший результат (минимальную прибыль), а затем из них выбрать лучший (максимальную прибыль из минимальных), используя формулу (2.4.3):
Это означает, что при принятии решения о наличии 5 холодильников в пункте проката в худшем случае убыток составит 8 тыс. рублей в год.
Аналогично рассчитываются все f(Ai) (см. табл. 2.4.4).
Далее выбирается решение, максимизирующее ожидаемую прибыль:
Таким образом, при пессимистическом прогнозе открывать прокат холодильников не следует, т. к. даже при минимальном количестве холодильников доход не достаточен для покрытия расходов. При наличии 5 холодильников убыток составляет 8 тыс. рублей в год.
По критерию оптимизма необходимо выбрать наилучший из всех возможных результатов всех действий (сначала максимум в каждой строке, а потом максимум из максимумов):
Это означает, что при принятии решения о наличии 5 холодильников в пункте проката в лучшем случае убыток составит 8 тыс. рублей в год.
Аналогично рассчитываются все f (Ai) (см. табл. 2.4.4).
Далее выбирается решение максимизирующее ожидаемую прибыль:
Таким образом, при оптимистическом прогнозе в пункте проката следует иметь 30 холодильников, т. к. в этом случае получается максимальная прибыль 52 тыс. р. в год.
По критерию Гурвица необходимо найти среднюю взвешенную оценку наилучшего и наихудшего результатов по каждому действию, где в качестве веса выступает коэффициент оптимизма (формула 2.4.4). Для примера рассмотрим a =0,8:
Это означает, что при принятии решения о наличии 25 холодильников в пункте проката ожидается прибыль 25,6 тыс. р. в год.
Аналогично рассчитываются все f(Ai) (см. табл. 2.4.4).
Далее выбирается решение максимизирующее ожидаемую прибыль:
По критерию Гурвица при a =0,8 следует в пункте проката иметь 30 холодильников, при этом ожидается прибыль 34 тыс. рублей в год.
По критерию Лапласа необходимо найти среднюю оценку всех возможных результатов по каждому действию (формула 2.4.5), например:
Это означает, что при принятии решения о наличии 20 холодильников в пункте проката ожидается прибыль 10 тыс. рублей в год.
Аналогично рассчитываются все f(Ai) (см. табл. 2.4.4).
Далее выбирается решение, максимизирующее ожидаемую прибыль:
В случае если максимальная прибыль ожидается по двум вариантам — 20 и 25 холодильников, следует использовать критерий осторожности (Вальда) для выбора из этих вариантов. По критерию Вальда: f(A4=20)=-26 > f(A5=25)=-32, следовательно, необходимо выбрать четвертый вариант — 20 холодильников.
Для использования критерия Сэвиджа необходимо рассчитать матрицу сожалений (табл. 2.4.3), используя формулу (2.4.6): в каждом столбце матрицы прибыли выбирается максимальный элемент, из которого последовательно вычитаются все элементы рассматриваемого столбца, например:
Аналогично рассчитываются все bij (см. табл. 2.4.3).
Затем выбираются максимальные сожаления для каждого варианта решения (формула 2.4.7):
Аналогично выбираются все bi (см. табл. 2.4.3).
Таблица 2.4.3 — Матрица сожалений
Далее выбирается минимум из выбранных вариантов:
Поскольку минимальное сожаление ожидается по двум вариантам — 20 и 25 холодильников, следует также использовать критерий осторожности (Вальда) для выбора из этих вариантов. По критерию Вальда: f(A4=20)=–26 > f(A5=25)=–32, следовательно, необходимо выбрать четвертый вариант — 20 холодильников.
В табл. 2.4.4 сведены все решения.
Таблица 2.4.4 — Ожидаемая прибыль по разным правилам (критериям)
В случае если известны вероятности спроса, решение находится, исходя из расчета математического ожидания прибыли (2.4.2):
f(A2) = 0,05 х (–14) + (0,2 + 0,3 + 0,2 + 0,15 + 0,1) х 4 = 3,1
f(A3) = 0,05 х (–20) + 0,2 х (–2) + (0,3 + 0,2 + 0,15 + 0,1) х 16 = 10,6
f(A4) = 0,05 х (-26) + 0,2 х (-8) + 0,3 х 10 + (0,2 + 0,15 + 0,1) х 28 = 12,7
f(A5) = 0,05 х (-32) + 0,2 х (-14) + 0,3 х 4 + 0,2 х 22 + (0,15 + 0,1) х 40 = 15,2
f(A6) = 0,05 х (-38) + 0,2 х (-20) + 0,3 х (-2) +0,2 х 16 +0,15 х 34 + 0,1 х 52 = 7.
Максимум ожидаемой прибыли 15,2 тыс. р. в год получается при принятии решения о наличии 25 холодильников в пункте проката.
Ответ: По критерию Вальда не следует открывать прокат холодильников.
По критерию Гурвица при коэффициенте оптимизма 0,8 следует иметь 30 холодильников.
При заданном распределении вероятностей (табл. 2.4.1) лучшим является решение о наличии 25 холодильников.
Задачи для самостоятельного решения
Методические указания: при решении задач 2.4.2 — 2.4.10 пользуйтесь методическими указаниями к задаче 2.4.1.
Задача 2.4.2.
Необходимо построить консервную фабрику по переработке овощей. Имеются проекты строительства в расчете на разную мощность: 10, 20, 30, 40, 50 тыс. т в год. Затраты на строительство вне зависимости от мощности составляет 420 млн руб. Кроме того, затраты на каждую 1 тыс. т мощности — 2 млн руб. Известно, что урожайность овощей может принимать значения от 10 до 50 тыс. т в год. Доход от переработки 1 т овощей 20 тыс. р.
Какой проект следует принять?
Задача 2.4.3.
В парке культуры решено организовать лодочную станцию. Затраты на содержание лодочной станции вне зависимости от количества лодок составляют 80 тыс. р. в сезон (100 дней). Содержание каждой лодки на лодочной станции в сезон составляет 2 тыс. р. Предполагается, что лодочная станция будет работать каждый день по 10 ч. Прокат лодки в час стоит 30 р. Известно, что спрос на лодки колеблется от 5 до 25 в час.
Какое количество лодок (10, 15, 20, 25) должно быть на станции?
Задача 2.4.4.
В городке аттракционов строится колесо обозрения. Имеются проекты с 30, 40, 50, 60 кабинами. В каждой кабине 4 места. Предполагается, что ежедневно будет проводиться 10 рейсов. Затраты на содержание колеса вне зависимости от количества посетителей составляют 3 тыс. р. в день. Кроме того, каждые 10 кабинок приводят к возрастанию затрат на 1000 руб. ежедневно. Число посетителей может составлять в среднем 120, 160, 200, 220 человек на каждый рейс. Стоимость билета 20 руб.
Какой проект принять?
Задача 2.4.5.
Требуется построить кинотеатр. Имеются проекты на 600, 700, 800, 900 мест. Затраты на содержание кинотеатра составляют 4 тыс. р. в день. Дополнительные затраты на содержание каждых 100 мест составляют 1000 руб. в день. Планируется проведение 6 сеансов ежедневно. Цена билета 120 руб. Известно, что число занятых мест в сеанс может быть 500, 600, 700, 800, 900.
Какой проект следует выбрать?
Задача 2.4.6.
Строится гараж для легковых автомобилей. Требуется определить, на сколько мест строить гараж, если сведений о количестве автомобилей у жителей района нет. Предполагается, что это случайная величина, определенная на интервале от 50 до 200. Затраты на строительство, не зависящие от числа мест, составляют 3 млн. руб., затраты на каждое место — 100 тыс. р., выплачиваются равномерно в течение 10 лет. Доход, получаемый от эксплуатации гаража, составляет 4 тыс. р. на одно занятое место в год.
Задача 2.4.7.
На вновь организованную выставку требуются экскурсоводы. Каждый экскурсовод может провести 4 экскурсии в день (каждая экскурсия по 25 человек). Затраты на содержание выставки составляют 3500 руб. в день. Зарплата экскурсовода — 1200 руб. в день. Ежедневно выставку могут посетить 50, 100, 150, 200, 250, 300 человек. Цена билета 50 руб.
Сколько требуется экскурсоводов?
Задача 2.4.8.
Возле станции метро решено построить павильон по продаже мороженого. Затраты на содержание павильона составляют 1000 р. в день. Известно, что один продавец может продать в день до 400 штук мороженого. Средний доход от продажи одного мороженого составляет 3 руб. Затраты на одного продавца составляют 600 руб. в день. Спрос колеблется от 300 до 1200 шт. мороженого в день (300, 600, 900, 1200).
Сколько продавцов следует нанять?
Задача 2.4.9.
Организуется прокат детских автомобилей. Затраты на содержание станции составляют 270 тыс. р. в сезон. Сезон — 90 дней. Затраты на содержание каждого автомобиля составляют 9 тыс. р. в сезон. Прокат одного автомобиля стоит 100 р. Каждый автомобиль может сдаваться в прокат 4 раза в день. Предполагается, что количество желающих покататься колеблется в диапазоне от 20 до 100 (20, 40, 60, 80, 100) в день. (Составить матрицу прибыли в день)
Сколько автомобилей следует иметь на станции?
Задача 2.4.10.
Открывается парикмахерская. Затраты, не зависящие от числа рабочих мест, составляют 10 тыс. р. в месяц. Месяц — 25 рабочих дней. Содержание каждого рабочего места увеличивает затраты на 3 тыс. р. в месяц. Зарплата одного парикмахера — 16 тыс. р. в месяц. Стоимость одной прически — 500 руб. Каждый парикмахер может обслужить в день 20 клиентов. Ожидается от 20 до 60 клиентов в день (20, 30, 40, 50, 60).
Сколько нужно парикмахеров?
Задача 2.4.11.
В районе новостроек решено организовать курсы иностранных языков. Аренда помещения на полгода стоит 250 тыс. р. Зарплата одного педагога — 12 тыс. р. в месяц. Один преподаватель может обучать группу в 30 человек. Каждый обучающийся должен внести плату за полугодовой курс 15 тыс. р. Количество желающих прогнозируется от 30 до 150 человек.
Сколько групп следует открыть?
2.5. Риск и доходность финансовых активов
Задача 2.5.1.
Оценить доходность облигации с купонным доходом 8 % год, которая продается за 5 тыс. р. Через 5 лет облигация будет погашена по номиналу 5500 р.
Методические указания: 1) ввести обозначения: N — номинальная цена облигации; P — рыночная цена облигации на момент покупки;

2) использовать формулу (2.5.3).
Дано:

Решение:
Доходность — это отношение среднегодового дохода к инвестициям (затратам). Среднегодовой доход от облигации складывается из годового купонного дохода и среднегодового прироста стоимости облигации:
Ответ: Среднегодовая доходность облигации 10,2 %.
Задача 2.5.2.
Определить ожидаемую доходность акции, которая продается по цене 1200 р., ожидаемый дивиденд 600 р. Инвестор предполагает продать акцию через 2 года по цене 2 тыс. р.
Методические указания: 1) ввести обозначения: da — доходность акции; dat — текущая (дивидендная) доходность акции; dac — капитализированная доходность акции; 


2) использовать формулу (2.5.7).
Дано:


Решение:
Текущая доходность акции:


Ответ: Доходность акции 88,3 % годовых.
Задача 2.5.3.
Определить ожидаемую доходность акции, которая продается по цене 1500 р., полученный дивиденд 300 р., ожидается равномерный рост дивиденда 4 % в год.
Методические указания: 1) ввести обозначения: da — доходность акции; dat — текущая (дивидендная) доходность акции; dac — капитализированная доходность акции; 



2) использовать формулу (2.5.8).
Дано:



Решение:
Для оценки значений ожидаемой общей доходности обыкновенных акций с равномерно возрастающими дивидендами можно воспользоваться формулой Гордона:
Ответ: Доходность акции 24,8 % годовых.
Задача 2.5.4.
Рассчитать премию за риск, которую необходимо учитывать при оценке внутренней стоимости инструмента. Данные о доходности рассматриваемого финансового инструмента и о среднерыночной доходности данной группы финансовых инструментов представлены в табл. 2.5.1. Безрисковая доходность 10 %. Оценить ожидаемую доходность финансового инструмента.
Таблица 2.5.1 — Доходность финансовых инструментов
 а.
а.








































































































