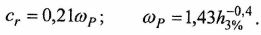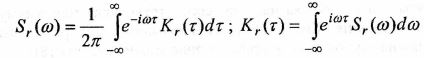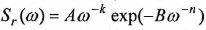Волна 3 обеспеченности что это такое

ХАРАКТЕРИСТИКИ НЕРЕГУЛЯРНОГО ВОЛНЕНИЯ

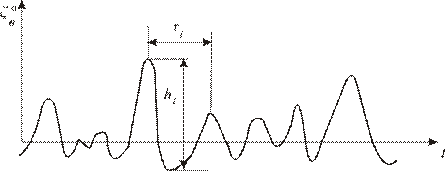
Образец записи (реализации) нерегулярного волнения изображен на рис. 2.2. Как мы видим, каждая последующая волна отличается от предыдущей по высоте и периоду, т.е. по длине. Если обозначить высоту какой-либо волны h_i, амплитуда волны по определению будет равна

r_i= .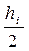

Существуют три метода описания нерегулярного волнения: статистический, спектральный и корреляционный. В практических расчетах применяются в основном статистический и спектральный методы. Рассмотрим их более подробно.

Рис. 2.2. Реализация нерегулярного волнения.

Статистический метод.

p_i = 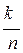, (2.20)

Оценка интенсивности волнения производится с помощью дисперсии (квадрата среднего квадратичного отклонения)

D_r = 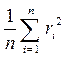. (2.21)

Средняя высота волны (в вероятностном смысле) связана с дисперсией соотношением

= 2,5 . (2.22)

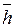
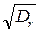
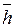
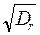
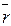
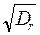
h_46,5% = = 2,5 ; r_46,5% = = 1,25 . (2.22¢)

В таблицах балльности волн обычно выписываются значения h_3%,, для которых

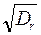
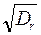
h_3% = 5,3 ; r_3% = 2,65 . (2.23)

Иногда необходимо определить дисперсию волны, зная высоту h_3%.. Из (2.23) следует

D_r = 0,143 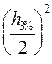. (2.24)

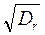
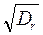
h_max = h_0,5% = 6,5 ; r_max = r_0,5% = 3,25 . (2.25)

Таблица 2.1. Баллы ветрового волнения

Баллы волн	Баллы ветра	Длина волн 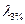, м	Высота волн 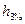, м	Период волн 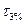, с	Словесная характеристика
0-1	отсутствует
I	2-3	220	>11,0	>12	Исключитель-ное

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Нерегулярное двумерное волнение

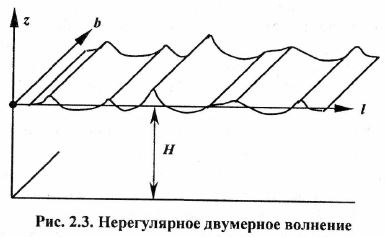
В условиях волнения следующие одна за другой волны различаются между собой по амплитуде, периоду, длине, форме, протяженности гребней, направлению распространения. Волны, характеристики которых не повторяются, являются нерегулярными. Форма профиля реальных ветровых волн близка к трохоиде, но отличается от нее более крутым подветренным и пологим наветренным склоном. Напомним, что трохоидой называется кривая, описываемая точкой, лежащей на краю или внутри круга, который катится без скольжения по прямой линии. Нерегулярность и определенная хаотичность взволнованной поверхности моря дали основание рассматривать ее как случайное поле. При решении ряда задач волнение считают изотропным однородным случайным полем (рис. 2.3), представляемым совокупностью плоских нерегулярных волн со случайными фазами. В этом случае гребни волн имеют бесконечную длину, а профили индивидуальных волн во всех параллельных линии распространения вертикальных плоскостях – одинаковы.

Предположение об изотропности волн сводит трехмерное волнение к двумерному виду. Двумерная модель нерегулярного волнения довольно широко применяется при расчетах мореходности судов. Это объясняется тем, что протяженность гребней ветровых волн в среднем в два-три раза превышает их длину. У волн зыби это отношение еще больше. Когда волнение существенно влияет на судно, гребни морских волн по длине обычно больше судна, что и позволяет приближенно считать волнение двумерным.

Изотропное нерегулярное волнение характеризуется своим сечением плоскостью, перпендикулярной гребням. Волновую ординату в точке пространства считают случайным стационарным процессом, удовлетворяющим условиям эргодичности. Вероятностные свойства нерегулярного двумерного волнения отражаются рядом показателей.

Распределение ординат и амплитуд волн. В данной точке моря волновая ордината является случайной непрерывной величиной. Такие величины полностью описываются функцией плотности распределения. На основе многочисленных экспериментальных данных установлено, что значения волновой ординаты подчиняются нормальному закону. Амплитуды и высоты волн следуют закону Релея.

Главные характеристики волнения. При решении многих практических вопросов нет надобности описывать волнение плотностью распределения. Достаточно бывает ограничиться численной характеристикой его направления и интенсивности.

Направление волнения. В отечественной практике судовождения и в ряде других стран основными являются показатели стороны волнения против бега волн: Aw или q. В других зарубежных странах ими считаются направления по бегу волн: Kw или qw, отличающиеся от первых на 180°. Поэтому,
используя различные средства для оценки мореходности, необходимо обращать внимание на вид применяемых в них характеристик направления волнения. Ниже при изложении материала используются направления волнения против бега волн (q и Aw).

Интенсивность волнения. Силу нерегулярного волнения характеризуют в баллах, средним квадратичным значением волновой ординаты, высотой волн трехпроцентной обеспеченности, высотой значительных волн. Обеспеченностью называется вероятность в процентах факта, что высота волн окажется больше заданной величины. В районах больших глубин обеспеченность определяется в соответствии с законом Релея.

Среднее квадратичное значение волновой ординаты σr представляет собой квадратный корень из дисперсии волнения, рассматриваемого как случайный стационарный процесс. Этот показатель называют также наивероятнейшей амплитудой волнения. Ее обеспеченность составляет 60,6%.

В отечественной практике, а также в России, стандартным показателем интенсивности волнения считается высота волн трехпроцентной обеспеченности – h3%. Под высотой волны 3%-ой обеспеченности понимают такую высоту, вероятность превышения которой составляет 3%. Иначе говоря, h3% – это значение, больше которого могут быть только высоты трех из 100 последовательных волн.

Высота волн с обеспеченностью 0,1% условно принимается за наибольшую возможную в данном месте моря при шторме определенной силы. Различают также среднюю высоту волн (h = 0,625/h1/3), которая имеет обеспеченность 45,6%. В ряде источников можно встретить высоты волн другой обеспеченности, чем рассмотрены выше, например: 1% 2% 5%, 10%, 20%.

Корреляционная Функция волнения. Для описания вероятностных свойств изменения волновой ординаты во времени используется корреляционная функция Кг(т). В простейшем случае ее представляют выражением.

Здесь τ– разность моментов времени; σr – среднее квадратичное значение волновой ординаты; ωp – частота преобладающей гармоники волновой ординаты (гармоника, которая несет наибольшую энергию); cp – коэффициент затухания. Частота преобладающей гармоники волновой ординаты – это пиковая частота, соответствующая максимуму спектра волнения. Как показал Н.Н.Рахманин, для развитого волнения на глубокой воде приближенно можно считать.

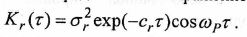
Спектр волнения. По рассмотренным выше характеристикам морского волнения затруднительно находить показатели мореходности судна. Гораздо проще это выполняется при замене волновой ординаты как функции времени случайной функцией вспомогательной комплексной переменной, имеющей размерность частоты.

При переходе к частотной координате нерегулярное волнение рассматривается как результат наложения неограниченного числа плоских гармонических волн со случайными амплитудами, частотами и фазами. Для судна, принимаемого за линейную динамическую систему, это позволяет представлять его реакцию на морское волнение в виде суммы реакций на гармонические волны. В результате исследование влияния нерегулярного волнения на судно сводится к простым методам, которые применяются при изучении действия на него регулярного волнения.

Для частотной характеристики плоского нерегулярного волнения как случайного стационарного процесса используется функция спектральной плотности волновых ординат Sr (со) (энергетический спектр), представляющая распределение энергии волнения по различным частотам. Эту функцию также называют одномерным волновым спектром. Переход от временной к комплексно-частотной области с использованием спектральных характеристик позволяет значительно упростить выкладки при определении параметров качки по данным о волнении. Этот способ нашел широкое применение при расчетах мореходности.

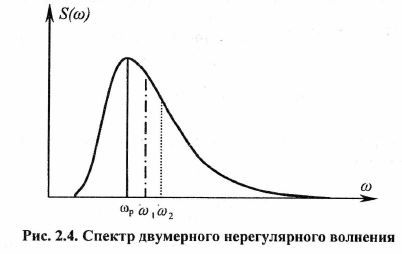
Функцию спектральной плотности волновых ординат в общем случае можно представить графиком, изображенным на рис. 2.4. Гармонику, соответствующую максимуму спектра, называют преобладающей.

Спектр волнения связан с корреляционной функцией этого процесса выражением.

Как всякое распределение, спектральная плотность может быть охарактеризована интегральными параметрами моментами.

Спектральным моментом случайной функции со спектром Sr (ω) называется величина:

Число j называется порядком момента. Оно может принимать любое целое положительное значение.
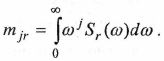
Через спектральные моменты выражаются характеристики, отражающие основные свойства волнения.
Дисперсия волновой ординаты. Момент нулевого порядка равен площади, ограниченной спектральной кривой. Он пропорционален полной энергии волнения и равен дисперсии 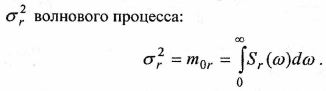Дисперсии скорости и ускорения волновой ординаты. Известно, когда случайный стационарный процесс имеет производную, то для получения ее частотного распределения

Идеализированные спектры морского волнения. Форма волнового спектра в данном месте и в данное время является неповторимой. Она зависит от текущих значений гидрометеорологических параметров, предыстории их изменения, географических и океанографических особенностей акватории. При практических расчетах, связанных с учетом волнения, для описания спектральной плотности волновых ординат используются предложенные рядом авторов функции. Они называются идеализированными волновыми спектрами, так как отражают только общие черты, присущие волнению всех морских глубоководных акваторий. По числу параметров, определяющих эти функции, спектры волнения бывают одно, двух и много параметрическими.

Для расчета спектров первого вида достаточно знать только один параметр – высоту волн. Для определения двухпараметрических спектров требуется знать высоту и средний период волнения. Из известных описаний распределения энергии ветрового волнения можно назвать спектры Ю.М.Крылова, А.И.Вознесенского-Ю.А.Нецветаева, Г.А.Фирсова, Пирсона-Московица, Неймана, Бретшнайдера, Хассельмана (спектр JONS W АР). Касаясь последнего распределения, следует отметить, что в 1968 и в 1969 году выполнялась обширная программа по измерению параметров ветрового волнения в Северном море, известная как JONSWAP (Joint North Sea Wave Project). На основе анализа ее результатов было получено выражение волнового спектра, названного по имени этой программы – JONSWAP. На 15-ой Международной конференции опытовых бассейнов (ITTC – International Towing Tank Conference) в 1978 году этот спектр был принят в качестве стандартного для Северного моря.

Большинство идеализированных спектров волнения относится к частотным распределениям, описываемых моделью:

где А, В,K,n– параметры, зависящие от статистических характеристик волнения и условий волнообразования.

Спектр смешанного волнения. Реальное волнение чаще всего является смешанным и состоит из ветровых волн и зыби. Энергетический спектр смешанного волнения существенно отличается от рассмотренных выше идеализированных частотных распределений ветровых волн. Он, как правило, имеет два максимума, которые приближенно соответствуют пикам спектров каждой из волновых систем, образующих смешанное волнение. Спектр зыби обычно расположен в области более низких частот, чем спектр ветровых волн. Для возможности учета особенностей двух систем волнения при решении практических задач Гидрометцентры в настоящее время передают прогнозы, как основных параметров смешанного волнения, так и его составляющих (ветрового волнения и зыби).

В современном программном обеспечении для расчета реакции судна на волнение используется обычно два волновых спектра – спектр ветрового волнения и спектр зыби. Реакция судна на смешанное волнение получается как сумма реакций на две составляющие его системы волн

Источник

Повторяемость и обеспеченность волнения.

Реальные ветро­вые волны отличаются разнообразием своих характеристик.

При различных условиях формирования волнения — скорости ветра, продолжительности его действия, разгона волн — наблю­даются волны от начинающих формироваться до максимальных.

Однако наблюдения показывают, что существуют статисти­ческие закономерности в разнообразии характеристик волн.

Простейший статистический анализ разнообразия волн состоит в определении повторяемости и обеспеченности элементов волн в точке при определенных параметрах ветра, а также в заданном районе за длительные промежутки времени.

Повторяемость волнения — вероятность появления волны определенных размеров (высота, длина, период) из обще­го числа наблюдений.

Обеспеченность волнения характеризует распределе­ние элементов волн по размерам из общего числа наблюдений. Для расчета обеспеченности последовательно суммируют повто­ряемости, начиная с повторяемости наибольших значений эле­ментов. На рис. 53 приведены кривые повторяемости и обеспечен­ности высот волн в безразмерной форме, отнесенные к средней вы­соте волны.

Использование относительных величин элементов волн позво­ляет сравнивать характеристи­ки, полученные при различных наблюдениях.

Кривая повторяемости вы­сот волн позволяет установить ряд закономерностей в их рас­пределении, характерных для ветрового волнения. Например, как видно из рис. 53, большин­ство наблюдающихся волн име­ет высоты около 0,8 высоты средней волны. Повторяемость волн как с большей, так и с меньшей высотой быстро умень­шается. Повторяемость длин волн характеризуется теми же значениями, что и повторяе­мость высот. Разнообразие волн по периодам значительно мень-

/ — повторяемости; 2 — обеспеченности ПерИОДОМ.

Обеспеченность средней высоты волн составляет 46 %, т. е. только это количество волн имеет высоту выше средней. Обеспе­ченность волн высотой 2h равна примерно 5 %, следовательно, только пять волн из 100 будут иметь высоту 2h и более.

Расчет обеспеченности периодов показывает, что максималь­ный период волн превышает средний не более чем в два раза. Обеспеченность среднего периода близка к 50 %.

Следует отметить, что в большинстве навигационных гидро­метеорологических пособий приводятся волны 3 %-ной обеспечен­ности. Следовательно, если на карте нанесены изолинии волн высотой 5 м, то это следует читать так: три волны из ста имеют высоту 5 м и более.

Для практических задач судовождения используется много­летняя повторяемость волнения той или иной высоты в определен­ном районе океана на различные месяцы или сезоны года.

В табл. 14 дана повторяемость высот волн в наиболее штор­мовых зонах Мирового океана (в %).

Из табл. 14 видно, что наибольшая повторяемость штормовых волн высотой 6 м и более наблюдается летом и зимой в южных частях Индийского и Тихого океанов. В северных и южных частях Атлантического океана и северной части Тихого океана в летнее время волнение высотой 6 м и более практически не встречается.

Отдельные волны в зоне сильного шторма могут достигать значительно больших размеров, чем их средние значения. Так в Северной Атлантике при ветре 20 м/с наблюдались волны высо­той 15—20 м.

Статистический анализ элементов волн позволяет определить, помимо повторяемости и обеспеченности волнения, эмпирические 125

зависимости между скоростью ветра и (м/с), продолжительно­стью его действия t (ч), длиной разгона X (км) и средними значе­ниями элементов волн, числовые значения которых даны в «Океа­нографических таблицах».

Статистические связи часто представляют в виде номограмм, удобных для практического расчета. На рис. 54 показана подоб­ная номограмма для нахождения средней высоты волны по из­вестным значениям среднего периода и скорости ветра. Аналити-

честв судов на волнении используются спектральные характе­ристики ветрового волнения.

Спектральный метод рассматривает процесс волновых коле­баний как сложную, не повторяющуюся в деталях кривую, кото­рую можно представить в виде суммы элементарных синусоидаль­ных колебаний с различными амплитудами а, частотами ю = (где т — период волны) и случайными фазами є:

Ч = I

где Г|(?) — отклонение ординаты взволнованной поверхности от среднего волнового уровня в момент времени t в фиксированной точке моря.

В силу случайности фаз эта величина носит вероятностный, случайный характер.

Энергия элементарного колебания е„ пропорциональна квадра­ту амплитуды волны а„ и определяется формулой

где р — плотность морской воды, кг/м 3 ;

Реальная кривая колебаний поверхности моря состоит из мно­жества составляющих с интервалом частот бесконечно малым Ato^>0. В этом случае распределение энергии волны по частотам определяется кривой спектральной плотности.

Рис. 54. Номограмгиа для нахождения средней высоты волны по известным значениям среднего периода и скорости ветра

Спектральная плотность энергии есть размерный коэффициент, на который нужно умножить бесконечно малый интервал частот dw, чтобы найти величину энергии элементарных составляющих с частотами от ш до to + dw:

вается спектром сложного колебательного процесса.

Суммарная энергия реальной волны Е будет определяться интегралом (суммой) энергий элементарных волн во всем диа­пазоне частот от 0 до со, т. е. интегралом вида

Как показывают натурные наблюдения, волновая энергия распространяется не только в направлении ветра, но и в других направлениях.

Поэтому взволнованную поверхность моря следует рассмат­ривать как сумму бесконечного множества составляющих не только с различными частотами ю но и с различными направлениями распространения 0°.

Теория объясняет лишь некоторые частные свойства дву­мерного энергетического спектра, но не позволяет вычислить его по заданным параметрам ветрового потока. Поэтому приходит­ся определять значения энергетических спектров эмпирическим пу­тем.

В общем случае они имеют следующий вид:

Рис. 55. Кривая спектральной плотнос­ти для неустановившегося и установив­шегося волнения при скорости ветра и=12 м/с, 1—1 = 3 ч; 2—t=

Источник