Возможно ли что область определения функции y sin10x x
Область определения функции
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.
Разложим квадратный трёхчлен на множители:
Дискриминант положительный. Ищем корни:
Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Область определения степенной функции
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
Рассмотрим несколько примеров.
Область определения показательной функции
Область определения показательной функции — это множество R.
Примеры показательных функций:
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
Область определения этих функций есть множество (0, +∞).
Пример
Укажите, какова область определения функции:
Составим и решим систему:
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Область определения функции
Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.
Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма. Областью определения показательной функции, также как и у постоянной функции, является множество всех действительных чисел.
Областью определения сложных функций y=f1(f2(x)) является пересечение двух множеств: x∈D(f2) и множества всех x, для которых f2(x) ∈ D(f1). Следовательно, для того чтобы найти область определения сложной функции, необходимо решить систему неравенства.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать и понимать, как находить область определения функции. Чтобы получить ответ, укажите функцию, для которой Вы хотите найти область определения. Основные примеры ввода функций и переменных для данного калькулятора указаны ниже.
Примеры функций: sqrt(16-ln(x^2))/sin(x)) или (5x^7+4x^6-3)/((3+2x-x^2)x^4)
Построение графиков функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
Функция y = sin x, её свойства и график
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).
Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.
п.2. Свойства функции y=sinx
2. Функция ограничена сверху и снизу
Область значений \(y\in[-1;1]\)
3. Функция нечётная
4. Функция периодическая с периодом 2π
5. Максимальные значения \(y_
Минимальные значения \(y_
Нули функции \(y_<0>=sinx_0=0\) достигаются в точках \(x_0=\pi k\)
6. Функция возрастает на отрезках
Функция убывает на отрезках
7. Функция непрерывна.
п.3. Примеры
Пример 2. Решите уравнение графически:
a) \(sinx=3x\)
Один корень: x = 0
б) \(sinx=2x-2\pi\)
Один корень: x = π
в) \(sinx-\sqrt
\(sinx=\sqrt
Один корень: x = π
14. Свойства функций синуса, косинуса, тангенса
и котангенса и их графики
14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК
График функции y = sin x (синусоида)

Свойства функции y = sin x

Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:
1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями
координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее
З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох
(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордина-
та соответствующей точки единичной окружности
(рис. 79). Поскольку ординату можно найти для
любой точки единичной окружности (в силу того,
что через любую точку окружности всегда можно
провести единственную прямую, перпендикуляр-
ную оси ординат), то область определения функции
y = sin x — все действительные числа. Это можно за-
писать так: D (sin x) = R.
Для точек единичной окружности ординаты нахо-
дятся в промежутке [–1; 1] и принимают все значения
от –1 до 1, поскольку через любую точку отрезка [–1; 1]
оси ординат (который является диаметром единичной
окружности) всегда можно провести прямую, перпендикулярную оси орди-
нат, и получить точку окружности, которая имеет рассматриваемую орди-
нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].
Это можно записать так: E (sin x) = [–1; 1].
Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции sin x равно минус единице. Это значение
достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть
при
поэтому ее график симметричен относительно начала координат.
В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом
k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых sin x, то есть ордината соответствующей точки единичной окруж
ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж-
ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).
функции синус положительны (то есть ордината соответствующей точки
единичной окружности положительна) в I и II четвертях (рис. 80). Таким
образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех
x ∈ (2πk; π + 2πk), k ∈ Z.
Значения функции синус отрицательны (то есть ордината соответствую-
щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-
Промежутки возрастания и убывания
Учитывая периодичность функции sin x с периодом T = 2π, достаточно
исследовать ее на возрастание и убывание на любом промежутке длиной
2π, например на промежутке
то при увеличении аргумента x (x 2 > x 1 ) ордината соответствующей точки единичной окружности увеличивается (то есть
sin x 2 > sin x 1 ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,
делаем вывод, что она такж е возрастает на каждом из промежутков
Если x ∈ 
окружности уменьшается (то есть sin x 2 1 ), таким образом, на этом промежутке функция sin x убывает. Учитывая
периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой
функции (с периодом 2π), д о статочно сначала построить график на любом промежутке длиной 2π, на пример на
промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината
соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на
промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для
построения графика на промежутке [–π; 0] отображаем полученную кривую симметрич но относительно начала координат
Поскольку мы построили график на
промежутке длиной 2π, то, учитывая
периодичность синуса (с периодом 2π),
повторяем вид графика на каждом про-
межутке длиной 2π (то есть переносим па-
раллельно график вдоль оси Ох на 2πk,
где k — целое число).
Получаем график, который называется
З а м е ч а н и е. Тригонометрические функции широко применяются в ма тематике, физике и технике. Например,
множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,
описываются функцией, которая задается формулой y = A sin (ωх + φ). Та кие процессы называют гармоническими
колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль
координатных осей и параллельным пере носом вдоль оси Ох. Чаще всего гармоническое колебание является функцией
времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная
фаза,
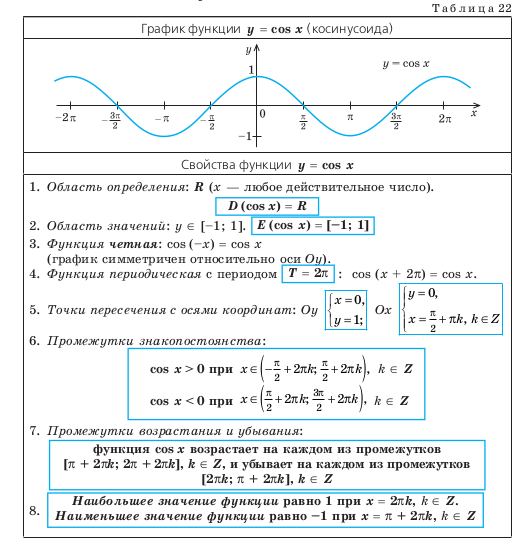
14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК
Объяснение и обоснование
Напомним, что значение косинуса — это абсцис-
са соответствующей точки единичной окружности
(рис. 85). Поскольку абсциссу можно найти для лю-
бой точки единичной окружности (в силу того, что
через любую точку окружности, всегда можно про-
вести единственную прямую, перпендикулярную оси
абсцисс), то область определения функции y = cos x —
все действительные числа. Это можно записать так:
D (cos x) = R.
Для точек единичной окружности абсциссы нахо-
дятся в промежутке [–1; 1] и принимают все значе-
ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной
всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следователь но, область значений функции y = cos x:
y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1]. Как видим, наибольшее значение функции cos x равно единице. Это
зна чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окруж ности является точка B, то есть при x = π + 2πk, k ∈ Z.
Как было показано в § 13, косинус — четная функция : cos (–x) = cos x, поэтому ее график симметричен относительно оси
Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом
T = 2π: cos (x + 2π) = cos x. Таким об разом, через промежутки длиной 2π вид графика функции cos x повторяется.
соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только
тогда, когда на единичной окружности будут выбраны точки C или D, то есть при
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции косинус положительны (то есть абсцисса соответствующей точки
единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-
тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех
Значения функции косинус отрицательны (то есть абсцисса соответству-
ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,
поэтому cos x
Промежутки возрастания и убывания
Учитывая периодичность функции cos x (T = 2π), достаточно исследовать
ее на возрастание и убывание на любом промежутке длиной 2π, например
на промежутке [0; 2π].
Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x 2 > x 1 ) абсцисса соответствующей точки единичной
окружности уменьшается (то есть cos x 2 1 ), следовательно, на этом промежутке функция cos x убывает. Учитывая
периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.
Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x 2 > x 1 ) аб-
сцисса соответствующей точки единичной окружности увеличивается (то
есть cos x 2 >cos x 1 ), таким образом, на этом промежутке функция cos x
возрастает. Учитывая периодичность функции cos x, делаем вывод, что
она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.
Проведенное исследование позволяет построить график функции y = cos x
аналогично тому, как был построен график функ-
ции y = sin x. Но график функции у = cos x можно
также получить с помощью геометрических преоб-
разований графика функции у = sin х, используя
Эту формулу можно обосновать, например, так.
Рассмотрим единичную окружность (рис. 88), отметим на ней точки