Вписанный угол что это

Вписанные и центральные углы, их свойства

теория по математике 📈 планиметрия

Вписанный угол

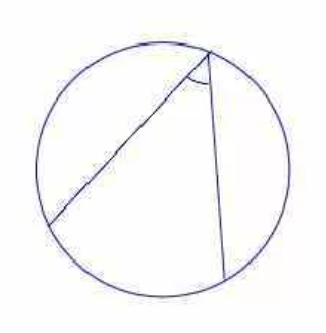
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Свойства вписанных углов

Вписанный угол равен половине дуги, на которую он опирается.

Свойство вписанного угла №2

Вписанные углы, которые опираются на одну и ту же дугу, равны.

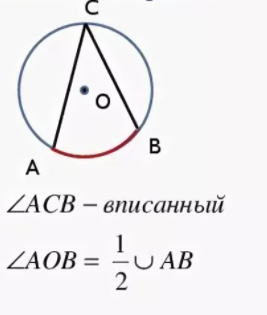
На рисунке показаны три вписанных угла – ACD, AFD, AND, которые опираются на одну и ту же дугу AD, поэтому эти углы равны.

Свойство вписанного угла №2

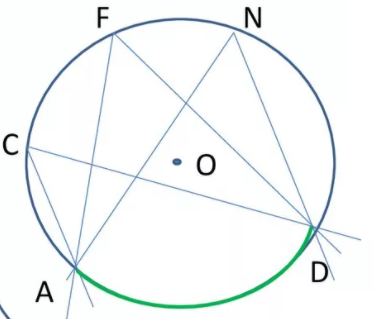
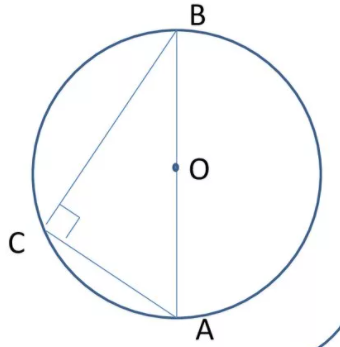
Вписанный угол, который опирается на диаметр, прямой.

Центральный угол

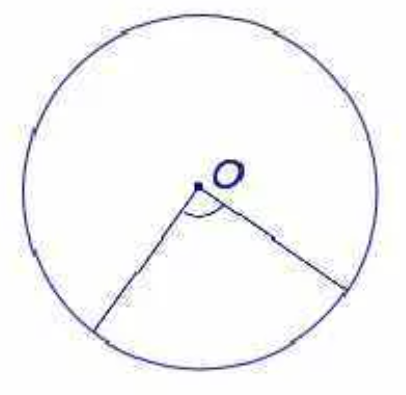
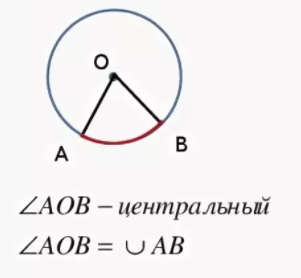
Центральный угол – это угол, вершина которого лежит в центре окружности.

Свойства центральных углов

Центральный угол равен дуге, на которую он опирается.

Свойства вписанного и центрального угла

Если центральный и вписанный угол опираются на одну и ту же дугу, то вписанный угол равен половине центрального угла. И наоборот, центральный угол в 2 раза больше вписанного, если они опираются на одну и ту же дугу.

Источник

Углы, связанные с окружностью

Вписанные и центральные углы

Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

Теоремы о вписанных и центральных углах

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу равны.

Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Теоремы об углах, образованных хордами, касательными и секущими

Фигура	Рисунок	Теорема
Вписанный угол

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами
Угол, образованный секущими, которые пересекаются вне круга
Угол, образованный касательной и хордой, проходящей через точку касания
Угол, образованный касательной и секущей
Угол, образованный двумя касательными к окружности

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Доказательства теорем об углах, связанных с окружностью

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

что и требовалось доказать.

что и требовалось доказать.

что и требовалось доказать

что и требовалось доказать.

Источник

Вписанный и центральный угол окружности (ЕГЭ 2022)

С появлением окружности, а затем колеса человечество сильно упростило себе жизнь.

И через много веков на ЕГЭ появились задачи по этой теме, конечно же 🙂

Зная свойства вписанного и центрального угла окружности, ты сможешь решить множество таких задач. И в этой статье мы тебе с этим поможем.

Вписанный и центральный угол окружности — коротко о главном

Центр окружности – такая точка, расстояния от которой до всех точек окружности одинаковые.

Радиус – отрезок, соединяющий центр и точку на окружности.

Радиусов очень много (столько же, сколько и точек на окружности), но длина у всех радиусов – одинаковая.

Иногда для краткости радиусом называют именно длину отрезка «центр – точка на окружности», а не сам отрезок.

А вот что получится, если соединить две точки на окружности? Тоже отрезок? Так вот, этот отрезок называется «хорда».

Тут есть ещё одно принятое выражение: «хорда стягивает дугу». Вот, здесь на рисунке, например, хорда \( \displaystyle AB\) стягивает дугу \( \displaystyle AB\).

А если хорда вдруг проходит через центр, то у неё есть специальное название: «диаметр».

Так же, как и в случае с радиусом, диаметром часто называют длину отрезка, соединяющего две точки на окружности и проходящего через центр. Кстати, а как связаны диаметр и радиус? Посмотри внимательно. Конечно же,

Радиус равен половине диаметра.

Кроме хорд бывают еще и секущие.

Вспомнили самое простое?

А теперь – названия для углов.

Центральный угол – угол между двумя радиусами.

Естественно, не правда ли? Стороны угла выходят из центра – значит, угол – центральный.

А теперь – вписанный угол.

Вписанный угол – угол между двумя хордами, которые пересекаются в точке на окружности.

При этом говорят, что вписанный угол \( \displaystyle ABC\) опирается на дугу (или на хорду) \( \displaystyle AC\).

Вот здесь иногда возникают сложности. Обрати внимание – НЕ ЛЮБОЙ угол внутри окружности – вписанный, а только такой, у которого вершина «сидит» на самой окружности.

Смотри на картинку:

Измерение дуг и углов окружности

Длина окружности. Дуги и углы измеряются в градусах и радианах.

Сперва о градусах

Для углов проблем нет – нужно научиться измерять дугу в градусах.

Градусная мера (величина дуги) – это величина (в градусах) соответствующего центрального угла

Что здесь значит слово «соответствующего»? Смотрим внимательно:

Видишь две дуги \( \displaystyle AB\) и два центральных угла?

Ну вот, большей дуге соответствует больший угол (и ничего страшного, что он больше \( \displaystyle 180<>^\circ \)), а меньшей дуге соответствует меньший угол.

Итак, договорились: в дуге содержится столько же градусов, сколько в соответствующем центральном угле.

А теперь о радианах

Что же это за зверь такой «радиан»?

Представь себе: радианы – это способ измерения угла … в радиусах!

Угол величиной \( \displaystyle 1\) радиан – такой центральный угол, длина дуги которого равна радиусу окружности.

Тогда возникает вопрос – а сколько же радиан в развёрнутом угле?

Иными словами: сколько радиусов «помещается» в половине окружности? Или ещё по-другому: во сколько раз длина половины окружности больше радиуса?

Этим вопросом задавались учёные ещё в Древней Греции.

И вот, после долгих поисков они обнаружили, что отношение длины окружности к радиусу никак не хочет выражаться «человеческими» числами вроде \( \displaystyle 1,\text< >2,\text< >3,\frac<7><5>,\frac<2><239>\) и т.п.

И даже не получается выразить это отношение через корни. То есть, оказывается, нельзя сказать, что половина окружности в \( \displaystyle 2,5\) раза или в \( \displaystyle \sqrt<17>\) раз больше радиуса!

Представляешь, как удивительно это было обнаружить людям впервые?! Для отношения длины половины окружности к радиусу на хватило «нормальных» чисел. Пришлось вводить букву \( \displaystyle \pi \).

Итак, \( \displaystyle \pi \) – это число, выражающее отношение длины полуокружности к радиусу.

Теперь мы можем ответить на вопрос: сколько радиан в развёрнутом угле? В нём \( \displaystyle \pi \) радиан. Именно оттого, что половина окружности в \( \displaystyle \pi \) раз больше радиуса.

Древние (и не очень) люди на протяжении веков (!) попытались поточнее подсчитать это загадочное число \( \displaystyle \pi \), получше выразить его (хоть приблизительно) через «обыкновенные» числа. А мы сейчас до невозможности ленивы – нам достаточно двух знаков после занятой, мы привыкли, что

\( \displaystyle \pi \approx 3,14\)

Задумайся, это значит, например, что y окружности с радиусом единица длина приблизительно равна \( \displaystyle 6,28\), а точно эту длину просто невозможно записать «человеческим» числом – нужна буква \( \displaystyle \pi \).

И тогда эта длина окружности окажется равной \( \displaystyle 2\pi \). И конечно, длина окружности радиуса \( \displaystyle R\) равна \( \displaystyle 2\pi R\).

Вернёмся к радианам.

Мы выяснили уже, что в развёрнутом угле содержится \( \displaystyle \pi \) радиан.

Исходя из этого, можно пересчитать любые углы «в градусах» на углы «в радианах». Для этого нужно просто решить пропорцию! Давай попробуем. Возьмём угол в \( \displaystyle 30<>^\circ \).

Значит, \( \displaystyle x=\frac<30<>^\circ \text< >\!\!\pi\!\!\text< >><180<>^\circ >=\frac<\text< >\!\!\pi\!\!\text< >><6>\)рад., то есть \( \displaystyle 30<>^\circ =\frac<\pi ><6>\)рад. Таким же образом получается табличка с наиболее популярными углами.

Угол, образованный пересекающимися хордами хордами

Формула:

Итак, осознай и не бойся: если ты видишь букву или выражение \( \displaystyle \frac<7\pi ><2>\) и т.п., то речь идёт об угле и, по сути, запись через букву \( \displaystyle \pi\) всегда выражает, какую часть от развёрнутого угла составляет тот угол, о котором идёт речь.

А для убедительности ещё раз взгляни на табличку:

Вписанный угол вдвое меньше центрального — доказательство

Имеет место удивительный факт:

Величина вписанного угла вдвое меньше, чем величина соответствующего центрального угла.

Посмотри, как это утверждение выглядит на картинке. «Соответствующий» центральный угол такой, у которого концы совпадают с концами вписанного угла, а вершина в центре.

И при этом «соответствующий» центральный угол должен «смотреть» на ту же хорду (\( \displaystyle AC\)), что и вписанный угол.

Почему же так? Почему вписанный угол вдвое меньше центрального?

Давай разберёмся сначала на простом случае.

Случай 1. Хорда проходит через центр окружности

Пусть одна из хорд проходит через центр. Ведь бывает же так иногда, верно?

Что же тут получается? Рассмотрим \( \displaystyle \Delta AOB\). Он равнобедренный – ведь \( \displaystyle AO\) и \( \displaystyle OB\) – радиусы. Значит, \( \displaystyle \angle A=\angle B\) (обозначили их \( \displaystyle \alpha \)).

Теперь посмотрим на \( \displaystyle \angle AOC\). Это же внешний угол для \( \displaystyle \Delta AOB\)!

Источник

Угол. Вписанный угол.

Вписанный угол – это угол, сформированный двумя хордами, берущими начало в одной точки окружности. О вписанном угле говорят, что он опирается на дугу, заключенную между его сторонами.

Вписанный угол равен половине дуги, на которую он опирается.

Говоря другими словами, вписанный угол включает в себе столько угловых градусов, минут и секунд, сколько дуговых градусов, минут и секунд заключено в половине дуги, на которую он опирается. Для обоснования проанализируем три случая:

Центр O расположен между сторонами вписанного угла ABС.Начертив диаметр BD, мы поделим угол ABС на два угла, из которых, по установленному в первом случае, один измеряется половиной дуги AD, а другой половиной дуги СD. И соответственно угол ABС измеряется (AD+DС) /2, т.е. 1 /₂ AC.

Следствие 1. Любые вписанные углы, опирающиеся на одну и ту же дугу одинаковы, то есть равны между собой. Поскольку каждый из них измеряется половиной одной и той же дуги.

Источник

Центральные и вписанные углы

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, что и вписанный угол.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

Угол AOC и угол ABC, вписанный в окружность, опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Хорда — отрезок, соединяющий две точки на окружности.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Как решаем: окружность 360° − ⌒AC − ⌒CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ ⌒AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ ⌒AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

⌒СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от ⌒CB = 72° / 2 = 36°

Источник