Вращение волчка что где когда
История волчка из «Что?Где?Когда?»
Что? Где? Когда? Вопросы о времени, на которые вы наверняка знаете ответ!
За 46 лет существования легендарной интеллектуальной игры «Что? Где? Когда?» знатокам было задано немало интересных вопросов, в том числе и о времени! В честь Дня рождения, которое телеигра отпраздновала 4 сентября, предлагаем вспомнить интересные загадки о часах и попробовать на них ответить.
Знатоки, внимание: вопрос!
Для разогрева обратимся к детской загадке, которую, к сожалению, не смог разгадать известный знаток и магистр игры Александр Друзь:
Когда она садится — они встают. Отгадайте загадку. О чем речь?
Александр Друзь предположил, что садиться может что угодно: «Например, «она садится» — это птица, а «они встают» — это перья»
Правильный ответ: Когда садится батарейка, часы встают. Это загадка о батарейке и часах.
Вопрос звучал следующим образом:
«В некоторых американских офисах есть такие часы. На что они указывают?»
Знатоки не справились с этим вопросом.
Правильный ответ: Часы указывают время окончания обеденного перерыва.
Похожий вопрос, но уже о бельгийских часах:
«20 лет назад в Бельгии создали такие часы. Для чего они использовались?»
Ответ знатоков был следующим: «Такие часы придумали для того, чтобы как-то правильно определять. Это связано с производством шоколада. В Бельгии очень вкусный шоколад, и, допустим, эти часы показывают что-то, связанное с шоколадом».
Правильный ответ: «Вместо единицы — 40,3, вместо двойки — 80,6, и так далее. А что было 20 лет назад не только в Бельгии, а и вообще во всей Европе? Эти часы были выпущены для того, чтобы бельгийцам было проще переводить бельгийские франки в евро, которые вошли в обращение, когда в Европе начался переход на единую валюту.»
Лучшие вопросы весенней серии игр Что? Где? Когда? 2018
Добрый вечер! Предлагаю вашему вниманию подборку лучших вопросов весенней серии игр в интеллектуальной игре Что? Где? Когда? от телезрителей за 2018 год, по мнению клуба.
1. Игра 4 марта 2018. Первая игра весенней серии. Звезды КВН против телезрителей.
Раунд 6. Счет 2:3 в пользу телезрителей.
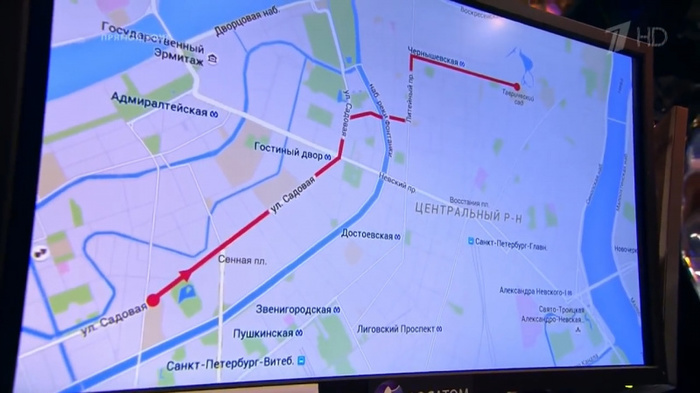
Перед вами схема одной известной вам погони. Чем закончилась эта погоня и кто в итоге расправился с преследователем?
Автор вопроса: Юлия Абрамова, г. Калининград
Правильный ответ: Это маршрут известный всем нам с детства. По Садовой по Сенной, а закончилось всё у Таврического сада.
А от бешеной мочалки
Я помчался, как от палки,
А она за мной, за мной
По Садовой, по Сенной.
Вдруг навстречу мой хороший,
Он с Тотошей и Кокошей
И мочалку, словно галку,
Словно галку, проглотил.
Знатоки не отвечают, счет становится 2:4.
2. Игра 11 марта 2018 года. Вторая игра весенней серии.
За игровым столом команда Елены Потаниной.
Раунд 8. Счет 3:4 в пользу телезрителей
Автор вопроса: Ольга Николаева, г. Химки
Правильный ответ: На зрителей сыпется огромное количество конфетти. К вечеру улицы засыпаны по щиколотку. Чтобы конфетти не собирали с земли и не использовали повторно, карнавальные комитет предписывает продавать только одноцветные конфетти. Чтобы не собирали и не продавали.
Счет становится 3:5 в пользу телезрителей.
Версия знатоков: За эти три дня город достаточно загрязняется этими конфетти. Затем каждая группа, которая бросала конфетти одного цвета, обязана убрать именно эти конфетти.
3. Игра 25 марта 2018 года. Третья игра весенней серии.
За игровым столом команда Константина Рудера.
Раунд 6. Счет 3:2 в пользу знатоков.
Автор вопроса: Надежда Дудченко, г. Днепр
Правильный ответ: Вечер в городе. Люди примерно в одно и тоже время выходят из дома и плетутся в хвосте у животных. О. Генри говорил о собачниках.
Счет становится 3:3.
Версия знатоков: Эти люди, имеющие человеческий облик не утратили способность ходить на двух ногах, но едут в экипажах следом за лошадьми. Так О. Генри говорил о людях, которые возвращаются с работы на экипажах.
4. Игра 8 апреля 2018. Четвертая игра весенней серии.
За игровым столом команда Бориса Белозерова.
Раунд 7. Счет 4:2 в пользу знатоков.
Авторы вопроса: Ольга и Владимир Шарковы, г. Красный Холм
Правильный ответ: Александр Тышлер так описал верблюда.
Счет становится 4:3
Версия знатоков: О жирафе
5. Игра 15 апреля 2018 года. Финальная игра весенней серии.
За игровым столом команда Виктора Сиднева.
Раунд 5. Счет 1:4 в пользу телезрителей.
Знатоки ответили верно, но победили в финале весенней серии телезрители со счетом 4:6.
На собачьем лае можно зарабатывать!
Многие из нас при поиске работы стараются найти что-то необычное, чтобы это было интересно и увлекательно, как в детских мечтах, где ты космонавт или знаменитый футболист или супер модель. Но вместо этого приходится довольствоваться просиживанием целыми днями в офисе или заниматься тяжелым физическим трудом.
А ведь существуют уникальные и даже странные профессии, о которых врядли кто-то мог представить себе в детстве.
Одну из таких профессий освоила Эльфрида Карлсон.
Представьте, что Вы – житель Стокгольма. Вы купили себе собаку, но не хотите платить налог на нее. Тогда налоговая посылает к Вам Эльфриду Карлсон. Эта женщина ходит по домам и гавкает на 20-ти различных ладах. И 100% собак откликаются, выдавая себя с головой, лапами и хвостом. По лаю Эльфрида определяет породу и возраст собаки, а затем выписывает счета владельцам четырехлапых..
Знатоки «Что? Где? Когда?».
В конце ХХ века игроки клуба «Что? Где? Когда?» были не менее знамениты и популярны, чем звёзды кино и эстрады. Зрители узнавали их в лицо, а многочисленные поклонники могли часами сидеть у съемочного павильона в ожидании встречи со своими кумирами. Сегодня кто-то продолжает играть теперь уже в интеллектуальном казино, а кто-то выбрал тихую спокойную жизнь вдали от блеска софитов.
Он является рекордсменом среди участников клуба, так как играет практически без перерыва, начиная с 1981 года и останавливаться не собирается. Сегодня Александр Друзь руководит отделом игровых программ на канале «СТО-ТВ» в Санкт-Петербурге, является автором и ведущим телепрограмм, в 2017 году снялся в кино (сериал «Мамочки»). Проводит тренинги по интеллектуальным играм, выступает с лекциями. Написал увлекательную книгу о Санкт-Петербурге, его памятных местах и интересных маршрутах по городу.
Один из самых ярких игроков, начиная с 1979 года. Александр Бялко получил два высших образования, первое в области ядерной физики, второе – в журналистике. Преподавал в МИФИ, занимал руководящие должности в нескольких компаниях, работал деканом одного из столичных ВУЗов, занимался научной работой. Принимал участие в программе «Последний герой», вел авторскую программу на радио. Написал пять книг и множество публицистических статей. Женившись во второй раз, стремится не привлекать внимания к себе и своей личной жизни.
Помимо «Что? Где? Когда?», у Бориса Бурды есть два серьезных увлечения: кулинария и бардовская песня. На многих фестивалях бардовской песни становился лауреатом, а любовь к кулинарии переросла в профессию. На украинском телевидении вел кулинарную передачу «Вкусно с Борисом Бурдой», которую любили не только за оригинальные рецепты, но и за интересные факты и истории, которыми щедро приправлял свою программу ведущий. По профессии Бурда инженер-теплотехник, но по призванию – талантливый кулинар. Является автором 10 книг, в основном, по кулинарии.
Активно играл в клубе 15 лет, начиная с 1990 года. Фёдор Двинятин окончил филфак СПбГУ в 1991 году, а с 1992 занимается преподавательской деятельностью. Написал около 50 научных работ и 10 книг по филологии. Не любит публичности и повышенного внимания к своей персоне. Не устает подчёркивать тот факт, что он знает на самом деле очень мало, хотя его образованность и эрудиция способны впечатлить даже самых отъявленных скептиков.
Он известен не только, как игрок «Что? Где? Когда?», но ещё и как политик, изобретатель, художник-карикатурист и писатель. Кажется, нет такой области, где Нурали Латыпов, нейрофизиолог и кандидат философских наук, был бы несведущ. Он откровенно говорит о том, что игра в клубе была для него глотком свежего воздуха, она давала ему импульсы для творчества и изобретений. Он занимал множество весьма серьёзных должностей, и сегодня руководит лабораторией и институтом. При этом продолжает рисовать карикатуры, завоёвывая Гран-при на международных конкурсах, а ещё занимается литературным творчеством, даже стал лауреатом премии «Золотой телёнок».
Он попал в клуб совершенно случайно, согласившись сопровождать стеснявшегося друга. В итоге в его активе 8 лет игр, звание лучшего капитана команды и любовь и признание зрителей. После окончания МГИМО работал журналистом-международником. Сегодня возглавляет компанию «Форвард-фильм», не отказывается от участия в юбилейных играх клуба.
В 1989 году Максим принял участие в отборе на знаменитое телешоу «Что? Где? Когда?». В 1994 году знаменитый эрудит также вошел в элитарный клуб игроков в «Что? Где? Когда?». После этого ни одна игра не была пропущена. Это был огромный успех, ведь в те времена из тысяч игроков по всему миру на телеэкраны попадали лишь единицы. Позже, Максим Поташев устроился работать начальником аналитического центра известной компании «Лаборатория Касперского» по выпуску антивирусов для программных обеспечений компьютеров.
Впервые на всесоюзном экране появился 14 октября 1989-го, в команде Нурали Латыпова, в элитарном клубе «Что? Где? Когда?», затем — в команде Виктора Мороховского на «Брейн-ринге».
Создательница и капитан первой и единственной женской команды появилась в клубе в 1982 году. Желание стать участницей было связано с личной симпатией к одному из членов интеллектуального клуба. За её плечами обучение на кафедре прикладной математики в Белорусском университете, звание кандидата технических наук и множество руководящих должностей в сфере политического консалтинга и связей с общественностью. Кроме того, Валентина Голубева ведет спецкурс в МГИМО и часто бывает в интеллектуальном казино и на играх в качестве зрителя.
Крутится волчок: викторина «Что? Где? Когда?» радует зрителей уже 46 лет
4 сентября считается официальным днем рождения интеллектуальной игры «Что? Где? Когда?». Впервые программа вышла в эфир в 1975 году, правда, тогда она сильно отличалась от той, которую мы видим на экранах сейчас.
Первый выпуск назывался «Семейной викториной», в нем согласились сыграть две московские семьи по фамилии: Ивановы и Кузнецовы. Участникам у них дома задали по 11 вопросов, а затем свели вместе обе части записи перед показом по телевидению.
Загадочный ведущий
Первые вопросы писали редакторы и 12-летний школьник Боря Крюк. Он же первый телезритель, выигравший у знатоков, не сумевших разгадать его шахматную задачку. Да, именно он — Борис Крюк — стал ведущим после смерти в 2001 году Владимира Ворошилова.
Первые пять лет эфира зрители вообще не знали кто ведет игру, слышали лишь его грозный голос. А игроки обращались к нему «Господин ведущий». Кстати, так же они обращаются и сейчас, чтя традиции. Ворошилова вообще называли «Инкогнито из Останкино», о его участии в игре не знали даже в студии.
Более трех десятков лет съемки программы проходят в Нескучном саду столицы. Павильоном служит охотничий домик князя Никиты Трубецкого, являющийся памятником архитектуры XVIII века.
Филин Фомка и хрустальная сова
Хрустальная сова, которую вручают лучшим игрокам, возникла не на пустом месте. Эту птицу считают самой мудрой обитательницей природы, а прототипом награды стал вполне реальный персонаж — филин Фомка, появившийся в эфире в 1977 году. Приз же в виде птицы впервые был вручен самому умному в 1984 году, а в 2002 появилась еще и бриллиантовая сова по итогам года.
Самый загадочный предмет на передаче — черный ящик. За долгие годы в нем побывали: туалетная бумага, свадебное платье, пух, шпоры, кирпич, мыло, дирижерская палочка, череп, купальник, баночка с мочой, будильник, живая бабочка и даже однажды самый настоящий «черный ящик» авиалайнера. Несколько раз тара пустовала, ставя игроков в тупик.
Детская игрушка и деньги за сообразительность
Доподлинно неизвестно, у кого возникла идея запустить в игре волчок со скачущей лошадкой, но это чуть усовершенствованная детская игрушка, которую до сих пор выпускает столичный завод «Красный пролетарий». Ведущий Владимир Ворошилов как-то признавался, что зашел в детский магазин что-то купить ребенку и, увидев волчок, приобрел его не только в подарок, но и себе. Игрался дней десять, получая невероятное удовольствие от лошадки, раз за разом берущей препятствия.
Изначально игра в «Что? Где? Когда?» не имела финансовой составляющей. Победители получали призы в виде книг. Денежными выигрышами их стали награждать лишь с 1991 года, когда интеллектуальный клуб переименовали в казино. Девизом стала фраза: «Интеллектуальное казино – единственное место, где можно заработать деньги своим собственным умом».
За время своего существования телевикторина «Что? Где? Когда?» семь раз награждалась премиями ТЭФИ, включая победу в номинации «Звукорежиссер». Телезрители давно заметили, что каждому действию в программе соответствует определенная музыка. Волчок крутится под композицию Геннадия Бондарева «Дикая лошадь», появление черного ящика происходит под «Ra-Ta-Ta» Криса Ювенса и Кристиана Хайльбурга, а хрустальная сова обретает хозяина под аккомпанемент Homage To The Mountain группы Yello.
Китайский волчок: теория переворота!

. однозначного ответа. Считаю, что, отчасти, это мнение – миф, и попытаюсь его слегка развеять.
Китайский волчок, он же волчок Томсона, он же волчок «тип-топ» представляет собой шарик со срезанным шаровым сегментом высотой около или чуть больше половины радиуса сферы. К плоскости среза присоединена цилиндрическая ручка, которая выступает за сферическую поверхность шарика. При сообщении китайскому волчку вращательного импульса (кинетического момента) вокруг оси, проходящей через центр шарика и совпадающей с осью цилиндрической ручки, направленной вначале вертикально вверх, он, достаточно быстро приподнимаясь, переворачивается на 180°, приподнимается на торец ручки и в этом положении, опираясь на свою шейку, направленную теперь вертикально вниз, продолжает устойчивое вращение. Это вращение на торце ручки длится до момента, пока сила трения не «победит» кинетический момент, и кинетическая энергия не перейдет в тепловую энергию. В этом состоит суть явления.
Посмотрите видео с китайским волчком, их на «You Tube» много. Например: https://www.youtube.com/watch?feature=player_embedded&v =bp2yKEjA8V4
Попробуем разобраться — как происходит переворот волчка, какая «магическая сила» заставляет китайский волчок перевернуться, подняв вверх свой центр тяжести и продолжать вращение в, казалось бы, очень неустойчивом положении.
Общие исходные сведения
1. Неподвижная система координат Ox0y0z0 изображена на рисунках лиловым цветом. Центром этой прямоугольной системы координат является точка O, являющаяся геометрическим центром шарика (центром кривизны сферической наружной поверхности).
2. Подвижная система координат Oxyz показана на рисунках синим цветом. Оси этой системы участвуют во всех движениях волчка. Чтобы было понятнее, можно сказать, что оси x, y, z – это спицы, проткнувшие твердое тело волчка. Ось z всегда жестко связана (совпадает) с прямой, проведенной через точки O и C. Точка C – это центр тяжести волчка, который в начальный момент расположен ниже центра кривизны опорной поверхности точки O. Ось y всегда находится в плоскости действия векторов внешних сил – силы тяжести G, силы инерции F и силы реакции опоры P.
4. Волчок имеет массу m и вес G=m*g, где g – ускорение свободного падения.
Китайский волчок в процессе переворота
1. Волчок в состоянии покоя находится в устойчивом положении, касаясь опорной поверхности точкой К1. Если приглядеться к нему внимательней, то мы узнаем знакомую с детства игрушку «ванька-встанька» (рис.1).
2. Запустим волчок, придав ему вращение вокруг оси z против часовой стрелки, если смотреть сверху.
3. Китайский волчок вращается не на острой ножке, как обычный классический волчок, а на шаровой поверхности с радиусом R. Поэтому из-за малейшего отклонения оси z от вертикали z0 волчок, вращающийся вокруг оси z с угловой скоростью ωотн, сразу же начинает осью своей симметрии z описывать вокруг вертикали z0 конус с незначительным углом α и вершиной в центре радиуса кривизны опорной поверхности шарика точке О (рис.2).
4. Запустить волчок без отклонения невозможно, минимальное (микронное) отклонение будет на практике всегда из-за трения в точке (точнее – пятне) К1, из-за трения об воздух, из-за неоднородности материала волчка и – как следствие — небольшого смещения центра масс C от геометрической оси симметрии z.
5. При возникновении даже малого угла рассогласования α центр тяжести волчка C тут же сместится относительно вертикали z0 на расстояние r.
6. Это смещение мгновенно вызовет возникновение центробежной силы инерции F
которая, как понятно из формулы, прямо пропорциональна массе волчка m, расстоянию смещения r центра масс точки C от вертикали z0 и квадрату абсолютной угловой скорости ω0 вокруг оси z0 , которую получил волчок при придании ему вращения.
7. Возникшая сила F и вес волчка G создают момент внешних сил M
который стремится повернуть волчок вокруг оси x (точки О) по часовой стрелке, если смотреть спереди.
8. Появление момента внешних сил рождает гироскопический эффект и прецессию. Китайский волчок начинает прецессировать! Гироскопический момент Mг пытается, противодействуя моменту внешних сил M, уравновесить его. Волчок по закону прецессии поворачивается вокруг оси y, пытаясь совместить вектор своего относительно оси z кинетического момента Hотн с вектором момента внешних сил M по самому короткому пути (то есть – вокруг оси y) (рис.2а).
9. Скорость прецессии (скорость поворота волчка вокруг оси y) ωпер вычисляется по формуле:
10. Если пренебречь трением в точке касания шариком поверхности и сопротивлением воздуха, то можно принять, что момент количества движения H0 вокруг вертикальной и неподвижной оси z0, полученный волчком при запуске, будет оставаться постоянным:
11. В связи с вышесказанным модули угловых скоростей ωотн и ωпер относительного и переносного движений будут определяться в процессе поворота, как катеты прямоугольного треугольника, подчиняясь теореме Пифагора:
12. Следовательно, при увеличении наклона оси z от вертикального положения переносная угловая скорость ωпер (скорость прецессии) будет расти, а относительная угловая скорость вращения ωотн будет падать!
13. Рост угловой скорости прецессии ωпер означает, что поворот волчка вокруг оси y будет непрерывно ускоряться, и в итоге прецессия довольно быстро «завалит» волчок в положение, когда ручка и связанная с ней ось z окажутся в горизонтальной плоскости (рис.3)!
14. В этот момент произойдет удивительная и в то же время закономерная метаморфоза! Китайский волчок прекратит на миг свое вращение вокруг оси z, он остановится. При этом он будет продолжать вращение со скоростью ω0 вокруг оси y, которая совместится с неподвижной вертикальной осью z0! На языке формул это выглядит так:
15. Длиться эта остановка будет долю мгновения. По аналогии с начальным моментом волчок, вращаясь вокруг оси z0, начнет образовывать конус с очень малым углом α при вершине точке О вследствие шарообразности опорной поверхности (рис.4). Прецессия (поворот вокруг оси y) продолжится.
16. Момент внешних сил M изменит направление своего действия и сила инерции F «возьмет в союзники» силу тяжести G для «совместной борьбы» с гироскопическим моментом Mг.
17. Гироскопический момент Mг изменит свое направление в ответ на изменение направления момента внешних сил M. Китайский волчок начнет вращение вокруг оси z в направлении противоположном своему начальному вращению.
18. Пока описанные выше моменты противодействуют друг другу, прецессия и сила трения качения сферической поверхности волчка по опорной плоскости продолжат «провоцирование опрокидывания» до момента совмещения оси z с отрицательным направлением оси z0 (рис.5).
19. Заняв вертикальное положение ручкой вниз, китайский волчок будет находиться в устойчивом положении и продолжит вращение до момента «исчерпания» кинетического момента H0 (рис.6).
20. Из-за того, что китайский волчок в отличие от классического, перекатываясь при вращении, постоянно меняет точку опоры, конец его ручки повторяет траекторию перемещения точки опоры. В период переворота эта траектория — не конус классического волчка! Если на опорную поверхность насыпать тонкий слой муки (или пудры, или талька) и запустить волчок, то после окончания вращения на поверхности шарика можно увидеть спиралевидный след (Рис.7).
Это и есть траектория перемещения точки опоры по поверхности шарика. Спиралевидный след вначале раскручивается в одну сторону (по часовой стрелке на рисунке), затем закручивается в обратную сторону.
Толкование явления профессором Смородинским
Вы поняли, что же заставляет подниматься при вращении вверх центр тяжести тела китайского волчка? Почему устойчивым для вращающегося волчка является положение с максимально поднятым центром тяжести? Быстро разобраться и понять довольно сложно…
Из существующих вариантов объяснения поведения китайского волчка мне нравится своей доходчивостью и очевидностью подход, рассказанный профессором Смородинским. Ознакомимся с ним.
1. Рассмотрим классический волчок. Сила тяжести G создает опрокидывающий момент М, а гироскопический момент Мг – удерживающий (Рис.8).
2. Примем без доказательства – как очевидный факт, что классический волчок (юла), вращаясь с большой скоростью, не падает и находится в устойчивом состоянии.
3. Попробуем доказать, что если увеличить скорость прецессии (скорость переносного вращения оси волчка) ωпер, то центр масс волчка поднимется вверх.
4. Доказательство будем вести от обратного. Предположим, что центр масс точка С опустится при увеличении скорости прецессии ωпер.
5. Но согласно рисунку тогда увеличится опрокидывающий момент М=G*r за счет увеличения плеча r силы тяжести G, а это неизбежно приведет к увеличению скорости прецессии ωпер, так как должно выполняться условие M=Mг=Hотн*ωпер. При этом кинетический момент Hотн может только немного уменьшаться в процессе вращения из-за действия сил трения.
6. Тогда согласно нашему предположению центр тяжести С должен еще сильнее опуститься, и в итоге классический волчок должен очень быстро упасть! Однако мы знаем, что этого не происходит, следовательно, сделанное предположение неверно! Центр масс С классического волчка не опускается, а поднимается с возрастанием скорости прецессии.
7. Запускаем китайский волчок, который при вращении (как мы неоднократно отмечали ранее) в отличие от классического волчка касается поверхности не одной точкой, а все время разными, перекатываясь в процессе движения по спирали на сферической поверхности основания волчка.
8. Так как в процессе переворота на волчок действует возрастающий опрокидывающий момент M при постоянно уменьшающемся кинетическом моменте Hотн (вначале до нуля в положительной области, затем, сменив направление, уменьшается в отрицательной области), то и скорость прецессии ωпер непрерывно возрастает!
9. Рост скорости прецессии ωпер вызывает подъем центра тяжести С.
10. Переворачиваясь на бок и опираясь на ручку, китайский волчок поднимает все выше и выше свой центр тяжести точку С. В перевернутом состоянии он продолжает устойчиво вращаться и ведет себя как классический волчок.
11. Осуществлению возможности переворота (перехода из неустойчивого состояния при вращении в устойчивое) способствует сферическая форма основания волчка.
Опытами более ста лет назад доказано, что вращающийся с очень большой скоростью волчок уменьшает свой вес. Какую частоту вращения необходимо задать, чтобы вес стал равным нулю или максимально приблизился к этому значению? Каким должен при этом быть материал диска волчка, чтобы его не разорвали силы инерции? Гравитация не торопится раскрывать все свои законы и секреты человеку! Самые интересные открытия ждут нас еще впереди, мы к ним подошли очень близко… Не случайно большинство работ ведущих специалистов в этой области являются закрытыми.
Подписывайтесь на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы, и не забывайте подтверждать подписку.
Подтвердить подписку необходимо кликом по ссылке в письме, которое придет к вам на указанную почту (может прийти в папку «Спам»).
Оставляйте комментарии, уважаемые коллеги! Они всегда интересны и автору и новым читателям.