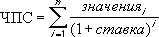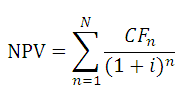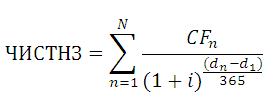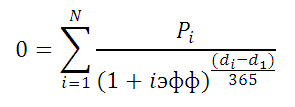Всд эксель что это такое
Работа с денежными потоками: вычисление показателей ЧПС и ВСД в Excel
Вы теряете спящий режим и знаете, как максимально повысить прибыльность и свести к минимуму риски, связанные с бизнес-инвестициями? Остановить переключение и поворот. Расслабьтесь и перейти к потоку.
Наличные, то есть. Взгляните на движение денежных средств, а также на то, что выходит за рамки вашей компании. Положительный денежный поток — это показатель получения денежных средств (продажи, проценты, проблемы с акциями и так далее), тогда как отрицательный денежный поток — это показатель выходных денежных средств (покупки, выплаты, налоги и так далее). Чистое движение денежных средств — это разница между положительным и отрицательным денежными потоками и ответы на наиболее фундаментальные деловые вопросы о том, сколько денег осталось в хлеве?
Для развития бизнеса необходимо принимать ключевые решения о том, куда вкладывать деньги в долгосрочной перспективе. Microsoft Excel сравните параметры и сделайте правильный выбор, чтобы можно было отдохнуть как днем, так и ночью.
Вопросы о проектов по capital investment
Если вы хотите взять деньги с себя, сделать его рабочим и вкладывать их в проекты, которые составляют вашу бизнес, вам нужно задать несколько вопросов об этих проектах:
Будет ли новый долгосрочный проект прибыльным? Когда?
Лучше ли вкладывать деньги в другой проект?
Следует ли вкладывать средства в текущий проект еще больше или стоит ли сократить потери?
Теперь рассмотрим каждый из этих проектов подробнее и спросите:
Каковы отрицательные и положительные денежные потоки для этого проекта?
Какое влияние оказывают крупные первоначальные инвестиции и какой объем будет слишком велик?
В итоге вам действительно нужны номера нижней строки, которые можно использовать для сравнения вариантов проектов. Но для этого необходимо включить в анализ значения времени денежных средств.
Ответы на вопросы с помощью ЧПС и IRR
Существует два финансовых способа, которые помогут вам ответить на все эти вопросы: чистая стоимость (ЧПС) и внутренняя ставка прибыли (IRR). Как ЧПС, так и IRR называются дисконтируемыми методами движения денежных средств, так как они применяют значение времени к оценке проектов по capital investment. Как ЧПС, так и IRR основаны на рядах будущих платежей (отрицательный денежный поток), доходов (положительный денежный поток), потерь (отрицательный денежный поток) или «нулевых денежных потоков».
ЧПС возвращает чистую стоимость денежных потоков, представленных в современных рублях. Из-за денежной стоимости каждый доллар сегодня стоит больше, чем завтра. ЧПС вычисляет обтекаемую стоимость для каждого ряда денежных потоков и объединяет их, чтобы получить чистую стоимость.
Где n — количество денежных потоков, а i — процентная или скидка.
IRR основан на ЧПС. Это можно представить в особом случае ЧПС, где вычисляемая ставка прибыли представляет процентную ставку, соответствующую нулевой (нулевой) чистой стоимости.
Если все отрицательные денежные потоки происходят раньше всех положительных или когда последовательность денежных потоков проекта содержит только один отрицательный денежный поток, IRR возвращает уникальное значение. Большинство проектов по инвестиции в основном начинаются с больших отрицательных денежных потоков (в начале инвестиции), за которыми следуют положительные денежные потоки, и, следовательно, имеют уникальный IRR. Однако иногда может быть несколько допустимых IRR или вообще ничего.
Сравнение проектов
ЧПС определяет, должен ли проект получить больше или меньше желаемой ставки прибыли (уровень сложности), и хорошо определяет, будет ли проект прибыльным. IRR на один шаг дальше, чем ЧПС, чтобы определить определенную ставку прибыли для проекта. Как ЧПС, так и IRR — это числа, которые можно использовать для сравнения проектов и выбора оптимальных вариантов для вашей компании.
Выбор соответствующей Excel функции
hich Office Excel функции, которые можно использовать для вычисления ЧПС и IRR? Существует пять: функция ЧПС,функция ЧПС,функция IRR,ФУНКЦИЯ XIRRи МВСД. Выбор зависит от предпочитаемого финансового метода, от того, происходят ли денежные потоки через определенные интервалы времени и являются ли они периодическими.
Примечание: Денежные потоки заданы как отрицательные, положительные или нулевые значения. При использовании этих функций обратите особое внимание на то, как вы обрабатываете мгновенные денежные потоки, которые происходят в начале первого периода, и все остальные денежные потоки, которые происходят в конце периодов.
Используйте, когда нужно
Определите чистую стоимость на основе денежных потоков, которые происходят регулярно, например ежемесячно или ежегодно.
Каждый денежный поток, заданный как значение,происходит в конце периода.
Если в начале первого периода имеется дополнительный денежный поток, он должен быть добавлен к значению, возвращаемом функцией ЧПС. См. пример 2 в разделе справки по функции ЧПС.
Определите чистую стоимость на основе денежных потоков, которые возникают через нерегулярные интервалы.
Каждый денежный поток, указанный как значение, происходит в запланированную дату платежа.
Определите внутреннюю ставку прибыли с использованием денежных потоков, которые происходят регулярно, например ежемесячно или ежегодно.
Каждый денежный поток, заданный как значение,происходит в конце периода.
Если имеется несколько допустимых ответов, функция IRR возвращает только первый из них. Если IRR не находит ответ, возвращается #NUM! значение ошибки #ЗНАЧ!. Используйте другое значение для предположения, если вы получаете ошибку или результат отличается от ожидаемого.
Примечание. Другой вариант может возвращать другой результат, если имеется более одной внутренней ставки прибыли.
ФУНКЦИЯ XIRR (значения, даты, [предположение])
Определите внутреннюю ставку прибыли с помощью денежных потоков, которые возникают через нерегулярные интервалы.
Каждый денежный поток, указанный как значение, происходит в запланированную дату платежа.
Если имеется несколько допустимых ответов, функция XIRR возвращает только первый из них. Если xiRR не находит ответ, возвращается #NUM! значение ошибки #ЗНАЧ!. Используйте другое значение для предположения, если вы получаете ошибку или результат отличается от ожидаемого.
Примечание. Другой вариант может возвращать другой результат, если имеется более одной внутренней ставки прибыли.
Функция MIRR (значения, finance_rate, reinvest_rate)
Определите модифицированную внутреннюю ставку прибыли с использованием денежных потоков, которые происходят регулярно, например ежемесячно или ежегодно, и учитывайте как стоимость инвестиций, так и проценты, полученные от реинвестирования денежных средств.
Каждый денежный поток, заданный как значение,происходит в конце периода, за исключением первого денежного потока, который определяет значение в начале периода.
Процентная ставка, которую вы платите с денежных средств, используемых в денежных потоках, указана в finance_rate. Процентная ставка, получаемая для денежных потоков при реинвестирования, указывается в reinvest_rate.
Дополнительные сведения
Внутренняя норма доходности на excel
В данной статье мы рассмотрим, что такое внутренняя норма доходности, какой экономический смысл она имеет, как и по какой формуле рассчитать внутреннюю норму доходности, рассмотрим некоторые примеры расчёта, в том числе при помощи формул MS Exel.
Оглавление
Что такое внутренняя норма доходности?
Внутренняя норма доходности (IRR — Internal Rate of Return) — один из основных критериев оценки инвестиционных проектов (доходности единицы вложенного капитала): ставка дисконта, при которой выполняется равенство суммы дисконтированных доходов по проекту (положительного денежного потока) дисконтированной сумме инвестиций (отрицательному денежному потоку, приведенному объему инвестиций), т.е. когда чистая текущая стоимость (NPV) равна нулю.
В финансово-экономической литературе довольно часто можно встретить синонимы внутренней ставки доходности:
Внутренняя норма доходности отражает как отдачу инвестированного капитала в целом, так и отдачу первоначальных инвестиций. IRR – это ставка дисконтирования, которая приравнивает сумму приведенных доходов от инвестиционного проекта к величине инвестиций, т.е. вложения окупаются, но не приносят прибыль.
Таким образом, анализ внутренней нормы доходности (прибыли) отвечает на главный вопрос инвестора: насколько ожидаемый от проекта денежный поток оправдает затраты на инвестиции в этот проект. Поэтому инвестор при оценке проектов осуществляет расчет IRR каждого проекта и сравнивает его с требуемой нормой прибыли (рентабельности), т.е. со стоимостью своего капитала.
Этот расчет обычно ведется методом проб и ошибок, путем последовательного применения к чистому денежному потоку приведенных стоимостей при различных ставках процента. Главное правило: если внутренняя норма доходности меньше требуемой инвестору ставки дохода на вложенный капитал — проект отвергается, если больше — может быть принят.
Формула расчёта внутренней нормы доходности
Внутренняя норма доходности рассчитывается по следующей формуле:
где
NPVIRR (Net Present Value) — чистая текущая стоимость, рассчитанная по ставке IRR;
CFt (Cash Flow) – денежный поток в период времени t;
IC (Invest Capital) – инвестиционные затраты на проект в первоначальном периоде (тоже являются денежным потоком CF0 = IC).
t – период времени.
или же данную формулу можно представить в виде:
Практическое применение внутренней нормы доходности
Внутренняя норма доходности применяется для оценки инвестиционной привлекательности проекта или для сопоставительного анализа с другими проектами. Для этого IRR сравнивают с эффективной ставкой дисконтирования, то есть с требуемым уровнем доходности проекта (r). За такой уровень на практике зачастую используют средневзвешенную стоимость капитала (Weight Average Cost of Capital, WACC).
| Значение IRR | Комментарии |
|---|---|
| IRR>WACC | У инвестиционного проекта внутренняя норма доходности выше чем затраты на собственный и заемный капитал, т.е. данный проект имеет инвестиционную привлекательность |
| IRR | Инвестиционный проект имеет внутреннюю норму доходности ниже чем затраты на капитал, это свидетельствует о нецелесообразности вложения в него |
| IRR=WACC | Внутренняя норма доходность проекта равна средневзвешенной стоимости капитала, т.е. данный проект находится на минимально допустимом уровне доходности, поэтому следует произвести корректировки движения денежных средств и увеличить денежные потоки |
| IRR1>IRR2 | Инвестиционный проект №1 имеет больший потенциал для вложения чем проект №2 |
Следует отметить, что вместо критерия сравнения WACC может быть использована любая другая норма доходности, например, ставка доходности по государственным облигациям, ставка по банковскому депозиту и т.п. Так, если процентная ставка по депозиту составляет 17%, а IRR инвестиционного проекта составляет 22%, то, очевидно, что деньги следует вкладывать в инвестиционный проект, а не размещать на депозит в банк.
Графический метод поиска внутренней ставки доходности
Предположим, что мы собираемся инвестировать 10 тыс. денежных единиц, и у нас есть варианты их инвестирования в 3 проекта каждый из которых, как предполагается, будет формировать определённые денежные потоки на протяжении 5 лет.
| Период, лет | Проект №1 | Проект №2 | Проект №3 |
|---|---|---|---|
| 0 | -10000 | -10000 | -10000 |
| 1 | 1000 | 1000 | 4000 |
| 2 | 4 000 | 1500 | 3000 |
| 3 | 2000 | 3000 | 2000 |
| 4 | 4000 | 4000 | 1000 |
| 5 | 2000 | 3000 | 1000 |
Продисконтируем вышеуказанные денежные потоки по 3-м проектам по разным процентным ставкам (от 0 до 14%) и на основе полученных результатов построим график.
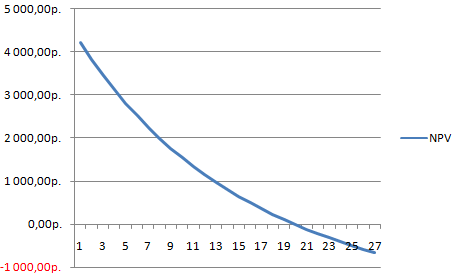
На графике прослеживается чёткая взаимосвязь между ставкой дисконтирования и чистой текущей стоимостью: чем выше ставка дисконтирования, тем ниже дисконтированная стоимость.
Внутренняя норма доходности, как это следует из определения указанного в начале данной статьи, — это тот уровень ставки дисконта, при которой NPV=0. В нашем примере внутренняя норма доходности определяется в точках пересечения кривых с осью Х. В частности, для проекта №1 IRR составляет 8,9%, для проекта №2 IRR=6,6% и для проекта №3 IRR=4,4%.
Расчёт внутренней нормы доходности (IRR) при помощи MS Exel
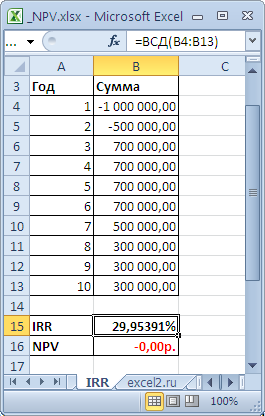
Внутреннюю норму доходности можно довольно легко рассчитать при помощи встроенной финансовой функции ВСД (IRR) в MS Exel.
Функция ВСД возвращает внутреннюю ставку доходности для ряда потоков денежных средств, представленных их численными значениями. Эти денежные потоки не обязательно должны быть равными по величине (как в случае аннуитета), однако они должны иметь место через равные промежутки времени, например ежемесячно или ежегодно. При этом в структуре денежных потоков должен обязательно быть хотя бы один отрицательный денежный поток (первоначальные инвестиции) и один положительный денежный поток (чистый доход от инвестиции).
Также для корректного расчёта внутренней нормы доходности при помощи функции ВСД важен порядок денежных потоков, т.е. если потоки денежных средств отличаются по размеру в разные периоды, то их обязательно необходимо указывать в правильной последовательности.
Синтаксис функции ВСД:
где
Значения — это массив или ссылка на ячейки, содержащие числа, для которых требуется подсчитать внутреннюю ставку доходности, учитывая требования указанные выше;
Предположение — это величина, о которой предполагается, что она близка к результату ВСД:
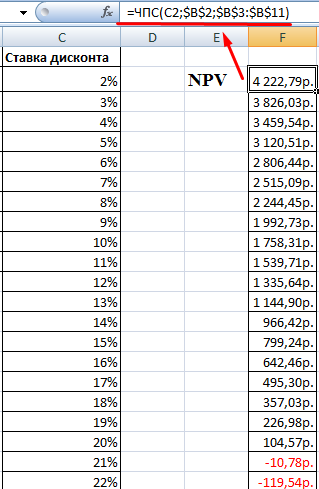
Пример расчёта внутренней ставки доходности (на основе данных о денежных потоках по трём проектам, которые рассматривались выше):
Функция ВСД в Excel и пример как посчитать IRR
Для расчета внутренней ставки доходности (внутренней нормы доходности, IRR) в Excel используется функция ВСД. Ее особенности, синтаксис, примеры рассмотрим в статье.
Особенности и синтаксис функции ВСД
Один из методов оценки инвестиционных проектов – внутренняя норма доходности. Расчет в автоматическом режиме можно произвести с помощью функции ВСД в Excel. Она находит внутреннюю ставку доходности для ряда потоков денежных средств. Финансовые показатели должны быть представлены числовыми значениями.
Суммы внутри потоков могут колебаться. Но поступления регулярные (каждый месяц, квартал или год). Это обязательное условие для корректного расчета.
Внутренняя ставка доходности (IRR, внутренняя норма доходности) – процентная ставка инвестиционного проекта, при которой приведенная стоимость денежных потоков равняется нулю. При данной ставке инвестор вернет вложенные первоначально средства. Инвестиции состоят из платежей (суммы со знаком «–») и доходов (со знаком «+»), которые происходят в одинаковые по продолжительности временные промежутки.
Аргументы функции ВСД в Excel:
Секреты работы функции ВСД (IRR):
При расчете ВСД в Excel может возникнуть ошибка #ЧИСЛО!. Почему? Используя метод итераций при расчете, функция находит результат с точностью 0,00001%. Если после 20 попыток не удается получить результат, ВСД вернет значение ошибки.
Когда функция показывает ошибку #ЧИСЛО!, повторите расчет с другим значением аргумента «Предположение».
Примеры функции ВСД в Excel
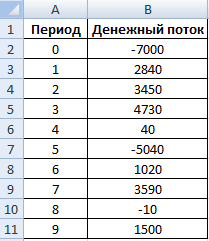
Расчет внутренней нормы рентабельности рассмотрим на элементарном примере. Имеются следующие входные данные:
Сумма первоначальной инвестиции – 7000. В течение анализируемого периода было еще две инвестиции – 5040 и 10.
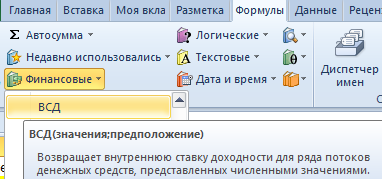
Заходим на вкладку «Формулы». В категории «Финансовые» находим функцию ВСД. Заполняем аргументы.
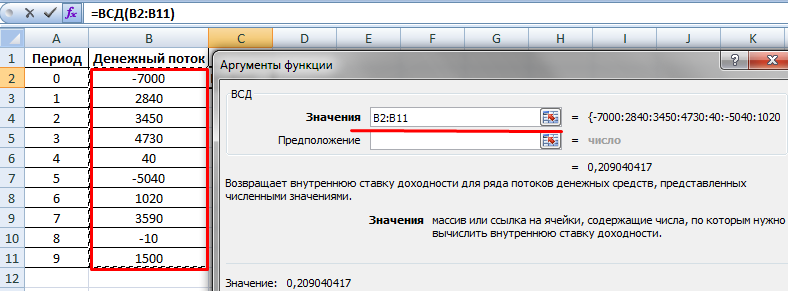
Значения – диапазон с суммами денежных потоков, по которым необходимо рассчитать внутреннюю норму рентабельности. Предположение – опустим.
Искомая IRR (внутренняя норма доходности) анализируемого проекта – значение 0,209040417. Если перевести десятичное выражение величины в проценты, то получим ставку 20,90%.
В нашем примере расчет ВСД произведен для ежегодных потоков. Если нужно найти IRR для ежемесячных потоков сразу за несколько лет, лучше ввести аргумент «Предположение». Программа может не справиться с расчетом за 20 попыток – появится ошибка #ЧИСЛО!.
Еще один показатель эффективности инвестиционного проекта – NPV (чистый дисконтированный доход). NPV и IRR связаны: IRR определяет ставку дисконтирования, при которой NPV = 0 (то есть затраты на проект равны доходам).
Для расчета NPV в Excel применяется функция ЧПС. Чтобы найти внутреннюю ставку доходности графическим методом, нужно построить график изменения NPV. Для этого в формулу расчета NPV будем подставлять разные значения ставок дисконта.
На основании полученных данных построим график изменения NPV.
Пересечение графика с осью Х (когда чистый дисконтированный доход проекта равняется нулю) дает показатель IRR для данного проекта. Графический метод показал результат ВСД, аналогичный найденному в Excel.
Как пользоваться показателем ВСД:
Если значение IRR проекта выше стоимости капитала для предприятия, то данный инвестиционный проект нужно принять.
То есть если ставка кредита меньше внутренней нормы рентабельности, то заемные средства принесут прибыль. Так как в при реализации проекта мы получим больший процент дохода, чем величина капитала.
Вернемся к нашему примеру. Допустим, для запуска проекта брался кредит в банке под 15% годовых. Расчет показал, что внутренняя норма доходности составила 20,9%. На таком проекте можно заработать.
Функция ВСД
В этой статье описаны синтаксис формулы и использование функции ВСД в Microsoft Excel.
Описание
Возвращает внутреннюю ставку доходности для ряда потоков денежных средств, представленных их численными значениями. В отличие от аннуитета, денежные суммы в пределах этих потоков могут колебаться. Однако обязательным условием является регулярность поступлений (например, ежемесячно или ежегодно). Внутренняя ставка доходности — это процентная ставка, принимаемая для инвестиции, состоящей из платежей (отрицательные величины) и доходов (положительные величины), которые имеют место в следующие друг за другом и одинаковые по продолжительности периоды.
Синтаксис
Аргументы функции ВСД описаны ниже.
Значения — обязательный аргумент. Массив или ссылка на ячейки, содержащие числа, для которых требуется подсчитать внутреннюю ставку доходности.
Значения должны содержать по крайней мере одно положительное и одно отрицательное значение.
В функции ВСД для интерпретации порядка денежных выплат или поступлений используется порядок значений. Убедитесь, что значения выплат и поступлений введены в нужном порядке.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, такие значения игнорируются.
Предположение — необязательный аргумент. Величина, предположительно близкая к результату ВСД.
Microsoft Excel вычисляет IRR методом итеративных методов. Начиная с предположения, IRR цикличен по вычислениям, пока не будет точным результат в пределах 0,00001 процента. Если IRR не может найти результат, который работает после 20 попыток, #NUM! возвращается значение ошибки.
В большинстве случаев для вычислений с помощью функции ВСД нет необходимости задавать аргумент «предположение». Если он опущен, предполагается значение 0,1 (10%).
Если функция ВСД возвращает значение ошибки #ЧИСЛО! или результат далек от ожидаемого, попробуйте повторить вычисление с другим значением аргумента «предположение».
Замечания
Функция ВСД тесно связана с функцией ЧПС. Ставка доходности, вычисляемая функцией ВСД, связана с нулевой чистой текущей стоимостью. Взаимосвязь функций ЧПС и ВСД отражена в следующей формуле:
ЧПС(ВСД(A2:A7),A2:A7) равняется 1.79E-09 [Учитывая точность расчета для функции ВСД, значение можно считать нулем).]
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Чистая приведенная стоимость NPV (ЧПС) и внутренняя ставка доходности IRR (ВСД) в EXCEL
history 3 февраля 2015 г.
Рассчитаем Чистую приведенную стоимость и Внутреннюю норму доходности с помощью формул MS EXCEL.
Начнем с определения, точнее с определений.
Чистой приведённой стоимостью (Net present value, NPV) называют сумму дисконтированных значений потока платежей, приведённых к сегодняшнему дню (взято из Википедии). Или так: Чистая приведенная стоимость – это Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций (сайт cfin. ru) Или так: Текущая стоимость ценной бумаги или инвестиционного проекта, определенная путем учета всех текущих и будущих поступлений и расходов при соответствующей ставке процента. (Экономика . Толковыйсловарь . — М . : « ИНФРА — М «, Издательство « ВесьМир «. Дж . Блэк .)
Для наших целей (расчет в MS EXCEL) определим NPV так: Чистая приведённая стоимость — это сумма Приведенных стоимостей денежных потоков, представленных в виде платежей произвольной величины, осуществляемых через равные промежутки времени.
CFn – это денежный поток (денежная сумма) в период n. Всего количество периодов – N. Чтобы показать, является ли денежный поток доходом или расходом (инвестицией), он записывается с определенным знаком (+ для доходов, минус – для расходов). Величина денежного потока в определенные периоды может быть =0, что эквивалентно отсутствию денежного потока в определенный период (см. примечание2 ниже). i – это ставка дисконтирования за период (если задана годовая процентная ставка (пусть 10%), а период равен месяцу, то i = 10%/12).
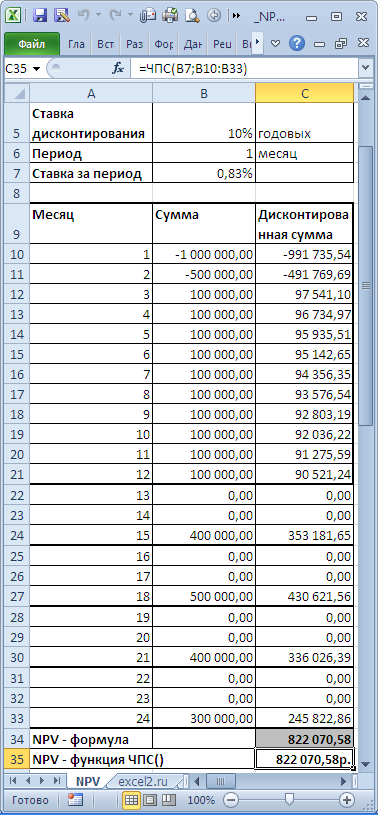
Определившись со сроками денежных потоков, для функции ЧПС() нужно найти наиболее короткий период между денежными потоками. Например, если в 1-й год поступления запланированы ежемесячно, а во 2-й поквартально, то период должен быть выбран равным 1 месяцу. Во втором году суммы денежных потоков в первый и второй месяц кварталов будут равны 0 (см. файл примера, лист NPV ).
О точности расчета ставки дисконтирования
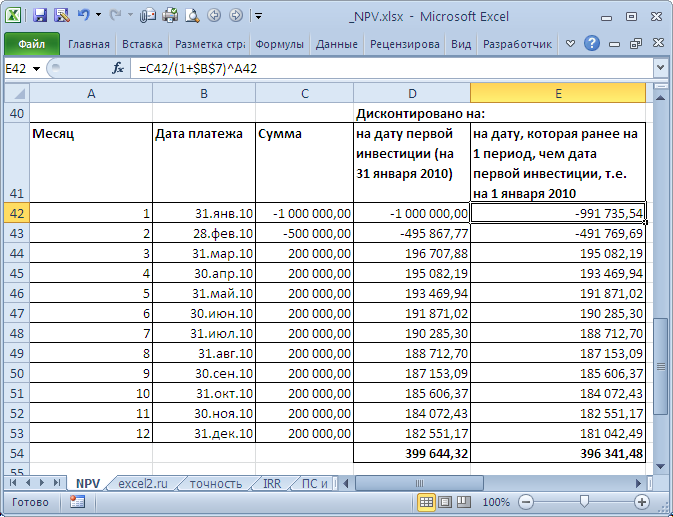
Существуют десятки подходов для определения ставки дисконтирования. Для расчетов используется множество показателей: средневзвешенная стоимость капитала компании; ставка рефинансирования; средняя банковская ставка по депозиту; годовой процент инфляции; ставка налога на прибыль; страновая безрисковая ставка; премия за риски проекта и многие другие, а также их комбинации. Не удивительно, что в некоторых случаях расчеты могут быть достаточно трудоемкими. Выбор нужного подхода зависит от конкретной задачи, не будем их рассматривать. Отметим только одно: точность расчета ставки дисконтирования должна соответствовать точности определения дат и сумм денежных потоков. Покажем существующую зависимость (см. файл примера, лист Точность ).
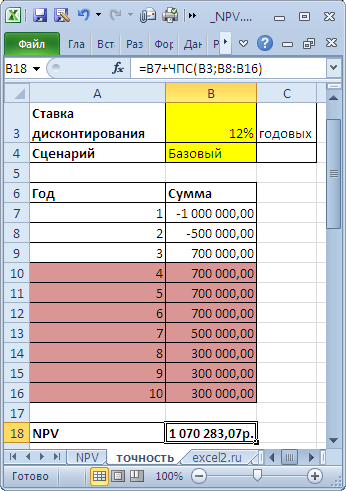
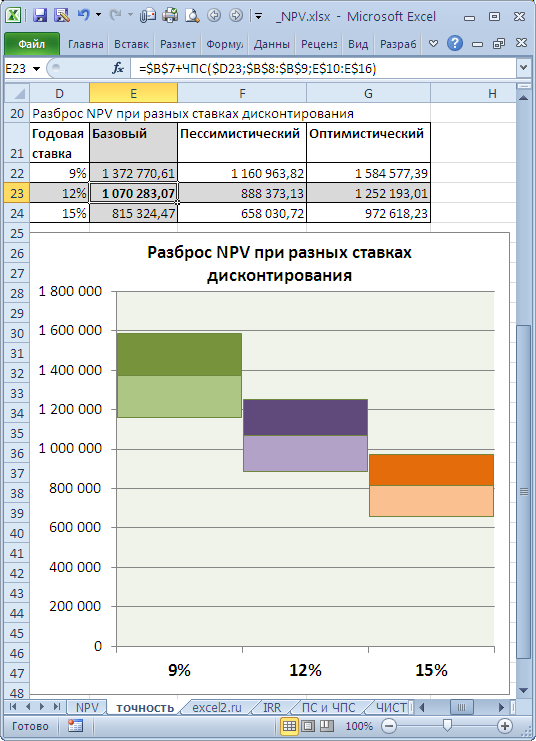
Пусть имеется проект: срок реализации 10 лет, ставка дисконтирования 12%, период денежных потоков – 1 год.
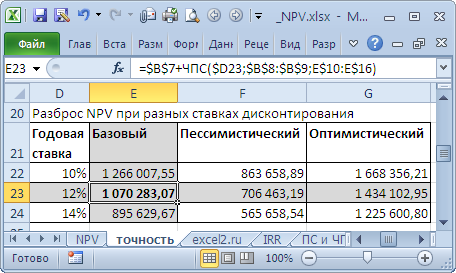
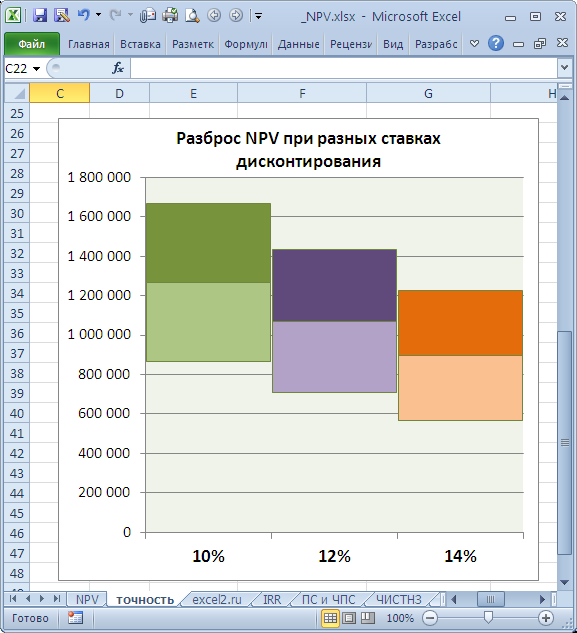
NPV составил 1 070 283,07 (Дисконтировано на дату первого платежа). Т.к. срок проекта большой, то все понимают, что суммы в 4-10 году определены не точно, а с какой-то приемлемой точностью, скажем +/- 100 000,0. Таким образом, имеем 3 сценария: Базовый (указывается среднее (наиболее «вероятное») значение), Пессимистический (минус 100 000,0 от базового) и оптимистический (плюс 100 000,0 к базовому). Надо понимать, что если базовая сумма 700 000,0, то суммы 800 000,0 и 600 000,0 не менее точны. Посмотрим, как отреагирует NPV при изменении ставки дисконтирования на +/- 2% (от 10% до 14%):
Рассмотрим увеличение ставки на 2%. Понятно, что при увеличении ставки дисконтирования NPV снижается. Если сравнить диапазоны разброса NPV при 12% и 14%, то видно, что они пересекаются на 71%.
Много это или мало? Денежный поток в 4-6 годах предсказан с точностью 14% (100 000/700 000), что достаточно точно. Изменение ставки дисконтирования на 2% привело к уменьшению NPV на 16% (при сравнении с базовым вариантом). С учетом того, что диапазоны разброса NPV значительно пересекаются из-за точности определения сумм денежных доходов, увеличение на 2% ставки не оказало существенного влияния на NPV проекта (с учетом точности определения сумм денежных потоков). Конечно, это не может быть рекомендацией для всех проектов. Эти расчеты приведены для примера. Таким образом, с помощью вышеуказанного подхода руководитель проекта должен оценить затраты на дополнительные расчеты более точной ставки дисконтирования, и решить насколько они улучшат оценку NPV.
Совершенно другую ситуацию мы имеем для этого же проекта, если Ставка дисконтирования известна нам с меньшей точностью, скажем +/-3%, а будущие потоки известны с большей точностью +/- 50 000,0
Увеличение ставки дисконтирования на 3% привело к уменьшению NPV на 24% (при сравнении с базовым вариантом). Если сравнить диапазоны разброса NPV при 12% и 15%, то видно, что они пересекаются только на 23%.
Таким образом, руководитель проекта, проанализировав чувствительность NPV к величине ставки дисконтирования, должен понять, существенно ли уточнится расчет NPV после расчета ставки дисконтирования с использованием более точного метода.
После определения сумм и сроков денежных потоков, руководитель проекта может оценить, какую максимальную ставку дисконтирования сможет выдержать проект (критерий NPV = 0). В следующем разделе рассказывается про Внутреннюю норму доходности – IRR.
Внутренняя ставка доходности IRR (ВСД)
Достоинством IRR состоит в том, что кроме определения уровня рентабельности инвестиции, есть возможность сравнить проекты разного масштаба и различной длительности.
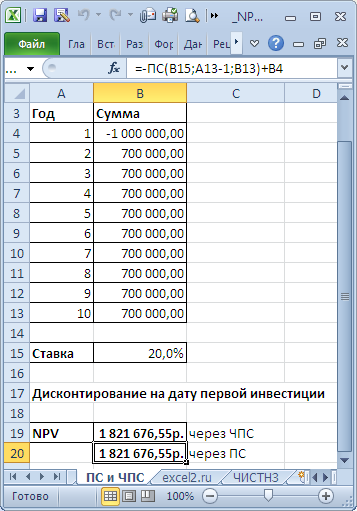
Расчет NPV при постоянных денежных потоках с помощью функции ПС()
Напомним, что аннуитет представляет собой однонаправленный денежный поток, элементы которого одинаковы по величине и производятся через равные периоды времени. В случае, если предполагается, что денежные потоки по проекту одинаковы и осуществляются через равные периоды времени, то для расчета NPV можно использовать функцию ПС() (см. файл примера, лист ПС и ЧПС ).
Расчет приведенной стоимости платежей, осуществляемых за любые промежутки времени
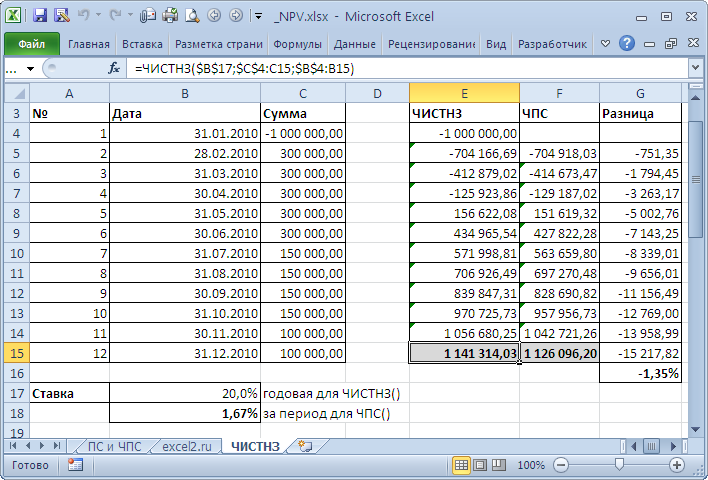
Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция ЧИСТНЗ() (английский вариант – XNPV()).
Функция ЧИСТНЗ() возвращает Чистую приведенную стоимость для денежных потоков, которые не обязательно являются периодическими. Расчеты выполняются по формуле:
Где, dn = дата n-й выплаты; d1 = дата 1-й выплаты (начальная дата); i – годовая ставка.
Это связано с тем, что у ЧИСТНЗ() длительность периода (месяц) «плавает» от месяца к месяцу. Даже если вместо месяца взять 30 дней, то в этом случае разница получается из-за того, что 12*30 не равно 365 дням в году (ставка у ЧПС() указывается за период, т.е. Годовая ставка/12). В случае, если денежные потоки осуществляются ежегодно на одну и туже дату, расчеты совпадают (если нет високосного года).
Внутренняя ставка доходности ЧИСТВНДОХ()
Расчеты в функции ЧИСТВНДОХ() производятся по формуле:
Где, Pi = i-я сумма денежного потока; di = дата i-й суммы; d1 = дата 1-й суммы (начальная дата, на которую дисконтируются все суммы).