Все что находится в природе математически точно и определенно
Интродукция
Михаил Васильевич Ломоносов
Интродукция
Интродукция
Интродукция
Интродукция
Интродукция
Интродукция
«Предмет математики настолько серьезен, что полезно не упускать случая сделать его немного занимательным»,- повторял Блез Паскаль, один из великих ученых прошлого.
Интродукция
Интродукция
«Наука и искусство так же тесно связаны между собой, как легкие и сердце»,- писал Лев Николаевич Толстой. Ему, великому писателю, вторят прославленные на весь мир ученые.
А. Е. Арбузов, химик-органик: «Не могу представить себе химика, не знакомого с высотами поэзии, с картинами мастеров живописи, с хорошей музыкой. Вряд ли он создаст что-либо значительное в своей области».
А. А. Потебня, филолог-славист: «Поэзия. не изредка, от времени к времени, а постоянно служит источником науки, которая в свою очередь питает новое поэтическое творчество».
B. И. Вернадский, геохимик, биогеохимик, радиогеолог: «Ученые, натуралисты в том числе, часто бывали и художниками в широком смысле этого слова».
И. И. Мечников, биолог: «Великими мастерами в искусстве становятся люди ученые, владеющие математикой и измерительными методами, как, например, Альберти, Леонардо да Винчи, Микеланджело».
C. В. Ковалевская, математик: «Мне кажется, что поэт должен только видеть то, чего не видят другие, видеть глубже других. И это же должен и математик».
Эти высказывания, касающиеся науки вообще, а математики лишь в частности, особо применимы к геометрии. Ее внутренняя гармония, строгая и законченная красота не только делают геометрию наукой о фундаментальных свойствах объективного, существующего независимо от нас, нашего сознания мира, но и дают каждому из нас возможность пройти несколько шагов по геометрической стезе. «Если бы только удалось преодолеть то недоверие, с которым весьма многие под влиянием случайных школьных впечатлений сторонятся всего, что связано с математикой, то людей, склонных «импровизировать» в области несложных произведений математического искусства, оказалось бы не меньше, чем активных любителей музыки»,- пишут Ганс Радемахер и Отто Теплиц в своей книге «Числа и фигуры».
Интродукция
Попытка преодолеть это недоверие и есть основной мотив предлагаемой вашему вниманию геометрической рапсодии.
Все что находится в природе математически точно и определенно
Высказывания М. В. Ломоносова о науке и языке:
Ø Не для того мы живем на свете, чтобы насыщаться, но для того насыщаемся, чтобы жить.
Ø Наука есть вождь к познанию правды, просвещение разума, успокоение народов.
Ø Легко быть философом, выучась произносить три слова: «Бог так сотворил», и сие дав в ответ вместо всех причин.
Ø Ни единому человеку не запрещено в университетах учиться, кто бы он ни был, и в университете студент тот почтеннее, кто больше научился, а чей он сын в том нет нужды.
Ø Природа крепко держится своих законов и всюду одинакова.
Ø Химик без знания физики подобен человеку, который всего должен искать ощупом. И сии две науки так соединены между собой, что одна без другой в совершенстве быть не могут.
Ø Я бы охотно молчал и жил в покое, да боюсь наказания от правосудия и всемогущего промысла, который не лишил меня дарования и прилежания в учении и ныне дозволил случай, дал терпение и благородную упрямку и смелость к преодолению всех препятствий к распространению наук в отечестве, что всего в жизни моей дороже.
Ø Честь российского народа требует, чтоб показать способность и остроту его в науках.
Ø Выспрашивать у осторожной и догадливой геометрии, советоваться с точною и замысловатою механикою, выведывать через проницательную оптику.
Ø Велико есть дело, смертными и преходящими трудами дать бессмертие множеству народа, соблюсти похвальных дел добрую славу и, перенося минувшие деяния в потомство и в глубокую вечность, соединить тех, которых натура долготою времени разделила. Мрамор и металл, коими вид и дела великих людей, изображенные всенародно возвышаются, стоят на одном месте неподвижно и ветхостью разрушаются. История, повсюду распростираясь и обращаясь в руках человеческого рода, стихии строгость и грызение древности презирает.
Ø Один опыт я ставлю выше, чем тысячу мнений, рожденных только воображением.
Ø Науки сами все дела человеческие приводят наверх совершенства, что их благороднее, что полезнее, что увеселительнее и что бесспорнее в делах человеческих быть может.
Ø Все, что находится в природе, математически точно и определенно; и если иногда мы сомневаемся в этой точности, то наше невежество ничего не отнимает от этой достоверности; если бы весь мир сомневался в том, что дважды два – четыре, то все-таки у всех сомневающихся дважды два дадут четыре.
Ø Велико есть дело достигнуть во глубину земную разумом, куда руками и оку досягнуть возбраняет натура; странствовать размышлением в преисподней, проникнуть рассуждением сквозь тесные расселины и вечной ночью, помраченные вещи и деяния выводить на солнечную ясность.
Ø Украшение есть изобретенных идей пристойными и избранными речениями изображение. Состоит в чистоте штиля, в течение слова, в великолепии и силе оного.
1.3. Подборка «ломоносовских» афоризмов
I. Слово о М.В. Ломоносове
1. Любой век, любая эпоха нашей народной жизни всегда приукрашена чьей-либо особо яркой и могучей жизнью, деяниями особо славными. Многие звезды украшали русское небо восемнадцатого столетия. Звездою первой величины явилась слава Михаила Ломоносова (Б. Шергин).
2. Он создал первый университет, он, лучше сказать, сам был нашим первым университетом (А.С. Пушкин).
3. Соединяя необыкновенную силу воли с необыкновенною силою понятия, Ломоносов обнял все отрасли просвещения. Жажда науки была сильнейшею страстью сей души, исполненной страстей. Историк, ритор, механик, химик, минералог, художник и стихотворец, он все испытал и все проник: первый углубляется в историю Отечества, утверждает правила общественного языка его, дает законы и образцы классического красноречия, с несчастным Рихманом предугадывает открытия Франклина, учреждает фабрику, сам сооружает махины, дарит художества мозаическими произведениями и, наконец, открывает нам истинные истоки нашего поэтического языка (А.С. Пушкин).
4. Догадки Ломоносова тем большую имеют цену, что они удачно задуманы и вероподобны (Л. Эйлер).
5. На берегах Ледовитого моря, подобно северному сиянию, блеснул Ломоносов. Ослепительно и прекрасно было это явление. Оно доказало собой, что человек есть человек во всяком состоянии и во всяком климате, что гений умеет торжествовать над всеми препятствиями, какие не противопоставляет ему враждебна судьба, что, наконец, русский способен ко всему великому и прекрасному (В.Г. Белинский).
6. С Ломоносова начинается наша литература; он был ее отцом и пестуном (В.Г. Белинский).
7. Ломоносов страстно любил науку, но думал и заботился исключительно о том, что нужно было для блага его Родины (К.Г. Чернышевский).
8. Как по своему энциклопедизму, да и по своей легкости восприятия этот знаменитый ученый был типом русского человека… Он был горняком, химиком, поэтом, филологом, физиком, астрономом и историком… Его ясный ум, полный беспокойного желания понять, оставляя один предмет, чтобы овладеть другим, с удивительной легкостью постигая его (А.И. Герцен).
Славься, славься, великий муж!
Ты насадитель наук на Руси!
Доброе семя посеял ты в ней!
Жатва все зреет – что год, то пышней!
Лет немного пройдет,
И вся Русь их пожнет;
Весь народ возгласит:
Память вовек Ломоносову!
(Кантата в честь Ломоносова, музыка М.И. Глинки)
11. Деятельность Ломоносова всегда целеустремленно связана с наиболее важными потребностями страны, с ее промышленным, культурным развитием… Историческое значение Ломоносова состоит также и в том, что он настойчиво добивался широкого развития образования в России, привлечения в науку способных людей из народа, показав на личном примере, на какие подвиги способны люди для своей Родины. Ломоносов принадлежит не только истории (М.В. Келдыш).
12. Только теперь, спустя два века, можно с достаточной полнотой охватить и должным образом оценить все сделанное этим удивительным богатырем науки. Достигнутое им в области физики, химии, астрономии, приборостроения, геологии, географии, языкознания, истории достойно было бы деятельности целой Академии (С.И. Вавилов).
13. Не камень со иссечением имени твоего принесет славу твою в будущие столетия. Слово твое, живущее присно и во веки в творениях твоих, слово российского племени, тобою в языке нашем обновленное, прилетит в устах народных за необозримый горизонт столетий (А.Н. Радищев).
14. Все должен был сделать сам, всему положить начало (В.Г. Белинский).
II. Афоризмы М.В. Ломоносова о науке и языке
1. Не для того мы живем на свете, чтобы насыщаться, но для того насыщаемся, чтобы жить.
2. Наука есть вождь к познанию правды, просвещение разума, успокоение народов.
3. Легко быть философом, выучась произносить три слова: «бог так сотворил», и сие дав в ответ вместо всех причин.
4. Ни единому человеку не запрещено в университетах учиться, кто бы он ни был, и в университете студент тот почтеннее, кто больше научился, а чей он сын в том нет нужды.
5. Природа крепко держится своих законов и всюду одинакова.
6. Химик без знания физики подобен человеку, который всего дол-жен искать ощупом. И сии две науки так соединены между собой, что одна без другой в совершенстве быть не могут.
7. Оных людей, которые бедственными трудами или паче исполинскою смелостью тайны естественные испытать тщатся, не надлежит почитать продерзкими, но мужественными и великодушными.
8. Я бы охотно молчал и жил в покое, да боюсь наказания от правосудия и всемогущего промысла, который не лишил меня дарования и прилежания в учении и ныне дозволил случай, дал терпение и благородную упрямку и смелость к преодолению всех препятствий к распространению наук в отечестве, что всего в жизни моей дороже.
9. Честь российского народа требует, чтоб показать способность и остроту его в науках.
10. Выспрашивать у осторожной и догадливой геометрии, …советоваться с точною и замысловатою механикою, выведывать через проницательную оптику.
11. Велико есть дело, смертными и преходящими трудами дать бессмертие множеству народа, соблюсти похвальных дел добрую славу и, перенося минувшие деяния в потомство и в глубокую вечность, соединить тех, которых натура долготою времени разделила. Мрамор и металл, коими вид и дела великих людей, изображенные всенародно возвышаются, стоят на одном месте неподвижно и ветхостью разрушаются. История, повсюду распростираясь и обращаясь в руках человеческого рода, стихии строгость и грызение древности презирает.
12. Один опыт я ставлю выше, чем тысячу мнений, рожденных только воображением.
13. Науки сами все дела человеческие приводят наверх совершенства, что их благороднее, что полезнее, что увеселительнее и что бесспорнее в делах человеческих быть может.
14. Все, что находится в природе, математически точно и определенно; и если иногда мы сомневаемся в этой точности, то наше невежество ничего не отнимает от этой достоверности; если бы весь мир сомневался в том, что дважды два – четыре, то все-таки у всех сомневающихся дважды два дадут четыре.
16. Велико есть дело достигнуть во глубину земную разумом, куда руками и оку досягнуть возбраняет натура; странствовать размышлением в преисподней, проникнуть рассуждением сквозь тесные расселины и вечной ночью, помраченные вещи и деяния выводить на солнечную ясность.
17. Украшение есть изобретенных идей пристойными и избранными речениями изображение. Состоит в чистоте штиля, в течении слова, в великолепии и силе оного.
Данный текст является ознакомительным фрагментом.
ЛОМОНОСОВ. Академик. Вольнодумец. Христианин.
Цитаты Ломоносова
Подготовил: Дмитрий Сироткин
Представляю вам подборку цитат ученого и поэта Михаила Ломоносова (1711—1765).
Удивительная для своего времени история научной и придворной карьеры этого выходца из народа широко известна.
Цитаты сгруппированы по темам: наука, жизненная этика, Россия, русский язык, отдельные науки, религия и наука, о себе, люди, природа, брак, астрономия, невежды, журналисты, любовь, жизнь.
О науке
Науки юношей питают, Отраду старцам подают, В счастливой жизни украшают, В несчастный случай берегут…
Везде исследуйте всечасно, Что есть велико и прекрасно.
Наука есть ясное познание истины, просвещение разума, непорочное увеселение жизни, похвала юности, старости подпора, строительница градов, полков, крепость успеха в несчастии, в счастии — украшение, везде верный и безотлучный спутник.
Испытание натуры трудно, однако приятно, полезно, свято. Чем больше таинства ее разум постигает, чем долее рачение наше в оной простирается, тем обильнее собирает плоды для потребностей житейских.
Разум с помощью науки проникает в тайны вещества, указывает, где истина. Наука и опыт — только средства, только способы собирания материалов для разума.
Один опыт я ставлю выше, чем тысячу мнений, рожденных только воображением.
О, если бы все труды, заботы, издержки и бесконечное множество людей, истребляемые и уничтожаемые свирепством войны, были обращены на пользу мирного научного мореплавания!
Кстати, цитаты про науку
О жизненной этике
Дерзайте отчизну мужеством прославить.
Неусыпный труд все препятствия преодолевает.
Кто малого не может, тому и большее невозможно.
Ежели ты что хорошее сделаешь с трудом, труд минется, а хорошее останется, а ежели сделаешь что худое с услаждением, услаждение минется, а худое останется.
Иногда промедление смерти подобно.
Ошибки замечать не много стоит: дать нечто лучшее — вот что приличествует достойному человеку.
Ничто не происходит без достаточного основания.
Кто достигнет старости, тот почувствует болезни от роскошей, бывших в юности, следовательно, в молодых летах должно от роскошей удаляться.
О России
Народ российский от времен, глубокою древностию сокровенных, до нынешнего веку толь многие видел в счастии своем перемены, что ежели кто междоусобные и отвне нанесенные войны рассудит, в великое удивление придет, что по толь многих разделениях, утеснениях и нестроениях не токмо не расточился, но и на высочайший степень величества, могущества и славы достигнул.
Что может собственных Платонов И быстрых разумом Невтонов Российская земля рождать.
Только в бодром горячем порыве, в страстной любви к своей родной стране, смелости и энергии родится победа. И не только и не столько в отдельном порыве, сколько в упорной мобилизации всех сил, в том постоянном горении, которое медленно и неуклонно сдвигает горы, открывает неведомые глубины и выводит их на солнечную ясность.
Могущество и обширность морей, Российскую империю окружающих, требуют рачения и знания. Между прочим Северный океан есть пространное поле, где усугубиться может российская слава, соединенная с беспримерною пользою, чрез изобретение восточно-северного мореплавания в Индию и Америку.
Рачения и трудов для сыскания металлов требует пространная и изобильная Россия. Мне кажется, я слышу, что она к сынам своим вещает: «Простирайте надежду и руки ваши в мое недро и не мыслите, что искание ваше будет тщетно».
О русском языке
Повелитель многих языков, язык российский не только обширностью мест, где он господствует, но купно собственным своим пространством и довольствием велик перед всеми в Европе.
Язык, которым Российская держава великой части света повелевает, по ея могуществу имеет природное изобилие, красоту и силу, чем ни единому европейскому языку не уступает. И для того нет сумнения, чтобы российское слово не могло приведено быть в такое совершенство, каковому в других удивляемся.
Красота, величие, сила и богатство российского языка явствуют довольно из книг, в прошлые века писанных, когда еще не токмо никаких правил для сочинений наши предки не знали, но и о том едва ли думали, что оные есть или могут быть.
Карл Пятый, римский император, говаривал, что гишпанским языком с Богом, французским — с друзьями, немецким — с неприятелем, ита-лианским — с женским полом говорить прилично. Но если бы он российскому языку был искусен, то, конечно, к тому присовокупил бы, что им со всеми оными говорить пристойно, ибо нашел бы в нем великолепие гишпанского, живость французского, крепость немецкого, нежность италианского, сверх того богатство и сильную в изображениях кратость греческого и латинского языков.
Об отдельных науках
Математику уже за то любить следует, что она ум в порядок приводит.
Истинный химик должен быть не только практиком и теоретиком – он должен быть еще и философом.
Сколько происходит пользы от географии человеческому роду, о том всяк, имеющий понятие о всенародных прибытках, удобно рассудить может. Едино представление положения государств, а особливо своего отечества производит в сердце великое удовольствие…
Полезнейшая роду человеческому есть медицина.
Без грамматики оратория – глупа, поэзия – косноязычна, философия – безосновательна, история – непонятна, юриспруденция – сомнительна.
О религии и науке
Не здраво рассудителен математик, ежели он хочет божескую волю вымерять циркулем. Таков же и богословия учитель, если он думает, что по псалтире научиться можно астрономии или химии.
Духовенству к учениям, правду физическую для пользы и просвещения показующим, не привязываться, а особливо не ругать наук в проповедях.
У многих глубоко укоренилось убеждение, что метод философствования, опирающийся на атомы, либо не может объяснить происхождения вещей, либо, поскольку может, отвергает Бога, как Творца. И в том, и в другом они, конечно, глубоко ошибаются, ибо нет никаких природных начал, которые могли бы яснее и полнее объяснить сущность материи и всеобщего движения, и никаких, которые с большей настоятельностью требовали бы существования всемогущего двигателя.
Правда и вера суть две сестры родные, дочери одного всевышнего родителя, никогда в распрю между собой прийти не могут, разве кто из некоторого тщеславия и показания собственного мудрствования восклеплет.
О себе
Не токмо у стола знатных господ или у каких земных владетелей дураком быть не хочу, ниже у самого Господа Бога, который дал мне смысл, пока разве отнимет.
За то терплю, что стараюсь защитить труды Петра Великого, чтобы выучились россияне, чтобы показали своё достоинство pro aris etc.
За общую пользу, а особливо за утверждение наук в отечестве, и против отца своего родного восстать за грех не ставлю… Я к сему себя посвятил, чтобы до гроба моего с неприятелями наук российских бороться, как уже борюсь двадцать лет, стоял за них смолоду, на старости не покину.
Люблю правду всем сердцем, как всегда любил и любить буду до смерти.
Одно спасенье мне – не ожидать спасенья.
О людях
Кто в свете сем родился волком, тому лисицой не бывать.
Малый человек и на горе мал, а исполин велик и в яме.
Ленивый человек в бесчестном покое сходен с неподвижною болотною водою, которая, кроме смраду и презренных гадин, ничего не производит.
О природе
Природа весьма проста; что этому противоречит, должно быть отвергнуто.
Природа держится своих законов самым крепким образом даже в малейшем, чем мы пренебрегаем.
Все, что есть в природе, математически точно и определенно; хотя мы иногда сомневаемся в этой точности, но наше незнание нисколько не умаляет ее: если бы даже весь мир сомневался в том, что дважды два четыре, все-таки дважды два у всех сомневающихся дадут четыре.
О браке
Жениться хорошо, да много и досады. Я слова не скажу про женские наряды: Кто мил, на том всегда приятен и убор; Хоть правда, что при том и кошелек неспор.
Но он ответствовал: «Я, братец, признаваюсь, Что век она жила со мною вопреки; То истинно теперь о том не сомневаюсь, Что, потонув, она плыла против реки».
Есть дети, следовательно, должны быть у них отцы и матери.
Об астрономии
Открылась бездна звезд полна; Звездам числа нет, бездне дна.
Идолопоклонническое суеверие держало астрономическую землю в своих челюстях, не давая ей двигаться.
Что в том Коперник прав, Я правду докажу, на Солнце не бывав. Кто видел простака из поваров такова, Который бы вертел очаг кругом жаркова?
О невеждах
Те, кто пишут темно, либо невольно выдают свое невежество, либо намеренно скрывают его. Смутно пишут о том, что смутно себе представляют.
Легко быть философом, выучась наизусть три слова: бог так сотворил; и сие дая в ответ вместо всех причин.
Нет такого невежды, который не мог бы задать больше вопросов, чем может их разрешить самый знающий человек.
О журналистах
Журналист не должен торопиться порицать гипотезы. Оные единственный путь, которым величайшие люди успели открыть истины самые важные.
Журналист никогда не должен создавать себе слишком высокого представления о своем превосходстве, о своей авторитетности, о ценности своих суждений. Ввиду того, что деятельность, которой он занимается, уже сама по себе неприятна для самолюбия тех, на кого она распространяется, он оказался бы совершенно неправ, если бы сознательно причинял им неудовольствие и вынуждал их выставлять на свет его несостоятельность.
О любви
Любовь сильна, как молния, но без грому проницает, и самые сильные ее удары приятны.
Любовь есть склонность духа к другому кому, чтобы из его благополучия иметь услаждение.
О жизни
Худые примеры не закон.
То, что нашим предкам казалось странным, неясным и пугающим, для нас вполне доступно, понятно и приятно.
О разном
Что касается тех мистических писателей, которые уклоняются от сообщения своих знаний, то они с меньшим уроном для своего доброго имени и с меньшей тягостью для своих читателей могли бы скрыть это учение, если бы вовсе не писали книг, вместо того, чтобы писать плохие.
Тому, кто хочет говорить красиво, необходимо уметь говорить правильно и иметь достаточный запас слов, которыми можно высказать мысли.
Все великие люди честь и похвальбу любили… Без сей страсти не чинились бы на свете знатные предприятия и великие дела к концу бы не приходили.
В приведенных цитатах Михаила Ломоносова чувствуется энергия и воля целеустремленного человека. Как известно, отнюдь не все его планы и идеи удалось осуществить, но и то, что получилось дало мощный толчок развитию российской науки.
Цитаты про Ломоносова
Далее вы можете прочитать подборку фразеологизмов Ломоносова и другие подборки цитат:
Буду признателен, если вы поделитесь с друзьями ссылкой на статью в социальных сетях. Воспользуйтесь кнопками сетей ниже.
Комментарии также всячески приветствуются!
Структура книги
Труд М. В. Ломоносова написан более чем на 300 страницах. Пересказать его достаточно сложно. Отметим основные части книги:
В своей книге по ораторскому искусству ученый пишет о том, что все публичные выступления должны строиться на логике, излагаться грамотно, литературным языком. Каждому выступающему необходимо тщательно составлять речь, подкреплять свои слова примерами.
Ученый считал, что любой человек в состоянии заниматься развитием красноречия. Каждый может научиться искусству оратора.
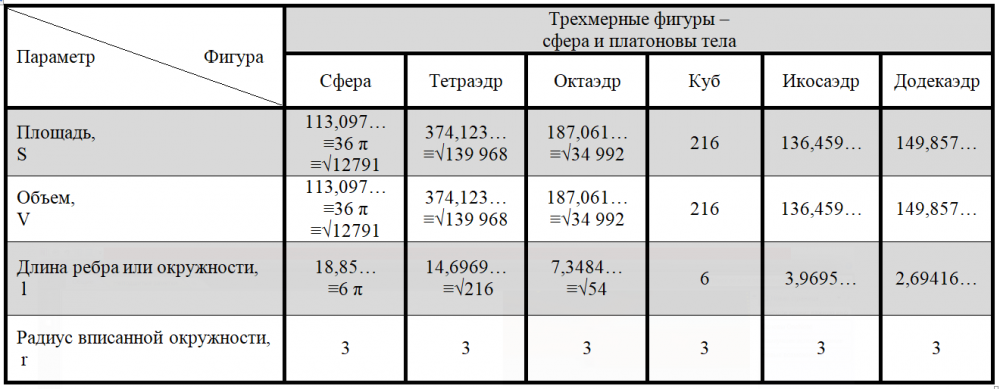
Платоновы тела как структурированные геометрические объекты
«Книга природы написана на языке математики»
«Числа не управляют миром, но они показывают, как управляется мир»
«Все, что находится в природе, математически точно и определенно»
Аннотация. Показана возможность построения платоновых тел из структурных элементов – треугольников Кеплера (соотношение катетов 1:√1,618..) и Фибоначчи (соотношение катетов 1:1,618…) – при условии неизменности площади названных элементов. Количество элементов (или пар элементов) составляющих структуру «тетраэдра», «октаэдра», «куба» увеличивается, таким образом, в два раза, а «икосаэдра» – в пять раз по отношению к количеству элементов тетраэдра при неизменности показателя «площадь всех структурных элементов фигуры» и радиуса (r=3) вписанной в платоновы тела сферы. Кроме того, площадь структурных элементов двух додекаэдров (Sc.э.2дод.=√959 325) равна площади структурных элементов любых 5-ти платоновых тел, например, 5-ти тетраэдров (или октаэдров, кубов, икосаэдров) (Sc.э.1пл.т.=√38 373). Показанная возможность находится в соответствии с текстом произведения Платона «Тимей», согласно которому – платоновы тела могут «перерождаться друг в друга… ».
Ключевые слова: платоновы тела, структурированные геометрические объекты, структурные элементы, золотая пропорция, треугольник Кеплера, треугольник Фибоначчи, математическое тождество.
Введение
По результатам анализа геометрии одного из помещений пирамиды Хуфу «Камера Царя» выявлено, что линейные размеры пола помещения вмещают два прямоугольных треугольника со следующими свойствами: значение площади прямоугольного треугольника математически тождественно значению его периметра (P=27,4164078649986…), а так же – квадрата меньшего катета (27,4164078649986…≡Lм.кат.5,236067977499784… 2 ) [3, 4] (математическое тождество – равенство, выполняющееся на всём множестве значений входящих в него переменных). В этой связи нами были определены возможные значения при тождестве площади и периметра у двумерных фигур, объема и площади – у трехмерных. На основании проведенного исследования, обобщая наблюдаемые значения тождеств в связи со значениями радиуса вписанной окружности, сформулирована теорема:
«в правильных двумерных и выпуклых трехмерных геометрических фигурах радиус вписанной окружности (радиус сферы для трехмерных фигур) при тождестве площади и периметра (площади и объема для трехмерныхфигур) одинаков (равен 2 для двумерных и 3 для трехмерных)»[4].
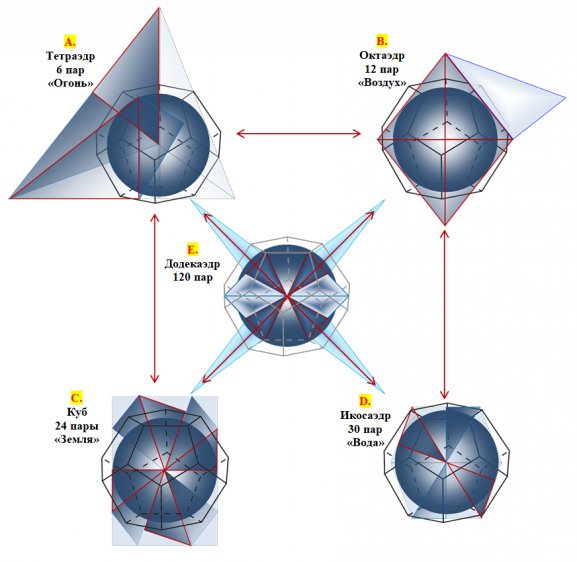
Кроме того, в одной из публикаций [2], нами показана возможность построения геометрии платоновых тел посредством двух треугольников, катеты которых обладают соотношением меры золотой пропорции – треугольника Кеплера (1:√Ф) и треугольника Фибоначчи (1:Ф). В статье показано, что «среди четырех платоновых тел (неправильные тетраэдр и правильные – октаэдр, куб, икосаэдр) имеется определенная числовая закономерность: количество пар треугольников Кеплера и Фибоначчи в определенной нами геометрической структуре этих тел по порядку их усложнения (от тетраэдра, октаэдра и до куба) увеличивается ровно в два раза (6 пар – в тетраэдре, 12 пар – в октаэдре, 24 пары – в кубе), а увеличение количества пар элементов (треугольников Кеплера и Фибоначчи) между кубом и икосаэдром – ровно в 2,5 раза (24 пары и 60 пар)» [2]. Результаты этого построения мы связали с информацией текста произведения «Тимей» [5]. Платон в своем произведении описывает ряд «перерождений» тел:
В этой связи нами сделано предположение:
для перехода (перерождения) платоновых тел друг в друга необходима некоторая постоянная величина (параметр) при прочих переменных. В качестве подобной величины (параметра) предполагается использовать параметр «площадь структурных элементов» (треугольников Кеплера и Фибоначчи), а в качестве переменной – их кратное количество в «структуре» платоновых тел.
Основная часть
Для проверки предположения сформулированы следующие задачи:
Для решения поставленных первых двух задач мы использовали геометрическое двухмерное плоскостное построение или, иначе говоря, геометрическое построение плоских фигур. Построенные структурированные геометрические объекты – платоновы тела «тетраэдр» и «октаэдр» – отличаются от их традиционного вида (представления) в том отношении, что они не являются правильными многогранниками (более подробно об этом в статье [2]).
Для построения платоновых тел «тетраэдр», «октаэдр», «куб», «икосаэдр» из структурных элементов – треугольников Кеплера и Фибоначчи – должны выполняться следующие условия (обозначенные нами ранее в статье [2]):
Кроме вышеназванных условий построения платоновых тел нами было обозначено еще одно исходное условие: для построения платоновых тел из структурных элементов – треугольников Кеплера и Фибоначчи – должны быть использованы параметры математической тождественности значений объема и площади этих геометрических фигур как исходные (таблица 1) [4]. При этом, в качестве единиц измерения длин и площадей структурных элементов, должны быть использованы условные единицы измерения (далее по тексту – у. е.). В качестве единицы измерения меры длины нами принята мера равная 1/3 части (=1 у.е.) радиуса вписанной в платоновы тела сферы (величина параметра «радиус вписанной сферы» неизменен).
Таблица 1 – Математическое тождество значений объема и площади сферы и платоновых тел [4] Учитывая вышеназванные условия, мы исследовали возможность построения платоновых тел из структурных элементов – треугольников Кеплера и Фибоначчи – при условии неизменности площади названных элементов в каждом из платоновых тел – и получили следующие варианты структурированных геометрических объектов (рисунки 1, 2, 3, 4, 5, 6, 7, 8, 9, 10). При этом (как было отмечено ранее [2]), среди четырех платоновых тел (неправильные тетраэдр и октаэдр, а так же – правильные куб, икосаэдр) имеется определенная числовая закономерность: отношение пар треугольников Кеплера и Фибоначчи в определенной нами геометрической структуре этих тел (от тетраэдра, октаэдра и до куба) увеличивается ровно в 2 раза (6 пар структурных элементов – в тетраэдре, 12 пар структурных элементов – в октаэдре, 24 пары структурных элементов – в кубе). А увеличение количества пар структурных элементов между тетраэдром и икосаэдром (30 пар структурных элементов) – ровно в 5 раз, а между икосаэдром и додекаэдром (120 пар структурных элементов) – ровно в 4 раза. Для удобства описания структурированных геометрических объектов нами определены треугольники Кеплера как «структурные элементы 1-го семейства», а треугольники Фибоначчи, соответственно, – как «структурные элементы 2-го семейства».
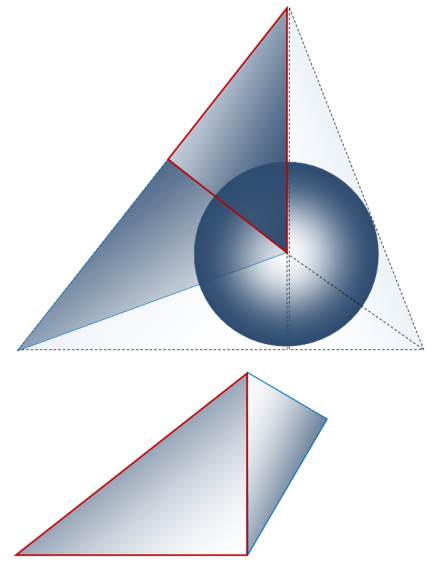
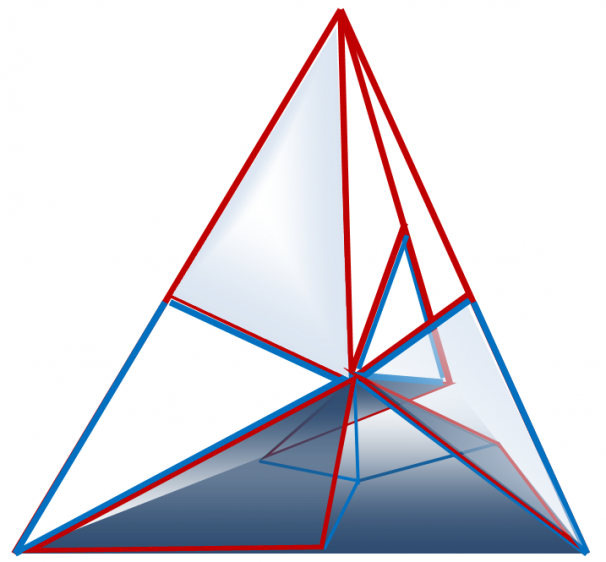
Построение неправильного тетраэдра (12 структурных элементов в 6 парах)
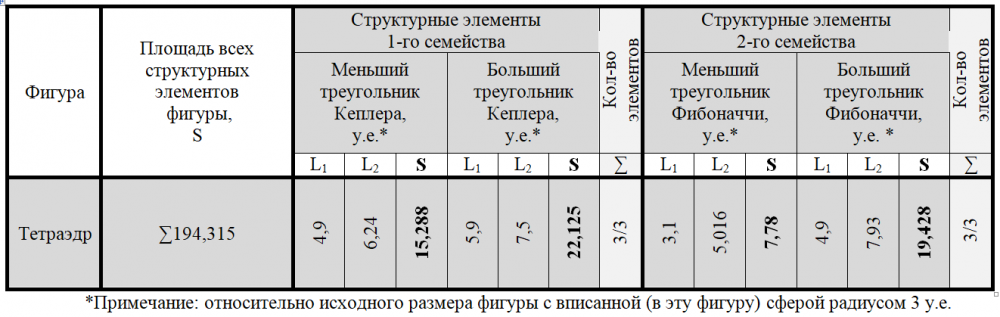
Для построения неправильного тетраэдра нами использовано шесть пар треугольников Кеплера и Фибоначчи различных размеров (по три больших и три малых треугольников Кеплера и Фибоначчи) (таблица 2).
Таблица 2 – Структурные элементы двух семейств у неправильного многоугольника «тетраэдр»
Гипотенузы трех меньших треугольников Кеплера одним своим концом соединены с вершиной тетраэдра, а другим – с центром симметрии тетраэдра. В свою очередь гипотенузы трех больших треугольников Фибоначчи (образующим пары с названными ранее треугольниками Кеплера) одним своим концом соединены с центром симметрии тетраэдра, а другим – с его вершиной (рисунки 1, 2). Образуемые таким образом пары треугольников соприкасаются друг с другом меньшими катетами. Гипотенузы же трех больших треугольников Кеплера соприкасаются с гипотенузами трех больших треугольников Фибоначчи, а гипотенузы трех меньших треугольников Фибоначчи – с меньшими катетами трех больших треугольников Кеплера под прямым углом (рисунки 1, 2).
Рисунок 1 – Неправильный тетраэдр. Сечение неправильного тетраэдра, проходящее через его вершину и центр основания – равносторонний треугольник (сверху). Двумерное изображение большего треугольника Кеплера и меньшего треугольника Фибоначчи (снизу). Треугольник Кеплера обозначен красным цветом, треугольник Фибоначчи – синим 
Рисунок 2 – Неправильный тетраэдр. Вид сверху-сбоку. Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим
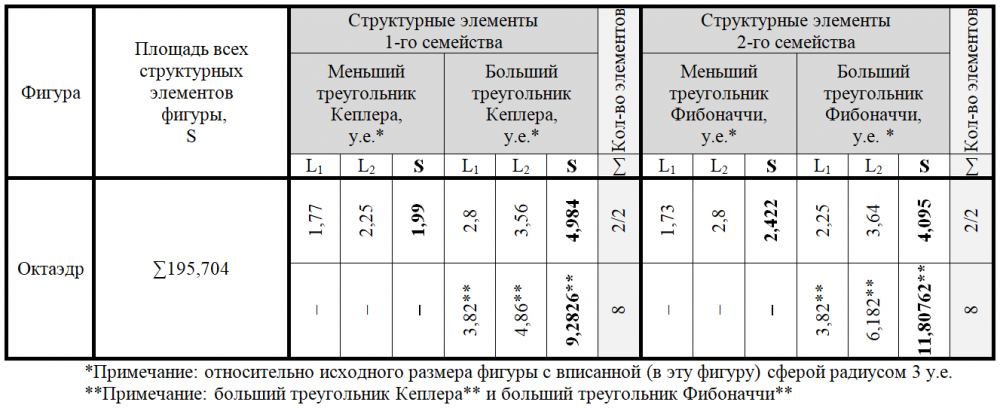
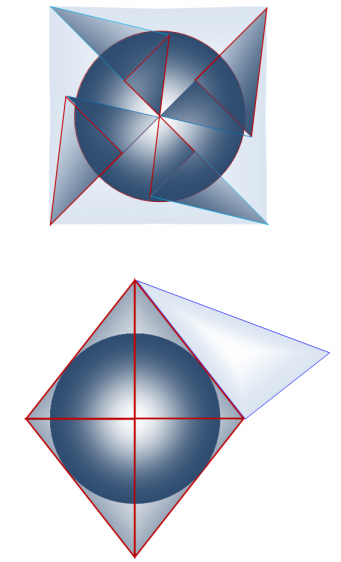
Построение неправильного октаэдра (24 структурных элемента в 12 парах)
Для построения неправильного октаэдра понадобилось 12 пар треугольников Кеплера и Фибоначчи (таблица 3), (рисунки 3, 4). «Каркас» тела формируют 8 больших треугольников Кеплера** соприкасающихся между собой большими катетами в вертикальной плоскости и меньшими – в сагиттальной и горизонтальной плоскостях (крест-накрест) (рисунок 3, снизу). Восемь больших треугольников Фибоначчи** местами соединения гипотенуз и больших катетов образуют две противолежащих вершины тела, а меньшими своими катетами – периметр средней части и четыре вершины тела. Больший катет больших треугольников Фибоначчи** и гипотенузы больших треугольников Кеплера** образуют апофемы двух пирамидальных конструкций геометрического тела. «Внутреннюю» структуру неправильного октаэдра – проекция поперечного сечения в горизонтальной и сагиттальной плоскостях – образуют два меньших и больших треугольника Кеплера, а так же – два меньших и больших треугольника Фибоначчи (рисунок 3, сверху).
Таблица 3 – Структурные элементы двух семейств у неправильного многоугольника «октаэдр» 
Рисунок 3 – Сечение поперечное (сверху) и продольное (снизу) неправильного октаэдра, проходящее через его центр симметрии. Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим 
Рисунок 4 – Неправильный октаэдр. Вид сверху (вверху), вид сбоку (снизу). Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим
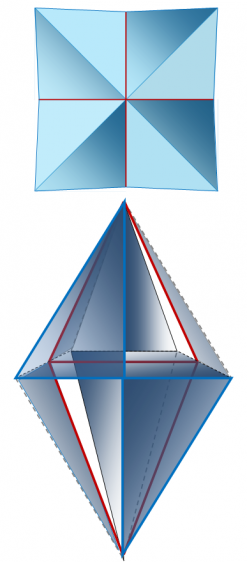
Построение правильного куба (48 структурных элемента в 24 парах)
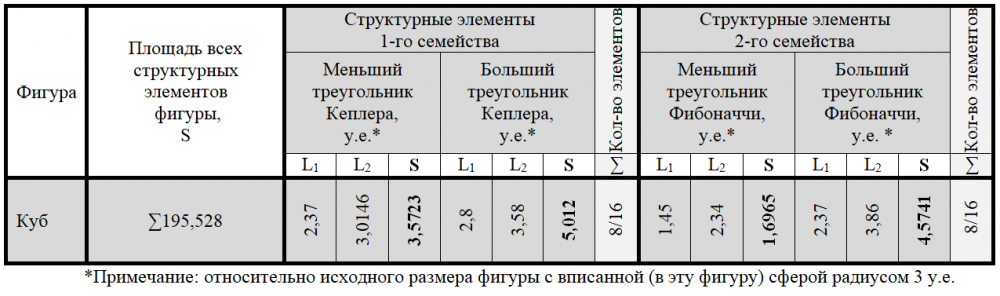
Построение геометрии куба посредством треугольников Кеплера и Фибоначчи требует 24 их пары. На рисунке 5 показано два варианта (из шести подобных этим двум) диагональных сечений куба, каждое из которых проходит через его 4 вершины и центр симметрии.
В первом варианте диагонального сечения куба (первый тип плоскости куба (всего 4 плоскости)) (рисунок 5, сверху) два больших и два меньших треугольников Кеплера соединены в одном случае гипотенузами с 2 большими треугольниками Фибоначчи, а в другом – гипотенузой с большим катетом большего треугольника Фибоначчи. Соединения больших катетов и гипотенуз треугольников Кеплера и Фибоначчи в этом варианте образуют центр симметрии куба.
Во втором варианте диагонального сечения куба (второй тип плоскости куба (всего 2 плоскости)) вершины куба образованы соединением катетов 4 меньших треугольников Фибоначчи, гипотенузы которых являются общими с меньшими катетами 4 больших треугольников Кеплера (рисунок 5, снизу). Соединения больших катетов и гипотенуз треугольников Кеплера в этом варианте образуют центр симметрии куба.
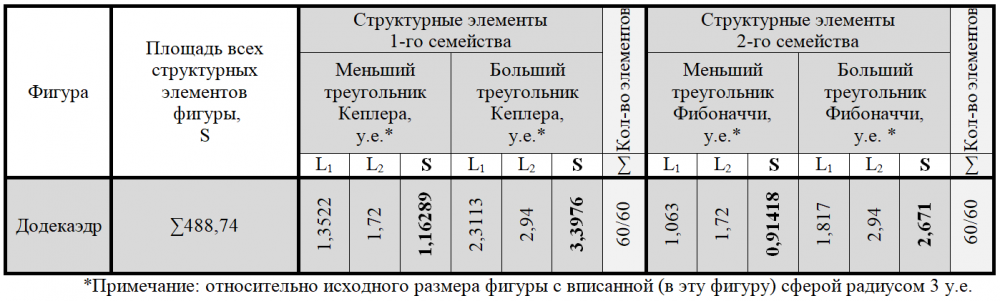
Общее количество структурных элементов куба, их размер (исходного размера фигуры с вписанной в нее сферой радиусом 3 у.е.) и их площадь представлены в таблице 4.
Таблица 4 – Структурные элементы двух семейств у правильного многоугольника «куб» 
Рисунок 5 – Диагональное сечение куба, проходящее через его 4 вершины и центр симметрии. Сверху – первый тип плоскости куба (всего 4 плоскости), снизу – второй тип плоскости куба (всего 2 плоскости). Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим
Для наглядного представления геометрии куба с треугольниками Кеплера и Фибоначчи мы представили рисунок двух диагональных сечений куба второго типа (рисунок 5, снизу) в трехмерной плоскости (рисунок 6). Мы сочли ненужным представление всех шести сечений куба в одном рисунке, так как подобное изображение окажется чрезмерно сложным для восприятия.
Рисунок 6 – Два диагональных сечения куба через его вершины в трехмерной плоскости. Вид сверху-спереди-сбоку. Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим
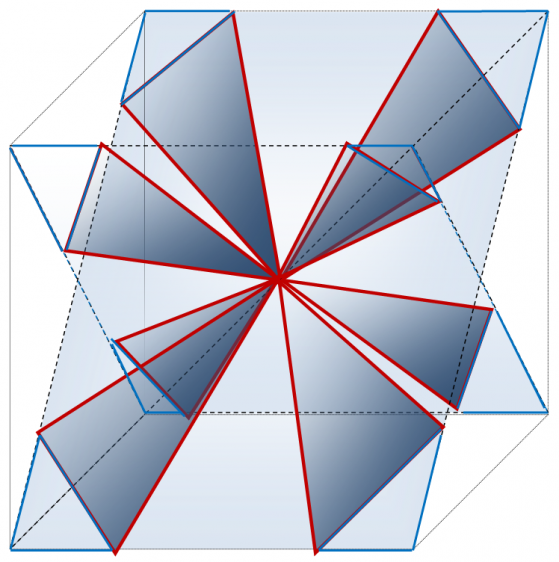
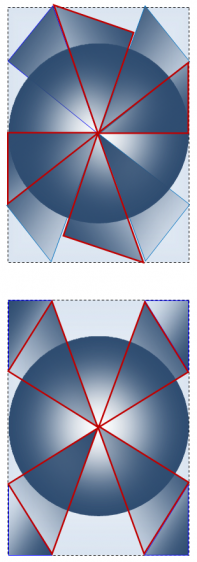
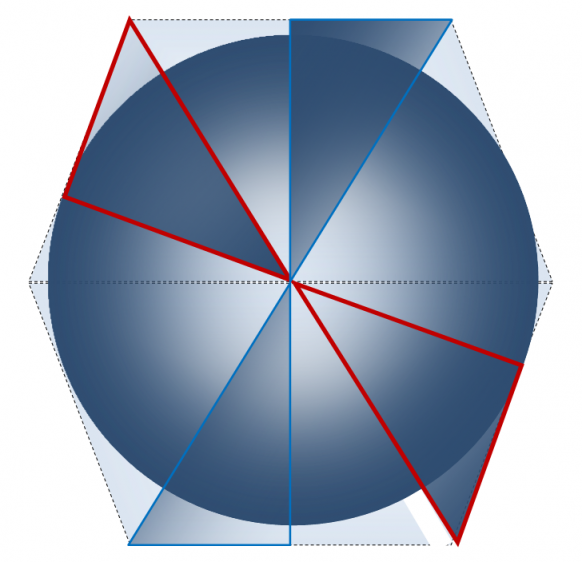
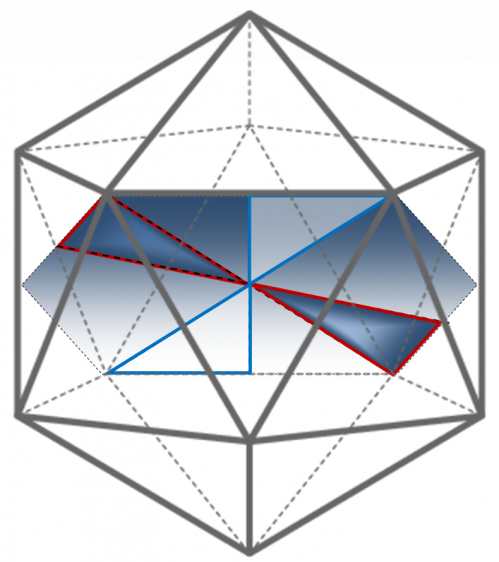
Построение правильного икосаэдра (60 структурных элементов в 30 парах)
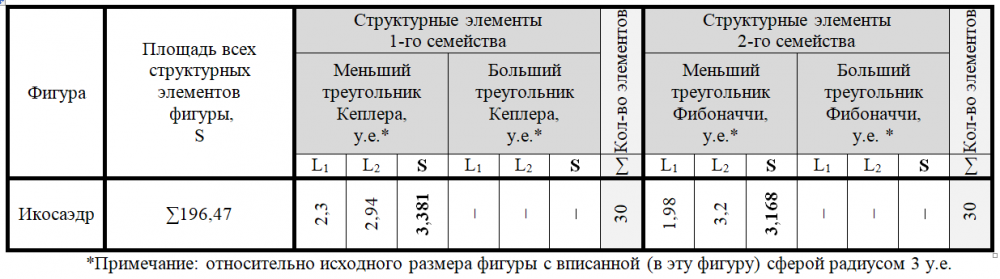
Существует возможность построения икосаэдра из тридцати пар треугольников Кеплера и Фибоначчи. Для наглядности при построении икосаэдра мы воспользовались его поперечным сечением, проходящим через его центр симметрии и четыре противоположных вершины (два ребра) [1] (рисунки 7, 8). Ребра фигуры образованы меньшими катетами треугольников Кеплера и Фибоначчи. Вершины икосаэдра образуют соединения меньшего катета и гипотенузы двух треугольников Кеплера и – двух Фибоначчи (рисунки 7, 8). Центр симметрии икосаэдра находится в месте соединения гипотенуз с большими катетами двух видов треугольников. Икосаэдр содержит 30 ребер, следовательно, рассматриваемых нами сечений в нем – 15. Каждое сечение содержит по 2 пары треугольников Кеплера и Фибоначчи. Общее количество структурных элементов икосаэдра, таким образом, – равно 60 (таблица 5).
Таблица 5 – Структурные элементы двух семейств у правильного многоугольника «икосаэдр» 
Рисунок 7 – Поперечное сечение икосаэдра, проходящее через его центр симметрии и четыре противоположных вершины (два ребра) [1]. Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим 
Рисунок 8 – Сечение икосаэдра в трехмерной плоскости. Вид сверху-спереди. Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим
Построение правильного додекаэдра (240 структурных элементов в 120 парах)
Дуальный икосаэдру додекаэдр можно воспроизвести из 240 треугольников – 60-ти пар треугольников Кеплера и Фибоначчи (таблица 6). На рисунках 9, 10 представлено сечение додекаэдра, проходящее через его центр симметрии и четыре противоположных вершины [1]. Рассматриваемое сечение позволяет разместить в нем четыре пары больших треугольников Кеплера и Фибоначчи с центром симметрии в середине геометрического тела (4*15=60). При этом общими для пар – больших треугольников Кеплера и Фибоначчи – являются их большие катеты. Своими меньшими катетами они образуют линию сечения додекаэдра (его ребра). Меньшие треугольники Кеплера и Фибоначчи образуют грани додекаэдра: каждая из 12 граней фигуры содержит по 5 пар меньших треугольников Кеплера и Фибоначчи (12*5=60). Треугольники пар соприкасаются большими катетами, а меньшими катетами – образуют ребра фигуры (рисунок 9).
Таблица 6 – Структурные элементы двух семейств у правильного многоугольника «додекаэдр» 
Рисунок 9 – Поперечное сечение додекаэдра, проходящее через его центр симметрии и четыре противоположных вершины (два ребра) [1]. Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим 
Рисунок 10 – Сечение додекаэдра в трехмерной плоскости. Вид сверху-спереди. Треугольники Кеплера обозначены красным цветом, треугольники Фибоначчи – синим
Опыт построения платоновых тел (их геометрической структуры из структурных элементов) свидетельствует о возможности создания этих геометрических фигур посредством структурных элементов – треугольников Кеплера и Фибоначчи – при условии неизменности площади названных элементов. Количество элементов (или пар элементов) составляющих структуру «тетраэдра», «октаэдра», «куба» увеличивается, таким образом, в два раза, а «икосаэдра» – в пять раз по отношению к количеству элементов тетраэдра при неизменности показателя «площадь всех структурных элементов фигуры» (таблица 7).
Таблица 7 – Сводная таблица: структурные элементы двух семейств у геометрических объектов – платоновых тел
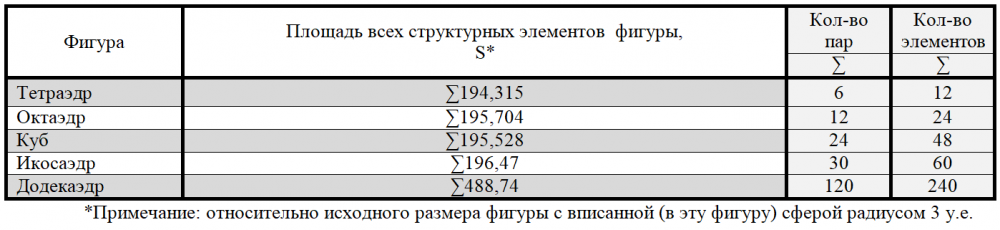
Кроме того, были найдены следующие закономерности при построении платоновых тел посредством элемнтов структуры:
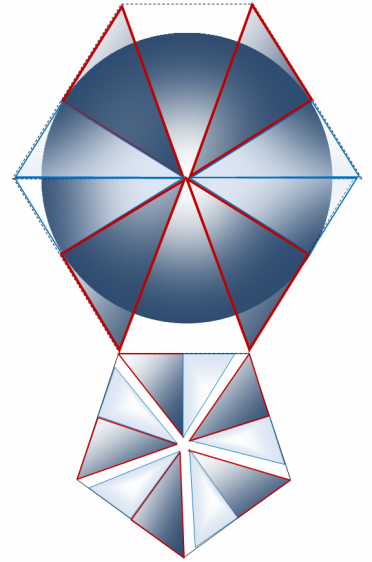
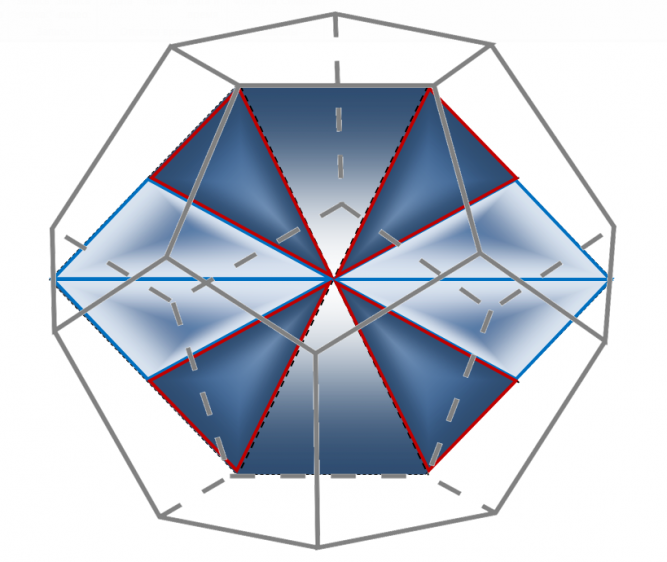
Таким образом: √3*√12791 (√12791=113,0973032392904 – значение площади сферы) = 195,8902754094751=√38 373. Значения числа √38 373 и √12791 соотносятся как 3:1 – это отношение значения площади элементов любого из четырех Платоновых тел (тетраэдра, октаэдра, куба, икосаэдра) к значению площади сферы с радиусом 3. Таким образом: площадь элементов каждого из четырех платоновых тел – тетраэдра, октаэдра, куба, икосаэдра – соотносится к площади (или объему) вписанной в эти четыре тела сферы как √3:1.
Как уже было показано, среди четырех платоновых тел – неправильные тетраэдр и октаэдр, куб, икосаэдр – имеется определенная числовая закономерность: отношение пар треугольников Кеплера и Фибоначчи в определенной нами геометрической структуре этих тел (по порядку их усложнения от тетраэдра, октаэдра и до куба): 6 пар – в тетраэдре, 12 пар – в октаэдре, 24 пары – в кубе, 30 пар в икосаэдре, 120 пар в додекаэдре. Таким образом, если брать за единицу отсчета количество пар додекаэдра (120 пар=240 элементов), то количество этих пар будет кратно количеству элементов 20 тетраэдров, 10 октаэдров, 5 кубов, 4 икосаэдра. В то же время, площадь элементов тетраэдра, октаэдра, куба, икосаэдра одинакова и равна значению √3 помноженное на значение площади вписанной окружности.
Из площади структурных элементов двух додекаэдров (Sc.э.2дод.=√959 325) можно получить площадь равную площади структурных элементов любых 5-ти платоновых тел, например, 5-ти тетраэдров или октаэдров, кубов, икосаэдров… и так далее (Sc.э.пл.т.=√38 373).
Значение площади и тождественное значение объема вписанной в платоновы тела сферы (113,0973032392904) кратно значению меры «Королевский кубит» [3], а получаемое в этом случае кратное значение – 216 (1) – равно значению тождества объема и площади куба (см. таблицу 1) [4].
Высказанное нами предположение о возможности переходов (перерождения) платоновых тел друг в друга (при некоторой постоянной величине (параметре) при прочих переменных) оказалась практически реализуемым при постоянной величине (параметре) «площадь структурных элементов», а в качестве переменной – их кратное количество в «структуре» платоновых тел.
Интерпретация и обсуждение результатов исследования
Учитывая, что описанное математическое тождество площади, объема и одинаковый радиус вписанной окружности наблюдается только у трехмерных фигур – платоновых тел (которые могут быть построены из двух типов треугольников обладающих соотношением меры золотой пропорции) можно предположить (следуя методологическому принципу «Бритва Оккама»), что в качестве универсальных мер Природы, обеспечивающих целостность и соразмерность всех ее систем, могут выступить:
Каким же образом, учитывая вышесказанное, возможно объяснить реальное проявление (реализацию) в физических материальных объектах меры золотой пропорции и тождественности параметров платоновых тел? В дальнейшем обсуждении, чтобы дать более-менее определенный ответ, невозможно (на наш взгляд) обойтись без использования концепций или теорий метафизического характера. Например, теории мировой среды.
Следует отметить, что в произведении Платона «Тимей», где философ излагает свою космологию, слово «правдоподобно» и «правдоподобие» встречается 19 раз. По определению, правдоподобие – сходство с правдой, истиной. И в то же в произведении, в контексте изложения о правдоподобном, встречается часто слово «миф» – 5 раз. Подчеркивается героем повествования, что сказанное специально облачено в форму мифа и оно, по-возможности, соответствует истине в рамках меры правдоподобия: «… мы, рассматривая во многих отношениях много вещей, таких, как Боги и рождение Вселенной, не достигнем в наших рассуждениях полной точности и непротиворечивости. Напротив, мы должны радоваться, если наше рассуждение окажется не менее правдоподобным, чем любое другое, и притом помнить, что и я, рассуждающий, и вы, мои судьи, всего лишь люди, а потому нам приходится довольствоваться в таких вопросах правдоподобным мифом, не требуя большего»; «… у этого сказания облик мифа, но в нем содержится и правда …». Герой произведения поясняет свой выбор изложения в форме правдоподобного мифа следующими доводами: «…при избранном нами способе исследования затруднительно было бы привести наши мысли … в должную ясность. Поэтому ни вы не должны требовать от меня последнего слова на этот счет, ни я не могу убедить себя, что поступлю правильно, если взвалю на себя такую задачу. Напротив, я намерен и здесь придерживаться того, что обещал в самом начале, а именно: пределов вероятного, и попытаюсь, идя от начала, сказать обо всем в отдельности и обо всем вместе такое слово, которое было бы не менее, а более правдоподобным, нежели любое иное» [5]. В этой связи следует воспринимать написанное Платоном в «Тимее» как некое мифическое, но в то же время правдоподобное повествование, в котором существует правдивое знание в форме мифа, сказки…
Что же подразумевалось в «Тимей» под словами «Восприемница» и «Кормилица»? В последующем тексте мы не раз встречаем эти слова во вполне определенном контексте. Вот, к примеру, в таком: «…о Кормилице рождения скажем вот что: поскольку она и растекается влагой, и пламенеет огнем, и принимает формы земли и воздуха, и претерпевает всю чреду подобных состояний, являя многообразный лик, и поскольку наполнявшие ее силы не были ни взаимно подобны, ни взаимно уравновешены и сама она ни в одной своей части не имела равновесия, она повсюду была неравномерно сотрясаема и колеблема этими силами и в свою очередь сама колебала их своим движением. … Вот наподобие этого и четыре упомянутых рода были тогда колеблемы Восприемницей, которая в движении своем являла собой как бы сито: то, что наименее сходно между собой, она разбрасывала дальше всего друг от друга, а то, что более всего сходно, просеивала ближе всего друг к другу; таким образом, четыре рода обособились в пространстве еще до того, как пришло время рождаться устрояемой из них Вселенной» [5].
Из вышесказанного можно предположить, что под словами «Восприемница» и «Кормилица» вероятно подразумевалась мировая среда (эфир), а под платоновыми телами (четыре рода) – наименьшие из элементарных частиц – фундаментальные частицы. Таким образом, платоновы тела (фундаментальные частицы) могут обладать свойством взаимного перехода (перерождения) и некоторым образом – быть связанными с мировой средой (эфиром). Каким же образом может быть обеспечена эта связь? Обратимся в этой связи к высказыванию В.И. Ленина, которое он сделал в своей главной работе по философии «Материализм и эмпириокритицизм. Критические заметки об одной реакционной философии» где указывает: «Как ни диковинно с точки зрения “здравого смысла” превращение невесомого эфира в весомую материю и обратно … – … это только лишнее подтверждение диалектического материализма». Именно от этого высказывания и будем исходить в дальнейших логических построениях.
Итак: платоновы тела (фундаментальные частицы) могут «перерождаться» друг в друга и, в то же время, – непосредственно физически проявляться в результате «превращения» мировой среды (эфира) в материю (частицы). Исходя из существующих модельных представлений о мировой среде [2] (рисунок 11) и выявленных в данном исследовании возможностях взаимного перехода платоновых тел можно наглядно представить появление и взаимный «переход» платоновых тел (рисунок 12). Согласно нашим представлениям – из двух элементов (тел 2 додекаэдров) додекаэдрового поля (составляющего мировую среду) может возникнуть 5 элементов (5 тел) любого из четырех платоновых тел «тетраэдр», «октаэдр», «куб», «икосаэдр».
Рисунок 11 – Модель «додекаэдрового поля»: четыре ракурса 13-ти элементов-додекаэдров «додекаэдрового поля» (фотографии) 
Рисунок 12 – Появление и взаимный «переход» платоновых тел (выпуклых правильных многогранников) и их количественные составляющие – пары элементов
Радиус вписанной сферы в платоновы тела одинаков, а значит – при наличии неизменной величины параметра – можно предположить, что, кроме взаимного «перехода» одного тела в другое возможно и движение тел в среде, названной нами в публикации [2] как «додекаэдровое поле» (мировая среда). На рисунке 13 показана модель «додекаэдрового поля» состоящая из элементов-сфер и вписанных в это «додекаэдровое поле» (см. рисунок 11). Моделирование условий различного расположения сфер у модели додекаэдрового поля показало возможность их подвижности относительно друг друга в двух направлениях – вертикальном (рисунок 13, вверху) и горизонтально-сагиттальном (рисунок 13, внизу). В первом случае соприкасаются радиально расположенные сферы, а во втором – вертикально расположенные.
Рисунок 13 – Модель «додекаэдрового поля»: четыре ракурса 12-ти элементов-сфер вписанных в «додекаэдровое поле» (фотографии)
Предполагаемые способ движения тел в среде додекаэдрового поля – квантовый переход – мгновенное перемещение (квантом движения) вписанных в додекаэдровое поле четырех платоновых тел – «тетраэдр», «октаэдр», «куб», «икосаэдр» – в среде поля. Подобное перемещение, в этом случае, возможно лишь при единичном движении частиц-тел (отдельных фундаментальных частиц) или при условии их объединения в группы со строго определенными композициями, которые позволяют «вписаться» в поле среды.
Возможные композиции частиц-тел (отдельных фундаментальных частиц) представлены моделями платоновых тел (рисунок 14).
Рисунок 14 – Размер платоновых тел с вписанной сферой одинакового радиуса для всех представленных геометрических фигур (фотография)
Нами определены возможные композиции моделей фундаментальных частиц (соединения вершинами фигур, местами граней с совпадением их вершин, местами граней по периметру относительно центра симметрии комплекса фигур):
– икосаэдр+тетраэдр соединены вершинами (рисунок 15, слева);
– октаэдр+тетраэдр соединены вершинами (рисунок 15, справа);
– тетраэдр+тетраэдр соединены гранями (рисунок 16, слева),
– тетраэдр+тетраэдр соединены вершинами (рисунок 16, справа);
– куб+куб… соединены гранями (рисунок 17, слева),
– икосаэдр+икосаэдр… соединены гранями (рисунок 17, справа);
– октаэдр+октаэдр+октаэдр+октаэдр+октаэдр соединены гранями (рисунок 18, слева);
– икосаэдр+икосаэдр+икосаэдр+икосаэдр+икосаэдр соединены гранями (рисунок 18, справа).
Построение различных композиций платоновых тел (в процессе создания моделей фундаментальных частиц в соответствии с «правилам» их нахождения в додекаэдровом поле) позволяет «порождать» значительное разнообразие оригинальных соединений.
Рисунок 15 – Модель фундаментальных частиц: икосаэдр+тетраэдр соединены вершинами (слева), октаэдр+тетраэдр соединены вершинами (справа)(фотографии) 
Рисунок 16 – Модель фундаментальных частиц: тетраэдр+тетраэдр соединены гранями (слева), тетраэдр+тетраэдр соединены вершинами (справа) (фотографии) 
Рисунок 17 – Модель фундаментальных частиц: куб+куб… соединены гранями (слева), икосаэдр+икосаэдр… соединены гранями (справа) (фотографии) 
Рисунок 18 – Модель фундаментальных частиц: октаэдр+октаэдр+октаэдр+октаэдр+октаэдр соединены гранями (слева), икосаэдр+икосаэдр+икосаэдр+икосаэдр+икосаэдр соединены гранями (справа)(фотографии)
Заключение
Список литературы:
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.