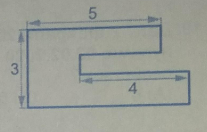
Все углы на рисунке справа прямые чему равен периметр фигуры на рисунке
Все углы на рисунке прямые. Чему равен периметр фигуры на рисунке?
Все углы на рисунке прямые. Чему равен периметр фигуры на рисунке?
Расставим необходимые буквы, перед этим продлив отрезок CD до пересечения с AI.
Так или иначе, все величины, входящие в периметр, мы знаем:
В) 24
Есть шесть карточек с цифрами от 1 до 6 и полоска из шести клеток. Коля, Катя и Маша сели за круглый стол и по очереди (по часовой стрелке), начав с кого-то из них, кладут на пустую клетку полоски по одной карточке. Коля хочет, чтобы полученное шестизначное число было побольше, а девочки — поменьше. Какое число может получиться в результате?
Всего возможно три ситуации:
1. Начинает Коля и далее ходы делают девочки и так далее по кругу.
2. Начинает девочка, затем Коля, затем другая девочка и так далее по кругу.
3. Начинает две девочки, затем Коля и так далее по кругу.
Заполнение полоски будет вестись слева направо, так как в большей мере величину числа определяет старший разряд.
— Коля ставит наибольшую цифру: 6
— девочки ставят по очереди наименьшие цифры из оставшихся: 1 и 2
— Коля ставит наибольшую цифру из оставшихся: 5
— девочки ставят по очереди наименьшие цифры из оставшихся: 3 и 4
Итоговое число 612534
— первая девочка ставит наименьшую цифру: 1
— Коля ставит наибольшую цифру из оставшихся: 6
— девочки ставят по очереди наименьшие цифры из оставшихся: 2 и 3
— Коля ставит наибольшую цифру из оставшихся: 5
— вторая девочка ставит наименьшую цифру из оставшихся: 4
Итоговое число 162354
— девочки ставят по очереди наименьшие цифры из имеющихся: 1 и 2
— Коля ставит наибольшую цифру из оставшихся: 6
— девочки ставят по очереди наименьшие цифры из оставшихся: 3 и 4
— Коля ставит наибольшую цифру из оставшихся: 5
Итоговое число 126345
Таким образом, могли получиться числа: 612534, 162354, 126345.
Из предложенных — это число 162354.
Д) 162354
У кенгуренка Смартика есть восемь кубиков. У каждого кубика две соседние грани красные, а остальные — белые. Смартик сложил из них большой куб 2х2х2. Какое наибольшее количество красных граней может оказаться у большого куба?
У царя Гороха было много детей. В день своего столетия он заявил: У одного из моих детей три брата, а у другого — поровну братьев и сестер. Какое наибольшее количество детей могло быть у царя Гороха?
В гирлянде 5 лампочек горят, а остальные перегорели (см.рисунок). Какое наименьшее число лампочек нужно заменить, чтобы среди любых трёх подряд идущих лампочек хотя-бы две горели?
Математика 1 класс учебник Моро 1 часть страница 97
👉 Ответы на задания к странице 97. Математика 1 класс учебник Моро 1 часть. Моро М. И, Волкова В. С.
✔ Готовое домашнее задание с подробным решением
Задание 1. Задание на полях.
Прямой угол — третье изображение на рисунке.
На рисунке изображены острый угол, тупой угол и прямой угол.
Острый угол — угол, градусная мера которого менее 90 градусов.
Тупой угол — угол, градусная мера которого более 90 градусов.
Прямой угол — угол, градусная мера которого равна 90 градусам.
Задание 2. Задание на полях.
Сколько прямых углов на рисунке домика?
На рисунке домика 8 прямых углов.
Задание 3. Задание под чертой.
Сколько прямых углов в каждом многоугольнике?
В первом многоугольнике нет прямых углов. Только острые.
Во втором многоугольнике 2 прямых угла.
В третьем многоугольнике все углы прямые.
💡 Чтобы не искать ГДЗ к упражнениям в следующий раз сохрани в закладки. Нажми на клавиатуре CTRL + D или поделись в социальных сетях.
Присоединяйтесь к нам!
Получайте уведомления о выходе новых решебников и примите участие в ежемесячном розыгрыше.
Все углы на рисунке прямые. Чему равен периметр фигуры на рисунке (см.)?
Все углы на рисунке прямые. Чему равен периметр фигуры на рисунке?
Получается сумма всех вертикальных сторон фигуры равна 3+3=6.
Рассмотрим самую нижнюю сторону и сопоставим с ней те стороны, длину которых мы уже знаем.
Получается система уравнений:
Решив систему, получаем, что х=1, а у=2.
Длина нижней стороны = 6.
Сумма всех горизонтальных сторон равна 5+3+4+6 = 18.
Чтобы найти периметр фигуры, нужно сложить длину всех сторон. Так как мы уже нашли суммы всех вертикальных и горизонтальных отрезков, остается сложить два числа: 6+18=24
Искомый нами периметр равен 24.
Думаю ответ будет 23, то есть под буквой (б). Решал эту задачу я на глаз, по этому точно ответ сказать не могу. Но если вы сами присмотритесь,то у вас скорее всего будет ответ как у меня. Как говорится глаз-алмаз.
Построим прямоугольник 5*3. Периметр такого прямоугольника равен 16. Из этого периметра надо вычесть ещё некоторое количество, поэтому ответ должен быть ещё меньше 16-ти.
В расчетах придется делать допущения, то есть определять некоторые размеры на глаз. Вычисляем неизвестные размеры, вторая горизонтальная линия сверху, на мой взгляд, равна 3. Самая нижняя линия горизонтальная, так же, на мой взгляд, равна 6.
Суммируем вертикальные линии. Они по любому равны в сумме 6. Горизонтальные линии начиная сверху 5 + 3 + 4 + 6 = 18. Высчитываем общую длину периметра. 6 + 18 = 24.
Предполагаемый мой вариант ответа 24.
Существует определенный алгоритм действий по использованию этого метода. Приведу его здесь:
И конкретный пример расчета:
После этого все цифры, которые мы получили плюс все цифры даты рождения: 22081987 размещаем в девяти ячейках квадрата Пифагора (3Х3): все единицы в первом квадратике, двойки во втором и т.д. И анализируем их. Анализ каждой цифры будет зависеть от того, сколько одинаковых цифр в каждом квадрате. Анализ можно посмотреть тут.
Вычитанием называется двухместная операция, обратная сложению. Она не коммутативна и не ассоциативна, обладает антикоммутативностью. В случае, если на том же множестве определено ещё и умножение, то вычитание должно быть дистрибутивно по отношению к нему.
То есть, в арифметике у вычитания выделяют лишь 2 свойства:
Ассоциативность и привычная по сложению коммутативность отсутствуют:
Итак, к середине первого месяца Яков должен был банку (1+b/100)*60000 рублей. К концу месяца после первого гашения долга осталась сумма ((1+b/100)*60000-12900) рублей.
К середине следующего месяца долг составил (1+b/100)*((1+b/100)*60000- 12900) рублей, что в соответствии с условиями равно 52605 рублям.
Таким образом, получаем квадратное уравнение 6b^2+1071b-5505=0, единственным положительным корнем которого является b=5, то есть процентная ставка равна 5%.
У умножения есть переместительное, сочетательное и распределительное свойство (которые чаше называются законами). Записываются они так (в том же порядке):
Могу посоветовать сайт, которым пользуемся мы, когда ищем ответы по математике. Он называется слово, потом точка, потом домен ws (а не ru).
Там постранично отсканирован решебник, просто и понятно изложено. Вот выдержка именно из него:
Там есть и другие решебники, пригодятся ребенку позже.
Есть еще математикус.ру.
Есть сайт алленг.ру, там можно помимо готовых домашних заданий найти учебники (в том числе и для высшего и средне-профессионального образования), их количество постоянно пополняется.
ПОВТОРЯЕМ ТЕОРИЮ
154. Заполните пропуски.
РЕШАЕМ ЗАДАЧИ
155. На рисунке изображены четырехугольники. Запишите: 1) прямоугольники; 2) квадраты.
156. Периметр квадрата со стороной 6 см равен 24 см.
157. Периметр прямоугольника со сторонами 4 см и 8 см равен 24 см.
Решение:
1) 20:2=10 (см)
2) 10-6=4 (см) другая сторона прямоугольника
159. Из проволоки сделали квадрат со сторой 16 см. Можно ли было из этого куска проволоки сделать прямоугольник со сторонами: 1) 18 см и 14 см; 2) 12 см и 22 см?
Решение:
1) 16*4=64 (см) длина проволоки
2) 2*(18+14)=64 (см) периметр первого прямоугольника
3) 2*(12+22)=68 (см) периметр второго прямоугольника
Ответ: 1) можно; 2) нельзя.
160. Треугольник и квадрат, имеющие равные периметры, расположены так, как показано на рисунке. Сторона квадрата равна 6 см. Чему равен периметр многоугольника, образованного данными треугольником и квадратом?
Ответ: периметр многоугольника равен 36 см.
161. Дострой фигуру, изображенную на рисунке, так, чтобы получилась фигура, для которой прямая а является осью симметрии.
Решение:
2*(200:4+120:4) = 2*(50+30) = 160 м.
Ответ: периметр игровой площадки равен 160 м.
163. Прямоугольный лист бумаги разделили на две части одним прямолинейным разрезом. Какую из перечисленных фигур нельзя получить после разрезания: 1) квадрат; 2) пятиугольник; 3) шестиугольник; 4) прямоугольный треугольник?
164. На рисунке изображен прямоугольник, разбитый на 7 квадратов. Сторона каждого закрашенного квадрата равна 8 см. Чему равна сторона наибольшего квадрата?
165. Разделите квадрат на четыре равные части, проводя линии деления по сторонам клеток так, чтобы в каждой части было по одному кружку.