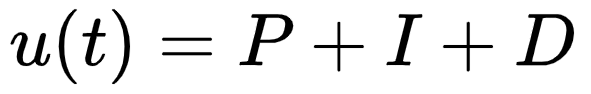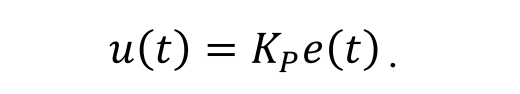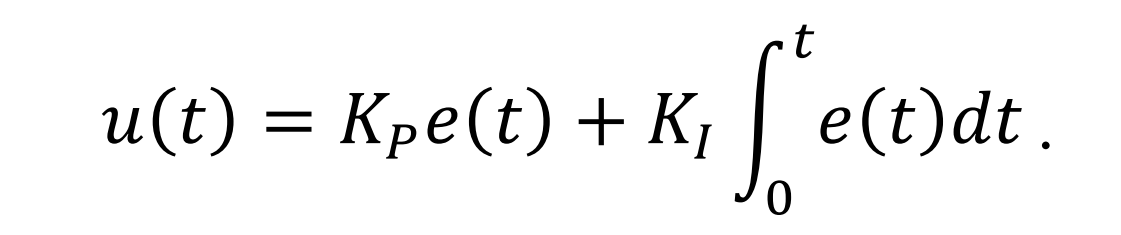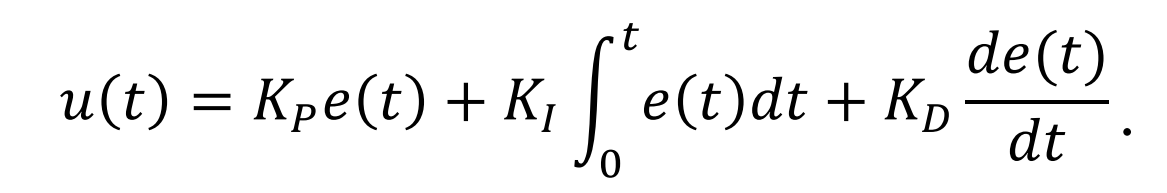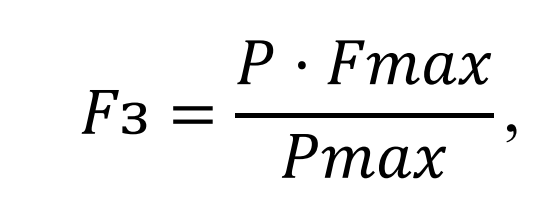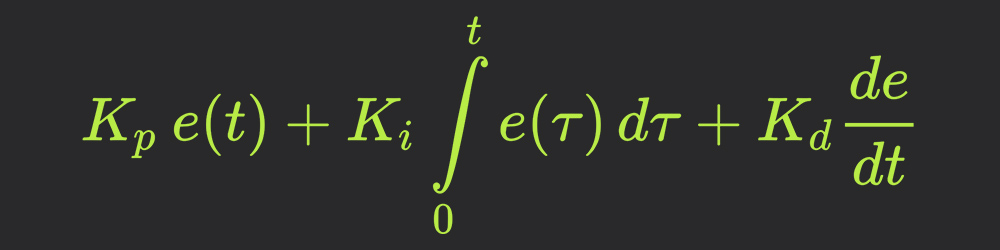Встроенный пид регулятор что это
Что такое ПИД-регулятор
ПИД (от англ. P-proportional, I-integral, D-derivative) — регулятором называется устройство, применяемое в контурах управления, оснащенных звеном обратной связи. Данные регуляторы используют для формирования сигнала управления в автоматических системах, где необходимо достичь высоких требований к качеству и точности переходных процессов.
Управляющий сигнал ПИД-регулятора получается в результате сложения трех составляющих: первая пропорциональна величине сигнала рассогласования, вторая — интегралу сигнала рассогласования, третья — его производной. Если какой-то из этих трех компонентов не включен в процесс сложения, то регулятор будет уже не ПИД, а просто пропорциональным, пропорционально-дифференцирующим или пропорционально-интегрирующим.
Первый компонент — пропорциональный
Выходной сигнал дает пропорциональная составляющая. Сигнал этот приводит к противодействию текущему отклонению входной величины, подлежащей регулированию, от установленного значения. Чем больше отклонение — тем больше и сигнал. Когда на входе значение регулируемой величины равно заданному, то выходной сигнал становится равным нулю.
Если оставить только эту пропорциональную составляющую, и использовать только ее, то значение величины, подлежащей регулированию, не стабилизируется на правильном значении никогда. Всегда есть статическая ошибка, равная такому значению отклонения регулируемой величины, что выходной сигнал стабилизируется на этом значении.
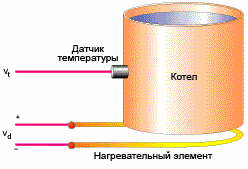
К примеру, терморегулятор управляет мощностью нагревательного прибора. Выходной сигнал уменьшается по мере приближения требуемой температуры объекта, и сигнал управления стабилизирует мощность на уровне тепловых потерь. В итоге заданного значения температура так и не достигнет, ибо нагревательный прибор в просто должен будет быть выключен, и начнет остывать (мощность равна нулю).
Больше коэффициент усиления между входом и выходом — меньше статическая ошибка, но если коэффициент усиления (по сути — коэффициент пропорциональности) будет слишком большим, то при условии наличия задержек в системе (а они зачастую неизбежны), в ней вскоре начнутся автоколебания, а если увеличить коэффициент еще больше — система попросту утратит устойчивость.
Или пример позиционирования двигателя с редуктором. При малом коэффициенте нужное положение рабочего органа достигается слишком медленно. Увеличить коэффициент — реакция получится более быстрая. Но если увеличивать коэффициент дальше, то двигатель «перелетит» правильную позицию, и система не перейдет быстро к требуемому положению, как хотелось бы ожидать. Если теперь увеличивать коэффициент пропорциональности дальше, то начнутся осцилляции около нужной точки — результат снова не будет достигнут.
Интеграл по времени от величины рассогласования — есть основная часть интегрирующей составляющей. Она пропорциональна этому интегралу. Интегрирующий компонент используется как раз для исключения статической ошибки, поскольку регулятор со временем учитывает статическую погрешность.
В отсутствие внешних возмущений, через какое-то время подлежащая регулированию величина будет стабилизирована на правильном значении, когда пропорциональная составляющая окажется равной нулю, и точность выхода будет целиком обеспечена интегрирующей составляющей. Но интегрирующая составляющая тоже может породить осцилляции около точки позиционирования, если коэффициент не подобран правильно.
Третий компонент — дифференцирующий
Темпу изменения отклонения величины, подлежащей регулированию, пропорциональна третья — дифференцирующая составляющая. Она необходима для того, чтобы противодействовать отклонениям (вызванным внешними воздействиями или задержками) от правильного положения, прогнозируемого в будущем.
Что такое ПИД простыми словами на примере дрона:
Теория работы ПИД-регулятора
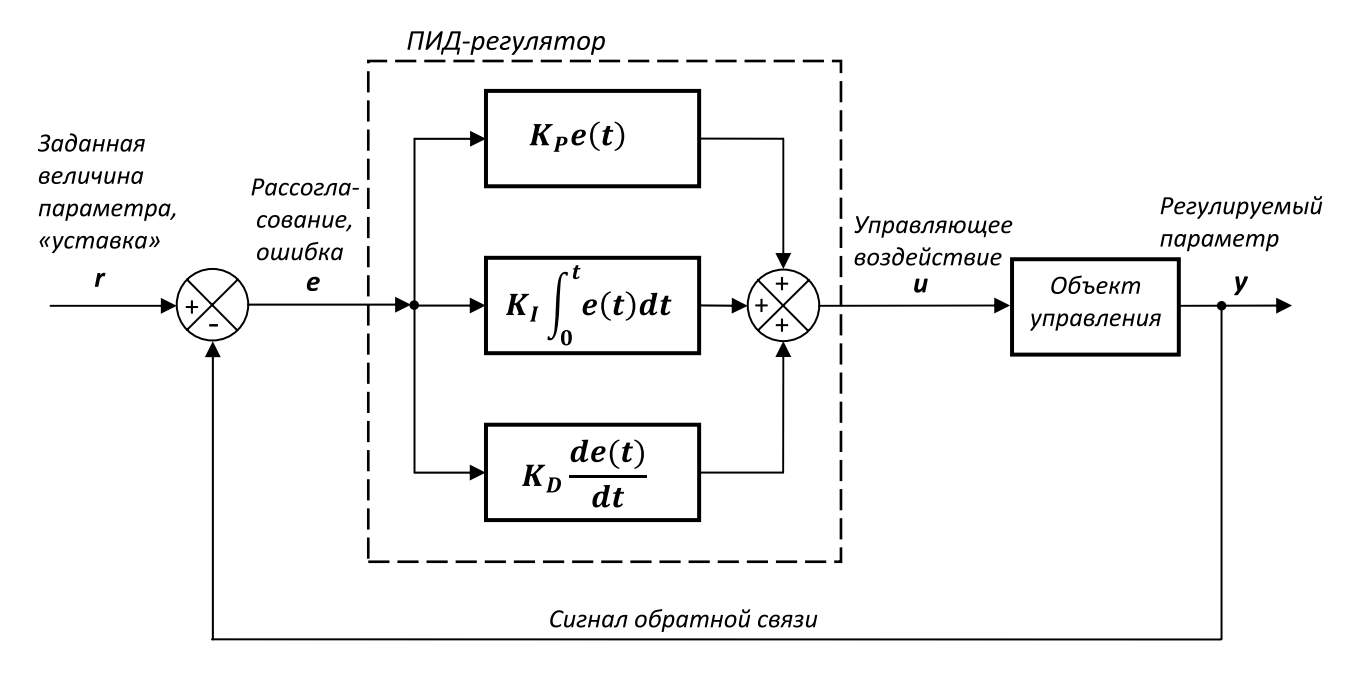
Как вы уже поняли, ПИД-регуляторы применяют для поддержания заданного значения х0 некоторой одной величины, благодаря изменению значения u другой величины. Есть уставка или заданное значение х0, и есть разность или невязка (рассогласование) е = х0-х. Если система линейна и стационарна (практически это вряд ли возможно), то для задания u справедливы нижеследующие формулы:
В этой формуле вы видите коэффициенты пропорциональности для каждого из трех слагаемых.
Практически в ПИД-регуляторах используют для настройки другую формулу, где коэффициент усиления применен сразу ко всем компонентам:
Практическая сторона ПИД-регулирования
Практически теоретический анализ ПИД-регулируемых систем редко применяют. Сложность состоит в том, что характеристики объекта управления неизвестны, и система практически всегда нестационарна и нелинейна.
Реально работающие ПИД-регуляторы всегда имеют ограничение рабочего диапазона снизу и сверху, это принципиально объясняет их нелинейность. Настройка поэтому практически всегда и везде производится экспериментальным путем, когда объект управления подключен к системе управления.
Использование величины, формируемой программным алгоритмом управления, обладает рядом специфических нюансов. Если речь, например, о регулировке температуры, то часто требуется все же не одно, а сразу два устройства: первое управляет нагревом, второе — охлаждением. Первое подает разогретый теплоноситель, второе — хладагент. Три варианта практических решений может быть рассмотрено.
Сегодня системы автоматизации практически все строятся на основе ПЛК, и ПИД-регуляторы представляют собой специальные модули, добавляемые к управляющему контроллеру или вообще реализуемые программно путем загрузки библиотек. Для правильной настройки коэффициентов усиления в таких контроллерах, их разработчики предоставляют специальное ПО.
Structured Text
Книга «Изучаем Structured Text МЭК 61131-3»: Ссылка на книгу
ПИД-регуляторы в частотных преобразователях «Веспер» — высокая точность процесса автоматического регулирования
Преобразователи частоты, как устройства управления асинхронными электродвигателями, — электронные приборы на базе микропроцессорных устройств со своим уникальным программным обеспечением. Они заметно улучшают работу
электропривода и, благодаря встроенному программному модулю «ПИД- регулятор», позволяют оптимизировать работу частотно-регулируемого электропривода в режиме автоматического регулирования параметров технологических процессов.
Благодаря продуманному интерфейсу и упорядоченной структуре меню специалист любого уровня сможет запустить ПЧ «Веспер». Но, чтобы уйти от типичных ошибок при интеграции ПЧ в систему автоматического регулирования, необходимо ознакомиться с принципами работы ПИД-регуляторов и этапами настройки.
Принцип работы ПИД- регулятора
Принцип пропорционально-интегрально-дифференциального (ПИД) регулирования основан на формировании управляющего сигнала, являющегося суммой трёх слагаемых (составляющих):
Эти составляющие формируются соответствующими блоками программного модуля ПИД-регулятора.
ПИД регулятор на базе микропроцессорных устройств, как и любая система автоматического регулирования с обратной связью, предусматривает наличие двух входов и одного выхода: вход сигнала обратной связи с датчика технологического параметра и вход сигнала задания требуемой величины технологического параметра. Выходной сигнал ПИД-регулятора формируется на программном уровне в результате математических вычислений с тремя слагаемыми (P, I, D):
Структура ПИД-регулятора — основные особенности
Контур П-регулятора.
Коэффициент (KP) задаётся численным значением параметра пропорциональной составляющей.
Контур ПИ-регулятора
Чтобы повысить точность (скомпенсировать статическую ошибку) и стабилизировать систему, в структуру вводится программный блок интегральной составляющей (I)
Интегральная составляющая вычисляется по формуле:
т. е. пропорциональна интегралу по времени от отклонения регулируемой величины. Она позволяет регулятору со временем учесть статическую ошибку регулирования и устранить её.
Если система не испытывает внешних возмущений, то через некоторое время значение технологического параметра стабилизируется на заданном уровне, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечиваться интегральной составляющей. Тем не менее, интегральная составляющая также может приводить к автоколебаниям при неправильном выборе её коэффициента.
Таким образом, если использовать два программных блока — пропорциональный и интегральный, то точность процесса регулирования, а соответственно и точность поддержания значения технологического параметра значительно повысится. Степень компенсации статической ошибки регулирования прямо пропорциональна значению коэффициента пропорциональности Ki. Но чем он выше, тем медленнее будут протекать переходные процессы: при очередном запуске системы и при внешних возмущениях. ПИ-регулятор подходит для систем автоматического регулирования, где не важна скорость её реакции. В большинстве случаев для решения задач в замкнутых системах автоматического регулирования вполне достаточно использовать только ПИД- регулятор.
Контур ПИД-регулятора
Чтобы ускорить переходный процесс и еще больше стабилизировать систему, вводится программный блок дифференциальной составляющей. Результирующее значение вычисляется по формуле:
Дифференциальная составляющая пропорциональна скорости изменения отклонения текущего значения технологического параметра от заданного и предназначена для компенсирования подобных отклонений, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему автоматического регулирования.
Задействовать сразу три контура (P + I + D) особенно важно при необходимости увеличения быстродействия системы автоматического регулирования. ПИД-регулирование частотного преобразователя будет наиболее полезно в высокодинамичных системах, когда требуется высокая точность, стабильность и скорость управляющего сигнала. Дифференциальный канал чувствителен к ВЧ-помехам. Поэтому, при построении системы регулирования, необходимо принять меры для защиты от помех.
Преобразователь частоты в системе автоматического регулирования
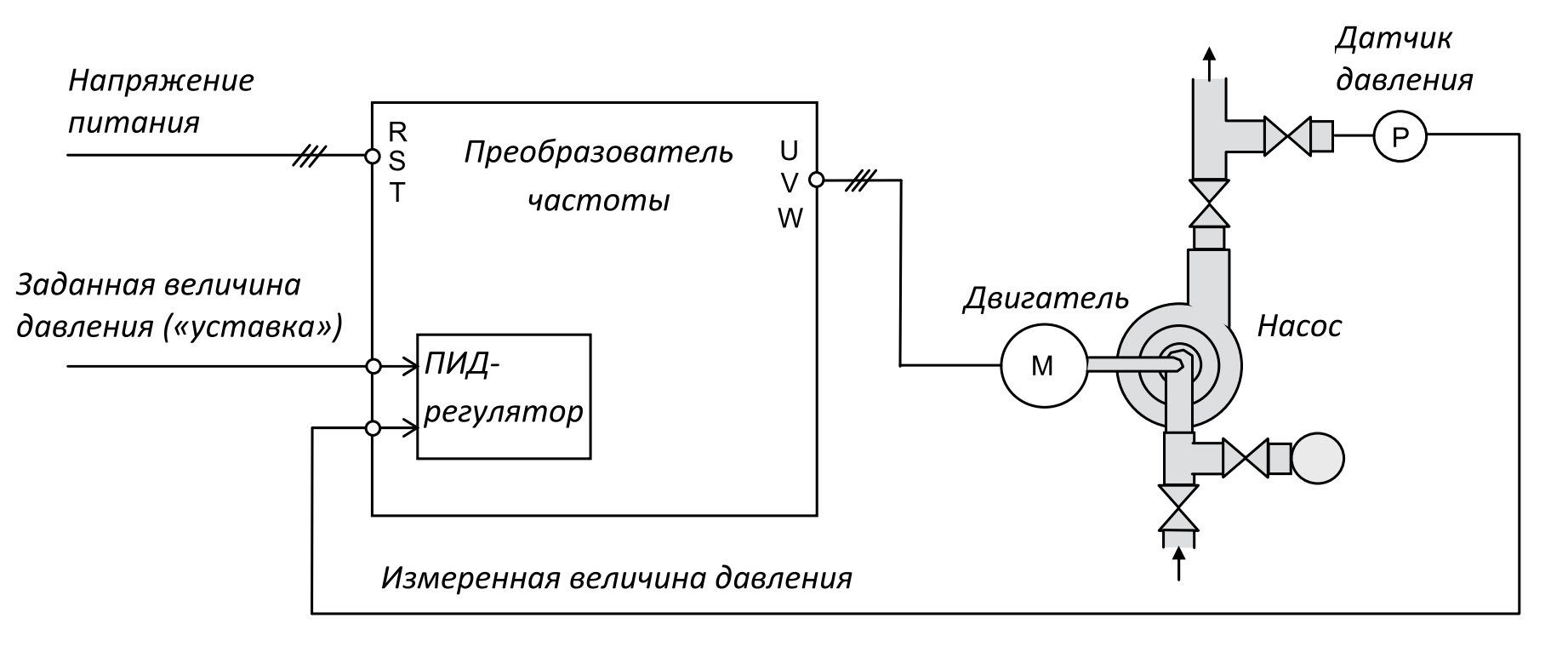
Преобразователи частоты (далее ПЧ) с программным модулем «ПИД-регулятор» универсальны в применении, но особой популярностью они пользуются в гидравлических системах для поддержания постоянного давления жидкости вне зависимости от её расхода.
Типичное решение с применением ПЧ в режиме ПИД-регулирования для поддержания постоянного давления в напорном трубопроводе строится по следующему принципу:
Т.О. давление в напорном трубопроводе останется на заданном уровне и не будет зависеть от расхода.
Пусконаладка ПЧ «Веспер» в режиме ПИД-регулирования
Процесс настройки ПИД-регулятора состоит из нескольких этапов. В целом схема управления типична и состоит в основном из задания уставки и настройки оптимальных значений трех ПИД-коэффициентов.
Уставка (необходимый уровень давления для гидравлических систем) задается путем указания частоты. Показатели частоты вычисляются по формуле:
где FЗ — задание частоты, Гц;
P — необходимое давление в системе, бар;
Fmax — частота электросети на выходе, Гц;
Pmax — верхний диапазон чувствительности датчика, бар.
Для вычисления коэффициентов ПИД-регулятора применяются формулы, но на практике провести точный расчет всех этих значений крайне сложно. Вычислениям мешает нелинейность и нестационарность системы, отсутствие точных характеристик объекта управления. Поэтому настройку ПИД-регулятора частотного преобразователя зачастую проводят с использованием эмпирического и эвристического методов. Оптимальные значения подбираются опытным путем.
Также при настройке ПЧ необходимо указать параметры электропривода: номинальный ток, номинальное напряжение и прочие характеристики, необходимые для корректной работы ПЧ и всей системы автоматического регулирования в целом.
Подробные инструкции по настройке даны в технической документации к каждой модели ПЧ «Веспер». Можно запросить помощь по проведению пусконаладочных работ у технических специалистов компании ВЕСПЕР.
ПИД регулятор
ПИД регулятор – один из самых распространенных автоматических регуляторов. Он настолько универсален, что применяется практически везде, где нужно автоматическое управление. Например температурой: специальные печи, холодильники, инкубаторы, паяльники, сопло и стол 3D принтера, ИК паяльные станции и прочее. Поддержание частоты оборотов мотора, например для станков. Всевозможные балансирующие штуки, гироскутеры, сигвеи, левитирующие магнитные платформы, и конечно же квадрокоптеры и самолёты с автопилотом. Это всё ПИД регулятор. Почему именно ПИД? Существуют и другие регуляторы, превосходящие ПИД по адаптивности к управляемой системе и стабильности, например линейно квадратичный. Но, чтобы грамотно синтезировать такой регулятор, нужно быть гораздо больше чем “семи пядей” во лбу, а настройка ПИД регулятора дело хоть и неприятное, но фактически очень простое и под силу любому, а сам ПИД регулятор универсален для почти любого процесса.
Система управления
Прежде чем переходить непосредственно к пиду, очень важно понять и запомнить несколько базовых понятий, из которых состоит автоматическая система. В первую очередь это регулятор, который всем заправляет и находится в центре системы. Регулятор в данном понимании – математический алгоритм или часть программы, которая крутится на микроконтроллере. Регулятор, как алгоритм, работает с обычными числами. Объект управления – это девайс, которым мы управляем, например печка или мотор. Для этого у нас есть управляющее устройство, например диммируемый тен или драйвер мотора. Управляющее устройство получает от регулятора управляющий сигнал, то есть конкретное число. Это может быть заполнение шим сигнала, от 0 до 255, а может быть угол поворота сервомашинки от 0 до 180, потому что регулятору без разницы чем управлять. В объекте управления у нас стоит датчик, с которого регулятор получает управляемую величину, то есть текущий сигнал с датчика. Это – обратная связь, которая и даёт возможность системе ирчно поддержать заданное значение. В случае с печкой это температура, а с мотором – частота оборотов. Ну и наконец регулятор получает установку (уставку), то есть число, к которому он должен привести текущее значение с датчика. Установка может задаваться каким угодно образом: крутилкой, ползунком, энкодером, кнопками, да хоть смской или голосовым вводом. Регулятору это неважно, для него это просто цифра. Задача регулятора состоит в том, чтобы сравнивать текущее значение с установкой и выдавать управляющий сигнал на управляющее устройство. То есть в программе это будет выглядеть условно так: регулятор получил установку, регулятор получил значение с датчика, регулятор выполнил вычисления и выдал нам управляющий сигнал, опять же число. Если это шим – мы его подаём через функцию генерации шим. Есть ещё один момент – регулятор должен делать расчёты и применять управляющий сигнал через равные промежутки времени, то есть с равным периодом или частотой. Эта частота называется частотой дискретизации системы, а период обозначается как dt, прямо как период интегрирования.
Под капотом у ПИД регулятора
ПИД регулятор состоит из трёх составляющих: пропорциональной P, интегрирующей I и дифференциирующей D, формируется просто как сумма трёх значений, умноженных каждая на свой коэффициент. Эта сумма после вычислений становится управляющим сигналом, который подаётся на управляющее устройство, обозначим его как out.
kP, kI и kD это и есть те самые коэффициенты, которые нужно настроить для работы ПИДа. Значения тут могут быть самые разные, от 0.001 то десятков и тысяч, это зависит от конкретной системы. Тут есть ещё один момент: любой коэффициент может быть равен нулю, и в таком случае обнуляется вся его компонента. То есть регулятор можно превратить в П, ПИ, ПД, и прочие сочетания. Разные системы требуют разного подхода, именно поэтому ПИД регулятор такой универсальный. В дальнейшем будем пользоваться следующими названиями переменных:
P составляющая
Пропорциональная составляющая предоставляет собой разность текущего значения с датчика и установки.
Данная разность называется ошибкой регулирования, то есть насколько далеко находится система от заданного значения. Получается чем больше ошибка, тем больше будет управляющий сигнал и тем быстрее система будет приводить управляемую величину к заданному значению. Коэффициент kP тут влияет роль усиления ошибки и настраивается вручную. Но в то же время, если система пришла к заданной величине, ошибка станет равной нулю, и управляющий сигнал тоже! Другими словами, п регулятор никогда не сможет привести к заданному значению, всегда будет некая ошибка. П составляющая является основной в ПИД регуляторе и так сказать тянет самую большую лямку, регулятор может неплохо работать только лишь на ней одной. P составляющая исправляет ошибку в текущий момент времени.
I составляющая
Интегральная составляющая просто суммирует в саму себя ту же самую ошибку, разность текущего и заданного значения, умноженную на период дискретизации системы, то есть на время, прошедшее с предыдущего расчёта dt – фактически берёт интеграл от ошибки по времени.
В самом регуляторе это ещё умножается на коэффициент kI, которым настраивается резкость данной составляющей. В интегральной составляющей буквально копится ошибка, что позволяет регулятору с течением времени полностью её устранить, то есть привести систему ровно к заданному значению с максимальной точностью. I составляющая исправляет прошлые, накопившиеся ошибки.
D составляющая
Дифференциальная составляющая представляет собой разность текущей и предыдущей ошибки, поделенную на время между измерениями, то есть на ту же dt, которая общий период регулятора. Иными словами – это производная от ошибки по времени.
Фактически D составляющая реагирует на изменение сигнала с датчика, и чем сильнее происходит это изменение, тем большее значение прибавляется к общей сумме. Иными словами, D позволяет компенсировать резкие изменения в системе и при правильной настройке предотвратить сильное перерегулирование и уменьшить раскачку. Коэффициент д позволяет настроить вес, или резкость данной компенсации, как и остальные коэффициенты регулируют свои составляющие. D составляющая в первую очередь нужна для быстрых систем, то есть для систем с резкими изменениями, такие как квадрокоптер или шпиндель станка под переменной нагрузкой. D составляющая исправляет возможные будущие ошибки, анализируя скорость.
Настройка регулятора
Для настройки регулятора нужно варьировать коэффициенты:
Вот так выглядит процесс стабилизации при изменении коэффициентов: 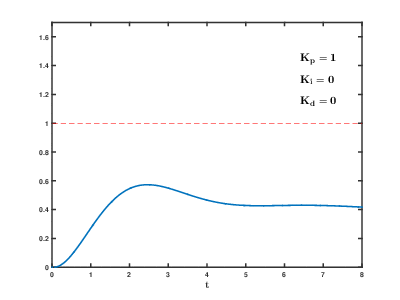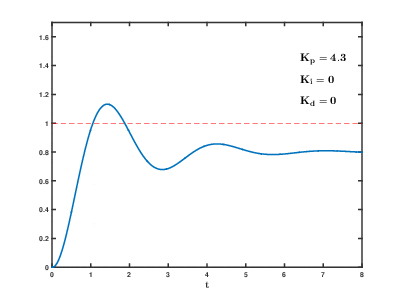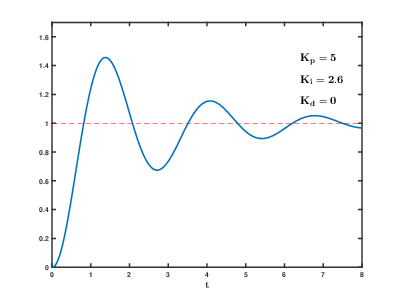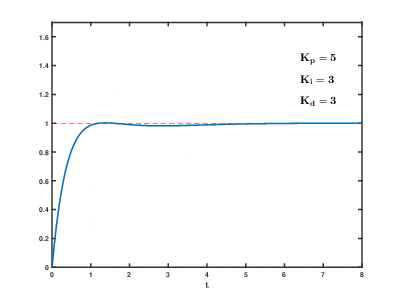
Например, незатухающие колебания появились при kP 20, период колебаний составил 3 секунды. Период dt в системе будет 50 мс (0.05 с). Считаем:
На полученных коэффициентах должны более-менее работать большинство систем, но не все. Также можно воспользоваться автоматическим тюнером коэффициентов, например два разных алгоритма встроены в библиотеку GyverPID.
Реализация на C++
Соединяя все рассмотренные выше уравнения, получим:
Это готовая функция, которая принимает значение с датчика, установку, три коэффициента и время, а также ограничение выхода с регулятора. Как пользоваться этой функцией: функция должна вызываться с некоторым периодом, причем длительность этого периода нужно будет передать в функцию в секундах. Если попроще, можно использовать задержку. Но делать так не рекомендуется, лучше сделать таймер на миллис и работать с ним. Функция возвращает управляющий сигнал, то есть можно подать его например как ШИМ. Период dt имеет такой смысл: чем инерционнее у нас система, тем реже можно вычислять пид. Например для обогрева комнаты период можно поставить 1 секунду или больше, а для контроля за оборотами двигателя надо будет поставить пару десятков миллисекунд, то есть около сотни раз в секунду.
Видео
ПИД-регулятор своими руками
I. Постановка задачи
II. Теоретическая вводная
Как получается ПИД-регулятор? Берём разницу между текущей температурой и нужной, умножаем на настраиваемый коэффициент, получаем мощность, которую надо выдать в данный момент. Это пропорциональная составляющая, она работает в момент появления рассогласования — то есть моментально откликается как на изменение уставки, так и на поведение объекта. Начал подогреваться? Мощность начинает спадать. Перегрелся? Выключилось, или даже дали сигнал охлаждения. Всё хорошо, вот только в реальной жизни эффект от воздействия проявляется с запаздыванием, а на объект воздействуем не только мы, но еще и окружающая среда: разогретый реактор не только внутри горячий, но еще и остывает, отдавая тепло комнате, а потому как только выключаем мощность, он сразу начинает остывать. Поэтому чистый пропорциональный регулятор колеблется вокруг точки поддержания, и тем сильнее колеблется, чем выше воздействие окружающей среды / содержимого реактора.
Чтобы компенсировать «внешние» воздействия на реактор, в цепь добавляют интегральную составляющую. Всё рассогласование, которое было в системе, идёт на интегратор (соответственно, как только мы перегрели — сумма уменьшается, пока недогрето — сумма увеличивается). И накопленный интеграл, со своим коэффициентом, даёт свою прибавку-убавку к мощности. В результате такого подхода, при стационарном процессе, через некоторое время интеграл подбирает такой вклад в сумму с мощностью, который компенсирует потери окружающей среды, и колебания исчезают — интеграл становится стабильным, поэтому величина выдаваемой мощности становится постоянной. Причем так как при этом держится нужная температура, рассогласование отсутствует, пропорциональная составляющая не работает вообще.
Для компенсации влияния задержек между воздействием и реакцией системы, в систему добавляют дифференциальную составляющую. Просто пропорциональный регулятор даёт мощность всё время, пока температура не достигнет нужной точки, пропорционально-дифференциальный начинает снижать подаваемую мощность раньше, чем догрелся до нужной точки — так как рассогласование уменьшается, имеется наличие отрицательной производной, уменьшающей воздействие. Это позволяет минимизировать перегрев при больших переходах.
Итак, с физическим смыслом разобрались, перейдём к основым вопросам реализации.
III. Кому пользоваться регулятором?
Что из этого следует? Из этого следует, что техники понимают физическую составляющую, и имеют опыт настройки аппаратных пид регуляторов. А значит, программная реализация должна исходить из удобства настройки техниками — повторяя физическую модель. И это крайне важно! Очень часто в угоду упрощения кода коэффициенты меняют, например, на обратные — чтобы избавиться от деления. В результате, настройка превращается в ад и кошмар, и требуется опыт настройки данного конкретного регулятора, вместо понимания процесса. Отсюда получаем, что наши коэффициенты — постоянная интегрирования и постоянная дифференцирования — должны иметь размерность времени, то есть задаваться в секундах, а никак не в «1/с», как это любят делать.
IV. Область функционирования.
1200°C, управляется только подача мощности.
Точность управления определяется во-1х точностью измерения: градуировочные таблицы даны через 0.1 градуса; линейность внутри таблиц в принципе достойная, поэтому точность ограничена в первую очередь усилителем и измерителем тока. В моём случае, хотелось добиться точности поддержания 0.1 градуса, поэтому измеритель настроен на 1/32 градуса: это даёт
V. Диапазон настраиваемости.
Для управления микрореактором с мощной силовой установкой может оказаться что для нагрева на 10 градусов достаточно 1% мощности, в то время как для большой инертной печи для того чтобы подогреть на градус едва-едва хватает 100% мощности подогрева. (В реальной жизни, это выглядит так — есть несколько подогревателей с ручным управлением — они включаются отдельным рубильником и производят начальный нагрев, в дальнейшем поддержание рабочей точки обеспечивает терморегулятор, управляя еще одним подогревателем, который на полной мощности выдаёт максимум +10°C к тому, что нагрели постоянно включенные). Исходя из этого, предельным коэффициентом пропорциональности логично предположить 100% мощности на 1 градус. Больше не имеет смысла, так как мы хотим получить управляемость в 0.1 градуса. Минимальный, для простоты, я взял инверсным — 1% мощности на 100 градусов.
Диапазоны временных коэффициентов вычисляются просто исходя из наших условий работы регулятора. Так как мы управляем через мощностью симистор путём вычисления задержки момента включения после прохождения через 0, предельная частота работы регулятора — 50Гц. Если мы уверены, что управляем мощностью которой пофиг плюс или минус, мы можем работать на 100Гц, но это не всегда так, и потому лучше каждый раз дозировать равное количество как положительной так и отрицательной полуволны. Для упрощения жизни, я снизил время работы до 25Гц, тем самым любое вычисленное воздействие будет действовать в течение 4 полуволн, и за это время у меня будет возможность рассчитать новое воздействие.
Таким образом, постоянные времени задаются через 1/25 сек, от 0 до
2000 сек (2000*25 = 50000, как раз в 16бит влазит).
Ну и еще у нас есть ограничение мощности минимальное и максимальное, от 0 до 100%.
VI. Управление мощностью.
Начиная с этого момента все теоретические выкладки заканчиваются, начинается горькая практика, привязанная к конкретной реализации.
Итак, мы уже решили что управляем задержкой открывания симистора после прохождения через 0. Таким образом, задержка в 0 означает 100% мощность, бесконечная задержка = 0% мощности.
Вопрос: с какой точностью мы можем управлять мощностью? Вообще, с точностью отсчета времени нашего таймера. С другой стороны, какая нужна мощность? Мы вычисляем какой % мощности нужно подать на 0.04сек. В принципе, по опыту, управления мощностью даже с точностью в 1% на частоте в 0.1сек хватает для поддержания температуры в 1 градус. У нас управление 0.04сек (в 2.5раза быстрее). Поэтому было принято решение рассчитать таблицу мощности через 1/250 от максимума (с шагом в 0.4%). Это позволяет таблицу иметь не сильно большую (500 байт), и при этом иметь точность выше 1%. Если ваш случай требует бОльшей точности — пересчитать не так сложно.
Теперь поговорим о расчете этой самой таблицы. Во-1х следует учесть, что есть момент срабатывания сигнала прохождения через ноль. В моем случае — 12В. То есть когда входное напряжение упадёт ниже 12В, я получу сигнал прохождения через 0.
Это означает, что для 100% мощности время запуска = времени прохождения 12В.
Процессор у меня работает на частоте 32786, PLL настроен на 384/2, полуволна имеет 100Гц, откуда получаем, что код для загрузки константы в таймер для времени T имеет вид:
Нам нужно рассчитать время задержки, дающее равномерное увеличение площади включенной части синусоиды. То есть нам нужно иметь отсчеты времени, дающие равномерное увеличение мощности. Полная мощность, которую мы выдаём — это интеграл по всей синусоиде. [кто знает, как на хабре формулы вставлять? никак? пишу в maple-нотации тогда].
Таким образом, нам нужно пройтись по всем Q с заданной точностью, и для каждой из них найти T.
Я для себя это решил вот таким тупым способом:
Всё, на выходе мы получили табличку в 250 значений, соответствующих константам загрузки таймера до момента поджига после получения сигнала о прохождении через 0 (точнее, через 12В, как я говорил выше).
VII. Измерение входных данных
Я пропускаю этот вопрос, потому как он достоен отдельной большой статьи. О том, как я решал вопрос с термосопротивлением, можно найти в архиве почившего в бозе моего блога.
Главное что нам надо знать, это что мы измеряем данные с нужной нам частотой (в данном случае — 25Гц), и нужной точностью (на выходе — число от 0 до 2048 градусов кельвина через 1/32 градуса). Данные предполагаются уже нормализованные для всех дальнейших расчетов.
Если будет кому интересно — пишите в комментах, распишу в следующий раз как это делается для термопар.
VIII. Вычисление воздействия
И вот свершилось: у нас есть все данные для того, чтобы наконец-то произвести то, ради чего мы всё затевали: вычислить какую же мощность следует подать на управляющий элемент.
Вспомним еще раз формулу ПИД регулятора:
U = K * ( Err + (1/Ti)*Int + Td*dErr )
Мы снова пришли к вопросу, который поднимался в разделе III: этим будут пользоваться техники. Поэтомоу крайне важно не допустить классической ошибки всех реализаций — «размерности коэффициентов как получится». Мы делаем прибор для управления физическим процессом, а значит, модель должна соответствовать.
Вот теперь хорошо видно, зачем выносится за скобки пропорциональный коэффициент — это позволяет оставить диф и инт коэффициенты просто постоянными времени, в результате оператор при настройке оперирует простыми и понятными числами — процентом на градус для пропорциональной и секундами для интегральной и дифференциальной коэффициентами.
А благодаря удобному подбору положения точек и размерностей времени, как мы сейчас увидим, все расчеты производятся практически «в лоб».
Кроме одного — у нас есть величина Ti, а для расчета требуется 1/Ti. Операция деления большой разрядности — очень дорогая. Операция умножения в разы дешевле, поэтому воспользуемся отличной статьёй Division by Invariant Integers using Multiplication. У нас ведь K / Ti / Td меняются крайне редко, а потому мы можем себе позволить как угодно извращаться с ними после их изменения, главное чтобы основной цикл расчетов работал быстро.
Таким образом, вместо Ti для расчетов мы раскладываем в набор Ti_m, Ti_sh1, Ti_sh2; и на каждом цикле производим вычисление:
При всех расчетах положение точки вплоть до 7го шага остаётся на 5м справа месте. В последний момент происходит интересный финт ушами. K задаётся через 1/256, соответственно, после умножения точка сдвигается влево до 5+8=13 места, поэтому мы должны у результата отбросить младшие 8 бит. И самый нижний байт результата — нужная нам мощность через 2/5%. Это — еще одна причина, по которой мощность выровнена по шагам в 1/250 — это позволяет результат уложить в один байт и получить легко по таблице нужный результат.
Дальше, помним, что нас интересует мощность только от 0 до 250 — поэтому 7й шаг вычислений идёт очень просто, как только мы получаем отрицательное число — сразу складываем uMin. Как только выяснили что любой старший байт не ноль — сразу складываем uMax. И только если мощность складывается в диапазоне — производим проверку на меньше uMin или больше uMax.
Если вдруг кому интересно:
IX. Применение воздействия.
Итак, у нас есть рассчитанное воздействие, и наша задача — применить его. Для этого работает общий цикл работы с частотой 50Гц. На четном цикле — производится измерение и вычисление, на нечетном — применение воздействия. Таким образом, общая схема получается: выставлена мощность, через одну синусоиду производится измерение и вычисление, еще через одну — применение новой.