Вычислите чему равно отношение приращения функции y x2 4x 1 к приращению

Урок по теме: «Приращение функции»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Не всегда в жизни нас интересуют точные значения каких-либо величин. Иногда интересно узнать изменение этой величины, например, средняя скорость автобуса, отношение величины перемещения к промежутку времени и т.д. Для сравнения значения функции в некоторой точке со значениями этой же функции в других точках, удобно использовать такие понятия, как «приращение функции» и «приращение аргумента».

Понятия «приращение функции» и «приращение аргумента»

Если мы изменяем аргумент, то и значение функции тоже будет изменяться.

Приращением функции f в точке x ₀ , соответствующим приращению ∆х называется разность f(x ₀ + ∆х) – f(x ₀ ). Приращение функции обозначается следующим образом ∆f. Таким образом получаем, по определению:

Иногда, ∆f еще называют приращением зависимой переменной и для обозначения используют ∆у, если функция была, к примеру, у=f(x).

Геометрический смысл приращения

Посмотрите на следующий рисунок.

Как видите, приращение показывает изменение ординаты и абсциссы точки. А отношение приращения функции к приращению аргумента определяет угол наклона секущей, проходящей через начальное и конечное положение точки.

Рассмотрим примеры приращения функции и аргумента

Воспользуемся формулами, приведенными выше:

∆ f=f(2.1) – f(2) = 2.1 2 – 2 2 = 0.41.

Опять же, воспользуемся формулами, полученными выше.

Пример 3. . Найти приращение функции y=2x 2 при x0=3 и Δx=0,1

Решение. Подставляя в формулу, получаем, что приращение функции:

Δy=y(3+0,1)−y(3)=2 ⋅ (3+0,1) 2 −2 ⋅ 3 2 =1,22

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1547378

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Госдума приняла закон об использовании онлайн-ресурсов в школах

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Минпросвещения намерено расширить программу ускоренного обучения рабочим профессиям

Время чтения: 2 минуты

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Утверждены сроки заключительного этапа ВОШ

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Найти (с решением) производную функции.

Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.

Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.

Немного теории.

Определение производной

Определение. Пусть функция \( y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \( x_0 \). Дадим аргументу приращение \( \Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \( \Delta y \) (при переходе от точки \( x_0 \) к точке \( x_0 + \Delta x \) ) и составим отношение \( \frac<\Delta y> <\Delta x>\). Если существует предел этого отношения при \( \Delta x \rightarrow 0 \), то указанный предел называют производной функции \( y=f(x) \) в точке \( x_0 \) и обозначают \( f'(x_0) \).

Геометрический смысл производной состоит в следующем. Если к графику функции \( y = f(x) \) в точке с абсциссой \( x=a \) можно провести касательную, непараллельную оси \(y\), то \( f(a) \) выражает угловой коэффициент касательной:
\( k = f'(a) \)

Если функция \(y=f(x)\) имеет производную в точке \(x\), то ее называют дифференцируемой в точке \(x\). Процедуру нахождения производной функции \(y=f(x)\) называют дифференцированием функции \(y=f(x)\).

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция \(y=f(x)\) дифференцируема в точке \(x\). Тогда к графику функции в точке \( M(x; \; f(x)) \) можно провести касательную, причем, напомним, угловой коэффициент касательной равен \( f'(x) \). Такой график не может «разрываться» в точке \(M\), т. е. функция обязана быть непрерывной в точке \(x\).

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция \(y=f(x)\) дифференцируема в точке \(x\), то выполняется приближенное равенство \( \Delta y \approx f'(x) \cdot \Delta x \). Если в этом равенстве \( \Delta x \) устремить к нулю, то и \( \Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.

Обратное утверждение неверно. Например: функция \( y=|x|\) непрерывна везде, в частности в точке \(x=0\), но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция \( y=\sqrt[3] \) непрерывна на всей числовой прямой, в том числе в точке \(x=0\). И касательная к графику функции существует в любой точке, в том числе в точке \(x=0\). Но в этой точке касательная совпадает с осью \(y\), т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид \(x=0\). Углового коэффициента у такой прямой нет, значит, не существует и \( f'(0) \)

Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.

Правила дифференцирования

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если \(C\) — постоянное число и \( f=f(x), \; g=g(x) \) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

Источник

Эластичность функции

Содержание:

Эластичность функции

В экономических исследованиях приросты тех или иных показателей, характеризующих экономические процессы, чаще всего выражают в процентах к базовым значениям. Поэтому и изменение величин, которые связаны с ними функциональной зависимостью, также выражают в процентах. Для этого используют понятие эластичности функции, которое выражается через производную функции.

Определение и свойства эластичности функций

Пусть задана функция y = f (x). Если аргумент x получил приращение Δx и при этом функция y получила приращение Δy, то называют относительным приращением аргумента, а — относительным приращением функции.

Определение. Предел отношения относительного приращения функции к относительному приращению аргумента при условии, что приращение аргумента стремится к нулю, если существует, называется эластичностью функции.

Обозначают эластичность функции y = f (x) относительно переменной x E_x(y). То есть,

Итак, если в точке x функция имеет производную, то эластичность определяется формулой
Эластичность выражает приближенный процент приращения функции, который соответствует 1 % приращения аргумента.

Пример. Найти эластичность функции y = x 2 – 4 x +7 и вычислить ее при x = 1, x = 2, x = 5.

Решение.

Итак, если x вырастет на 1 % с 1 до 1,01, то y снизится на 0,5 %. Если x вырастет на 1 % с 2 до 2,02, то значение переменной y практически не изменится. Если x вырастет на 1 % с 5 до 5,05, то y вырастет на 2,5 %.

Свойства эластичности функции

ТЕОРЕМА 1. Эластичность произведения двух функций равна сумме эластичности сомножителей:
E_x (U ⋅ V) = E_x (U) + E_x (V).

Доказательство. По определению эластичности

ТЕОРЕМА 2. Эластичность частного двух функций равна разности показателей эластичности делимого и делителя:

Доказательство. По определению эластичности

Эластичность спроса относительно цены

В анализе и прогнозах ценовой политики применяется понятие эластичности спроса и предложения.

Пусть p цена одного изделия, а Q — количество изделий, произведенных и проданных через некоторое время, что определяет спрос. Величина Q зависит от цены, т. е. Q является функцией от p: Q = f (p).

Пусть приращение цены Δp вызывает приращение ΔQ. тогда относительные приращения цены и спроса будут соответственно и
Отношение показывает относительное изменение спроса, если цена изделия возросла на 1 %.

Эластичностью спроса относительно цены называется предел отношения относительного приращения спроса к относительному приращению цены при условии, что приращение цены стремится к нулю.

Эластичность спроса относительно цены приближенно определяет, как меняется спрос на данное изделие, если его цена возрастает на 1 %.

Так, например, если рост цены на 5 % вызывает падение спроса на 8 %, то эластичность будет
Если эластичность спроса η = –0,5, то 10 % роста стоимости товара вызывает падение спроса на (–0,5) 10% = –5%.

Эластичность предложения относительно цены

Понятие эластичности можно применять и к другим функциям экономического содержания.

Рассмотрим понятие эластичности предложения S в зависимости от цены товара p. Под предложением понимают количество некоторого товара, который предлагается на продажу за единицу времени. Как правило, предложение какого-либо товара является возрастающей функцией цены. Но бывают случаи, когда предложение повышается со снижением цены. Величина S является функцией от цены товара. То есть, S = S (p).

Пусть Δp — приращение цены, а ΔS — соответствующее приращение предложения. Тогда относительные приращения цены и предложения будут соответственно и .
Эластичностью предложения относительно цены называется предел отношения относительного приращения предложения к относительному приращению цены при условии, что приращение цены стремится к нулю.

Эластичность предложения относительно цены приближенно определяет процент приращения предложения на 1 % приращения цены.

Пример 3. Функция предложения некоторого товара . Определить эластичность предложения при цене p = 2.

Решение.

Если p = 2, то
Следовательно, при цене p = 2 увеличение ее на 1 % вызовет увеличение предложения на 0,2 %.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Вычислите чему равно отношение приращения функции y x2 4x 1 к приращению

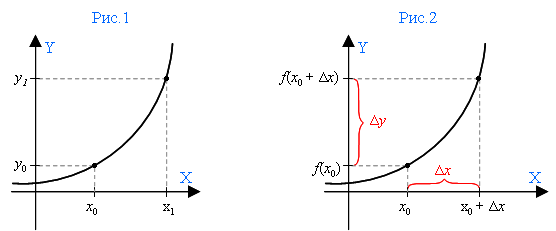
Приращение аргумента и функции

На оси Х – две точки: x₀ и x₁ (рис.1). Если от x₁ отнимем x₀, то узнаем длину шага между ними – а говоря иначе, узнаем, на сколько приросла точка x₀ в точке x₁. Эта разность между двумя заданными точками оси X и называется приращением аргумента.

Точки x₀ и x₁ образуют на оси Y соответственно точки у₀ и у₁. Если от у₁ отнять у₀, то мы получим приращение функции.

Итак, в функции y = f(x) относительно определенных точек x₀ и x₁:
разность x₁ – x₀ называется приращением аргумента, а разность у₁ – у₀ называется приращением функции.

Приращение обозначается греческой буквой Δ (дельта):

Можно сказать и иначе: если к x₀ прибавить величину приращения Δx, то мы получим точку x₁.
То есть x₁ = x₀ + Δx (рис.2).
Тогда точку f(x₁), отмеченную на первом рисунке как у₁, тоже можно обозначить иначе:
f(x₀ + Δx).

Осталось вывести формулу приращения функции.

Формула приращения функции:

Δy = f(x₀ + Δx) – f(x₀)

Δf = f(x₀ + Δx) – f(x₀)

Источник