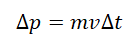Выражение ноль на массу что значит
Закон cохранения импульса
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела
→ →
p = mv
p — импульс тела [кг*м/с]
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
Векторная сумма импульсов тел в замкнутой системе постоянна
А выглядит — вот так:
Закон сохранения импульса
→ → →
p1 + p2 + … + pn = const
p — импульс тела [кг*м/с]
Простая задачка
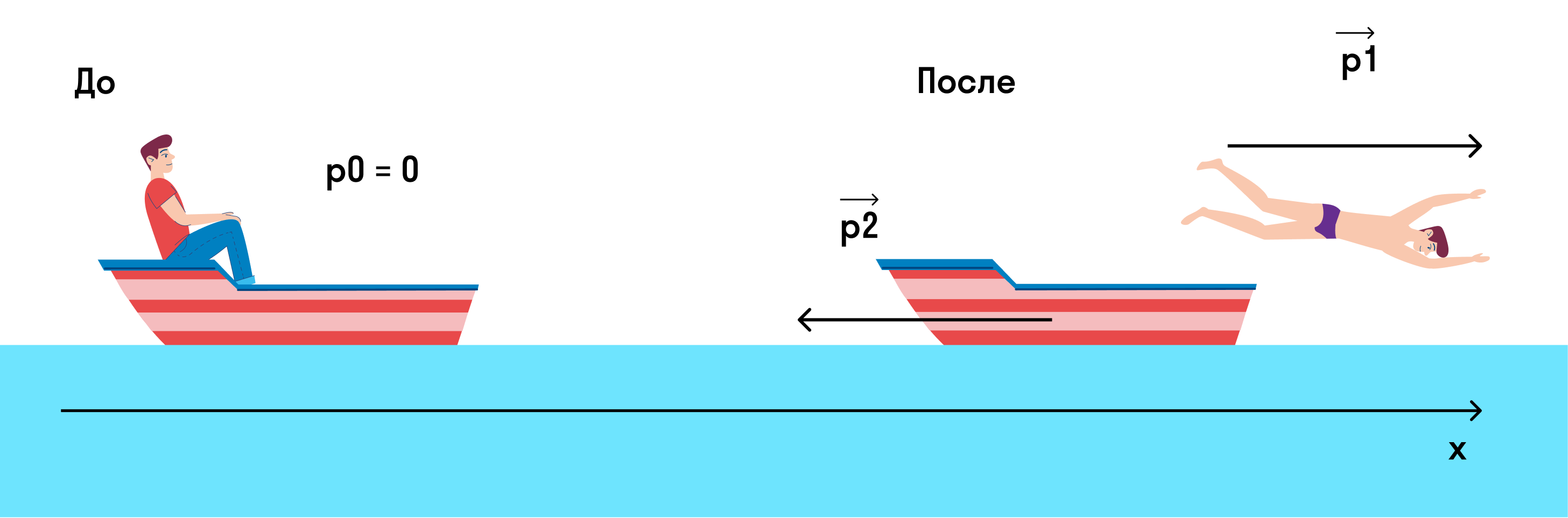
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
p0 — это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
p1 — это импульс мальчика после прыжка,
p2 — это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
0 = p1 — p2
p1 = p2
Подставим формулу импульса.
mV1 = MV2
Выразим скорость лодки V2:
V2 = mV1/M
Подставим значения:
V2 = 45*3/270 = 3/6 = ½ = 0,5 м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
Задачка посложнее
Решение: Для данной системы выполняется закон сохранения импульса:
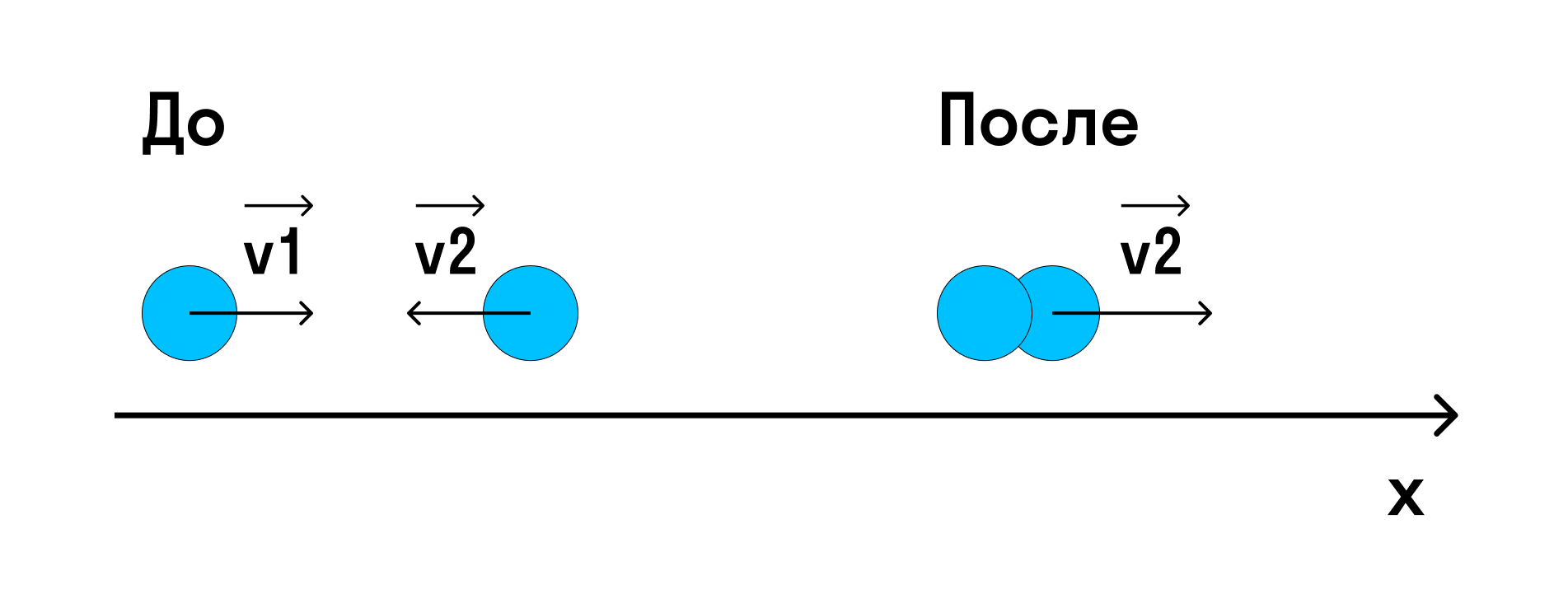
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы m1 + m2, которое движется с искомой скоростью:
m1v1 — mv2 = (m1 + m2) v
Отсюда находим скорость тела, образовавшегося после удара:
v = (m1v1 — mv2)/(m1 + m2)
Переводим массу в килограммы и подставляем значения:
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на значение получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится Δv =v —v0 — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
То есть, вектор Δv⋅m – это вектор Δp.
Тогда второй закон Ньютона в импульсной форме запишем так
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме
Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила F2 называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
mг vг = mр vр,
где mг — это масса горючего,
vг — скорость горючего,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
Скорость ракеты при реактивном движении
vр = mг vг / mр
mг — это масса горючего [кг]
vг — скорость горючего [м/с]
mр — масса ракеты [кг]
v р — скорость ракеты [м/с]
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Пропала «масса» на автомобиле: что это значит, и как это устранить?
«Пропала «масса!» – именно это заклинание мы чаще всего слышим при обращении к автоэлектрикам с какими-либо неисправностями в электрооборудовании машины. Что полезно знать о «массе» в автомобиле, и как своими руками поправить дело при ее исчезновении?
Два провода или один?
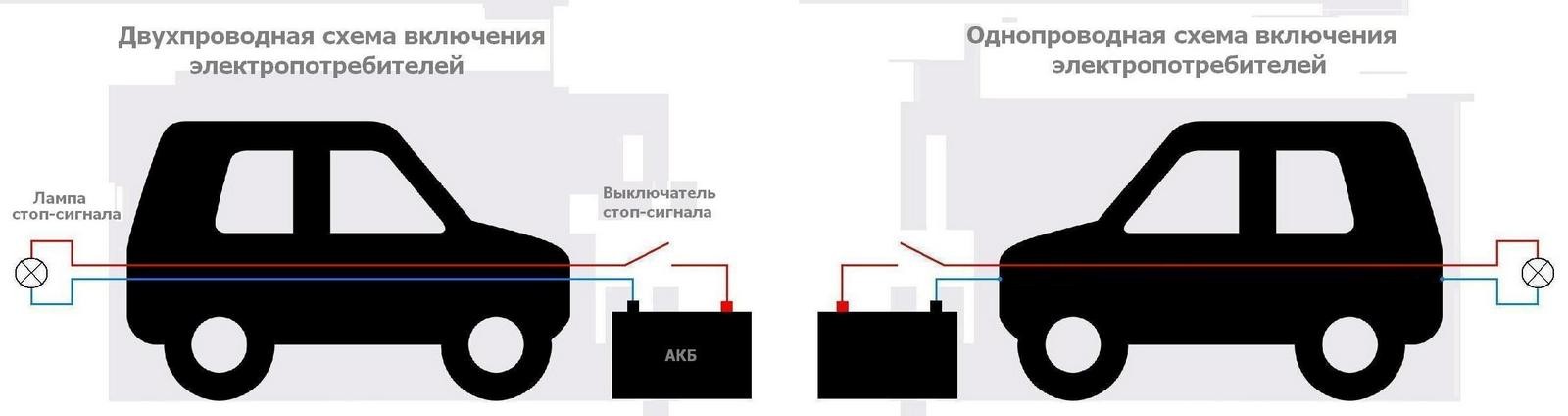
Д ля подключения полезной нагрузки к источнику электропитания требуются два провода – об этом знает даже школьник (хотя Никола Тесла считал иначе…). Самый очевидный пример, вполне возможно, находящийся сейчас прямо рядом с вами – настольная лампа, включенная в розетку. Примерно так же включались и немногочисленные потребители электроэнергии на первых автомобилях конца XIX – начала XX веков. Схема простая, надежная и вполне жизнеспособная.
Однако как только выпуск автомобилей стал хоть сколько-либо массовым, коммерческая мысль промышленников тут же пошла в направлении экономии и оптимизации, и количество проводов в машине разом сократилось вдвое – в качестве одного из проводов стала использоваться металлическая масса кузова – в просторечии та самая «масса».
На донельзя упрощенной, но вполне наглядной вышеприведенной картинке справа изображена современная схема электрооборудования автомобилей – когда «массой» является минусовой провод бортовой сети. Однако так было не всегда… Приблизительно до 50-х годов ХХ века автопроизводители использовали в качестве «массы» как минус, так и плюс.
Стандарты в автопроме тогда еще не устоялись, а с электротехнической точки зрения не было совершенно никакой разницы, пускать по кузову плюс или минус. Однако к середине века наблюдения выявили более заметное коррозионное разрушение кузовов тех автомобилей, в которых «массой» был именно плюс! Выяснилось, что в этом случае интенсивнее развивается электрохимическая коррозия, обусловленная направлением движения электронов в электрической цепи — от плюса к минусу. В итоге от плюсовой «массы» повсеместно отказались в пользу минусовой – тем более что это не требовало ни малейших дополнительных вложений в производство.
Замена плюса на минус
Среди моделей отечественного автопрома плюс на «массе» встречался у Победы, у Москвичей 401-402 и более ранних, у первого выпуска «21-й» Волги (с 1960 года систему электрооборудования ГАЗ-21 поменяли на традиционную для наших дней). Автомобиль в СССР был товаром сверхдлительного использования, передаваясь из поколения в поколение десятилетиями, и после того как стало известно о вредоносном влиянии плюсовой «массы», изрядное количество владельцев старых Москвичей, Побед и Волг взялось самостоятельно переделывать полярность в электросистеме своих авто. Тем более что в литературе для автомобилистов того времени было немало советов и рекомендаций по такому апгрейду.
В принципе, рукастый автолюбитель справлялся с работой по переделке за один день. Помимо банальной смены клемм на аккумуляторе требовалось поменять полярность у амперметра указателя зарядки на приборной панели и немножко поковыряться с паяльником в радиоприемниках моделей А-8, А-9 и А-12, с плюсом на корпусе. Самым сложным была переполюсовка генератора, а вот моторчики печки и дворников и стартер, в которых не было постоянных магнитов, работали при изменении полярности точно так же и в доработках не нуждались.
На фото: ГАЗ-М21 Волга (I) ‘1956–1958
Сегодня же, как ни странно, наблюдается обратная эволюция! Владельцы редких и восстановленных ГАЗ-21 первой серии и Побед в борьбе за полную аутентичность возвращают автомобилям изначальную конфигурацию электрооборудования, измененную когда-то прежними хозяевами. Усиливающаяся коррозия их уже не беспокоит, поскольку такие машины обычно не используются «на повседневку», 99% времени стоят с отключенной батареей и выезжают лишь несколько раз в год на автофестивали и ретропробеги.
«Аналог» и «цифра» – «масса» нужна всем!
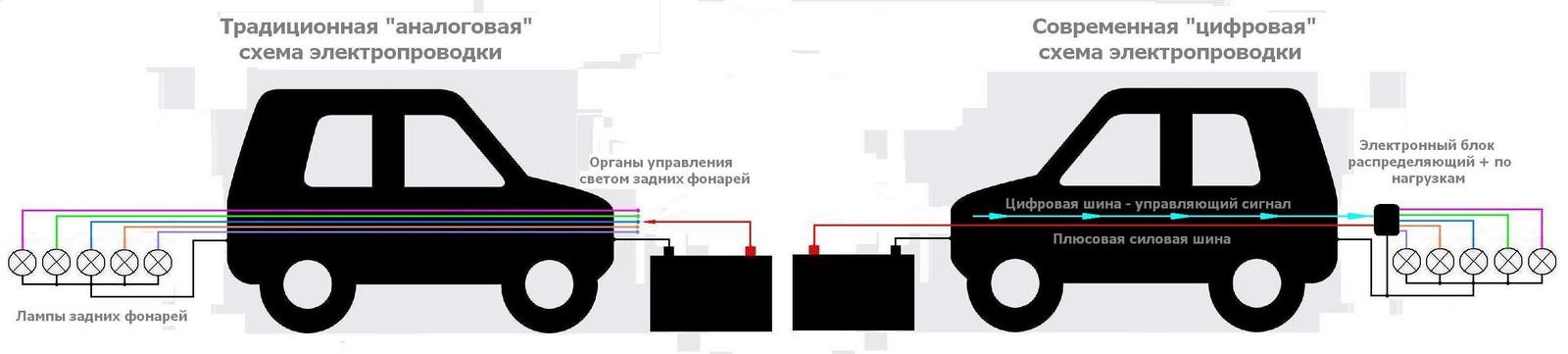
Сегодня во многих авто применяется управление электрикой и электроникой по цифровой шине данных. Это дает огромную гибкость в управлении многочисленной электроникой, а также экономию меди – последнее, к слову, вторично.
На простейшем примере это выглядит так. В традиционной электросхеме к многочисленным лампочкам задних фонарей идет через весь кузов как минимум 5 плюсовых проводов — стоп-сигнал, два поворотника, габариты и задний ход (минусовым, разумеется, является кузовная «масса»). В цифровой же конфигурации плюсовой провод – всего один, и еще один тонкий – цифровая шина. По ней блок управления, расположенный непосредственно возле задних фонарей, получает команды и раздает «плюс» тем лампам, которым он в данный момент требуется.
Однако, несмотря на такое изменение концепции электрооборудования, роль «массы», разумеется, не исчезает – наоборот, она даже заметно возрастает! Ибо цифровые блоки управления гораздо чувствительнее к ухудшению контакта с «массой», нежели грубые и «неумные» лампочки и моторчики исполнительных устройств, которые раньше получали питание по простым «аналоговым» плюсовым проводам.
В поисках «массы»
«Пропала масса!» — едва ли не самая любимая мантра автомобильных электриков, поминаемая ими и по делу, и всуе… Слыша это многократно, многие автовладельцы, помнящие как минимум электротехнику по школьной физике, задумываются – кстати, а почему почти всегда теряется именно минусовая «масса», а не плюс? Ведь, казалось бы, они равнозначно необходимы для подвода тока к потребителю…
Ответ тут прост. В силу того, что общий массовый провод, коим является кузов, открыт атмосферной влаге и склонен к коррозии, элементы и модули электрики электроники автомобиля часто лишаются именно минуса или получают его через повышенное сопротивление ржавого и окислившегося контакта. Контакт в плюсовых проводах тоже порой теряется, но, поскольку в них почти не используется склонная к ржавлению сталь, происходит потеря контакта в разы реже, чем в случае с минусом…
В принципе, процедура поиска и восстановления плохого контакта в точках подключения к «массе» несложна и доступна большинству автовладельцев, практикующих самостоятельное обслуживание личного авто. Большинство контактных точек под капотом нетрудно обнаружить вдумчивым разглядыванием. В салоне и багажнике несколько сложнее – немало точек «массы» прячутся под торпедо и обшивками. Но и они конечном счете обнаружимы.
Обычно точки подключения электропроводки к «массе» представляют собой резьбовые шпильки, приваренные к кузову, или резьбовые закладные гайки. Так или иначе, ржавая и окисленная точка «массы» должна быть развинчена гаечным ключом, наконечники проводов, площадка вокруг шпильки, шайбы и гайка зачищены наждачкой, для предупреждения попадания влаги смазаны специальной аэрозольной смазкой для электроконтактов (или, в крайнем случае, консистентными смазками типа Литол-24 или графитки) и собраны в обратном порядке.
Особенно стоит отметить важность так называемых «корончатых» шайб, которые по науке именуются «шайбы стопорные с наружными зубьями» (они же иногда бывают интегрированы в кабельные наконечники). Эта мелкая и, на первый взгляд, не заслуживающая внимания ерундовина крайне важна для обеспечения качественного контакта в точках «массы»!
Дело в том, что кузов на заводе красится в полностью собранном виде – после окраски на нем уже ничего не сверлят и не варят. Соответственно, все резьбовые шпильки, являющиеся точками контакта с «массой», а также места вокруг них оказываются покрытыми краской, которая не проводит электрический ток. Поэтому под кабельный наконечник, надеваемый на шпильку, подкладывается специальная зубчатая шайба – она точечно нарушает изоляцию краски и обеспечивает суммарную большую площадь контакта без риска разрастания ржавого пятна вокруг шпильки со временем. Отсутствие таких шайб – недопустимо, замена их на обычные плоские или гроверные – тоже. Плюс нужно знать, что они, по-хорошему, одноразовые. Однако часто после кузовного ремонта сборщики эти шайбы забывают или игнорируют.
Бывают и курьезные случаи – к примеру, на продукции АвтоВАЗа лет несколько назад владельцы отмечали массовую (вот уж каламбур) проблему плохого контакта в точках массы из-за применения на заводском конвейере странных корончатых шайб, покрытых плохо проводящим ток черным анодированием.
К слову, применять эти шайбы бездумно и лепить их повсюду не стоит! К примеру, плюсовой контакт стартера в них совершенно не нуждается – там гораздо полезнее будут две обычные плоские шайбы и гровер.
Забавно, но порой в поисках «массы» доходят до изрядных крайностей. Отдельная история – так называемая «разминусовка». Сия процедура представляет собой ручное изготовление целого вороха толстенных проводов с клеммами под болт на концах и соединение ими с «массой» и непосредственно с минусовой клеммой аккумулятора под капотом всего того, что уже и так с ними соединено – двигателя, стартера, КПП и прочего.
На самом деле процедура это совершенно безобидная, невредная и даже порой полезная. Изначально она использовалась как метод ремонта и профилактики электрики в немолодых авто, где сложно диагностировать проблемы с «массой». Поэтому вместо замены всей проводки целиком просто пробрасывали качественную дублирующую «массу» везде, где только можно. В результате удавалось устранять трудные «плавающие» проблемы и глюки электрооборудования малой кровью.
Однако впоследствии «разминусовка» превратилась из метода упрощенного ремонта в странноватое «полутюнинговое» мероприятие… Немыслимой толщины провода упаковываются в красивую декоративную изоляцию «а-ля змеиная кожа» и используются фактически для украшения подкапотного пространства. Хотя и с изначальным посылом улучшения стабильности работы двигателя и прочей электроники.
Импульс тела, закон сохранения импульса
теория по физике 🧲 законы сохранения
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p 1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
Изменение импульса тела
∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар
Конечный импульс тела:
Модуль изменения импульса тела равен модулю его начального импульса:
Абсолютно упругий удар
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Пуля пробила стенку
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:
Радиус-вектор тела повернул на 180 градусов
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Угол падения равен углу отражения:
Модуль изменения импульса в этом случае определяется формулой:
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:
Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено