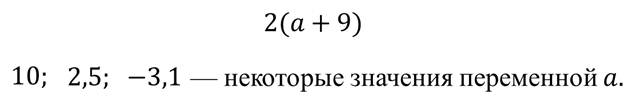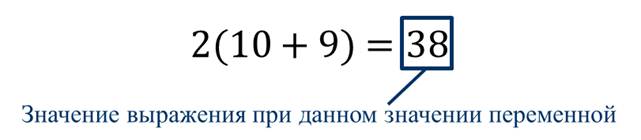Выражение с переменными что это такое

Числовые, буквенные выражения и выражения с переменными: определения, примеры.

Запись условий задач с помощью принятых в математике обозначений приводит к появлению так называемых математических выражений, которые называют просто выражениями. В этой статье мы подробно поговорим про числовые, буквенные выражения и выражения с переменными: дадим определения и приведем примеры выражений каждого вида.

Навигация по странице.

Числовые выражения – что это?

Можно сделать вывод, что на этом этапе изучения математики числовыми выражениями называют имеющие математический смысл записи, составленные из чисел, скобок и знаков сложения и вычитания.

А в старших классах разнообразие записей числовых выражений разрастается как снежный ком, катящийся с горы. В них появляются обыкновенные и десятичные дроби, смешанные числа и отрицательные числа, степени, корни, логарифмы, синусы, косинусы и так далее.

Обобщим всю информацию в определение числового выражения:

Разъясним все составные части озвученного определения.

В числовых выражениях могут участвовать абсолютно любые числа: от натуральных до действительных, и даже комплексных. То есть, в числовых выражениях можно встретить

Что касается скобок, то имеют место как числовые выражения, в которых есть скобки, так и выражения без них. Если в числовом выражении есть скобки, то они в основном

В качестве специальных математических символов и обозначений, которые можно встретить в числовых выражениях, приведем знак модуля. Для примера покажем числовое выражение с модулем .

Что такое буквенные выражения?

Итак, если допустить в числовом выражении присутствие букв, которыми обозначены некоторые числа, то получится так называемое буквенное выражение. Дадим соответствующее определение.

Выражение, содержащее буквы, которыми обозначены некоторые числа, называется буквенным выражением.

Из данного определения понятно, что принципиально буквенное выражение отличается от числового выражения тем, что может содержать буквы. Обычно в буквенных выражениях используются маленькие буквы латинского алфавита ( a, b, c, … ), а при обозначении углов – маленькие буквы греческого алфавита ( α, β, γ, … ).

Итак, буквенные выражения могут быть составлены из чисел, букв и содержать все математические символы, которые могут встречаться в числовых выражениях, такие как скобки, знаки корней, логарифмы, тригонометрические и другие функции и т.п. Отдельно подчеркнем, что буквенное выражение содержит по крайней мере одну букву. Но может содержать и несколько одинаковых или различных букв.

Выражения с переменными

Если в буквенном выражении буква обозначает величину, которая принимает не какое-то одно конкретное значение, а может принимать различные значения, то эту букву называют переменной и выражение называют выражением с переменной.

Выражение с переменными – это буквенное выражение, в котором буквы (все или некоторые) обозначают величины, принимающие различные значения.

Вообще, переход от понятия буквенного выражения к выражению с переменными происходит в 7 классе, когда начинают изучать алгебру. До этого момента буквенные выражения моделировали какие-то конкретные задачи. В алгебре же начинают смотреть на выражение более общо, без привязки к конкретной задаче, с пониманием того, что данное выражение подходит под огромное число задач.

В заключение этого пункта обратим внимание еще на один момент: по внешнему виду буквенного выражения невозможно узнать, являются ли входящие в него буквы переменными или нет. Поэтому ничто нам не мешает считать эти буквы переменными. При этом разница между терминами «буквенное выражение» и «выражение с переменными» исчезает.

Источник

Выражения с переменными

Урок 2. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Выражения с переменными»

· ввести понятие «выражение с переменными»;

· ввести понятие «область определения выражения».

Вспомним, что на прошлом уроке мы говорили о числовых выражениях и значениях числовых выражений.

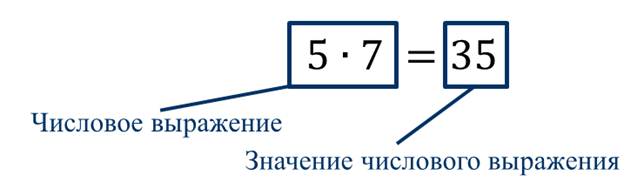
Числовым выражением называется запись, составленная из чисел, знаков арифметических действий и скобок, указывающих на порядок выполнения действий.

Значением числового выражения называется число, которое получается при выполнении всех действий числового выражения.

Буквенным выражением называется запись, состоящая из чисел, букв, знаков арифметических действий и скобок, указывающих на порядок выполнения действий.

Строчные буквы латинского алфавита чаще всего используют при записи буквенных выражений.

Следует также знать, что и одна буква является буквенным выражением.

Давайте решим задачу.

Велосипедист двигается со скорость 15 километров в час. Какой путь он проедет за время t?

Известно, что путь можно найти скорость умножив на время. Тогда путь, который проедет велосипедист, будет равен 15t.

Теперь, если нам нужно будет узнать, какое расстояние проехал велосипедист, например, за 3 часа, мы подставим в выражение 15 ∙ t вместо буквы t число 3, то есть найдём значение выражения при t = 3, и получим 45 километров.

В нашем случае буква t называется переменой, а само выражение – выражением с переменной.

То есть, переменная – это буква, входящая в буквенное выражение, которая может принимать различные значения.

Если мы в выражение с переменной вместо переменной подставим число, то получим числовое выражение.

Теперь, прежде, чем перейти к решению упражнений, вернёмся к выражению 15t, которое мы получили при решении первой задачи. Здесь переменная t может принимать только положительные значения, так как время не может быть отрицательным, и это множество значений называется областью определения выражения 15t.

Таким образом, важно помнить, что в область определения любого выражения могут входить только те значения переменных, при которых получается числовое равенство, имеющее смысл.

А сейчас давайте решим некоторые упражнения.

Источник

Числовые выражения. Выражения с переменными. Примеры упрощения выражений

Числовое выражение – это совокупность одного или нескольких чисел и функций, соединенных знаками арифметических операций и скобками.

Примеры числовых выражений:

Значением числового выражения является число.

Операции в числовом выражении выполняются в следующей последовательности:

1. Действия в скобках.

2. Вычисление функций.

3. Возведение в степень

4. Умножение и деление.

5. Сложение и вычитание.

6. Однотипные операции выполняются слева на право.

Так значением первого выражения будет само число 12,3

Для того чтобы вычислить значение второго выражения, действия будем выполнять в следующей последовательности:

3. Выполним последовательно операции слева направо:

Выражение с переменными – это совокупность одного или нескольких чисел, переменных и функций, соединенных знаками арифметических операций и скобками. Значения выражений с переменными зависят от значений, входящих в него переменных. Последовательность выполнения операций здесь та же, что и для числовых выражений. Выражения с переменными иногда бывает полезно упрощать, выполняя различные действия – вынесение за скобки, раскрытие скобок, группировки, сокращение дробей, приведение подобных и т.д. Так же для упрощения выражений часто используют различные формулы, например, формулы сокращенного умножения, свойства различных функций и т. д.

Пример: Упростить выражение 3 • (x – 4 • y + 11) + 12 • y – 30

3 • (x – 4 • y + 11) + 12 • y – 30 = 3 • x – 12 • y + 33 + 12 • y – 30;

2. Приведем подобные:

3. Теперь можно оставить выражение в таком виде, а можно вынести 3 за скобки:

Ошибка в тексте? Выдели её мышкой и нажми

Источник

Значения числовых и буквенных выражений. Выражения с переменными

Значения числовых и буквенных выражений. Выражения с переменными

В статье рассмотрены наиболее популярные темы, которые встречаются в контрольно – измерительных материалах по математике. Все задания составляются в соответствии с кодификатором требований о подготовке к ЕГЭ.

В задания ЕГЭ по математике базового уровня входят следующие темы о значении:

— Выражений с переменными;

Раздел Преобразование буквенных выражений содержит в себе небольшие подразделы, которые включают темы о преобразовании выражений, включающих:

Данные задания ЕГЭ по математике 2020 встречаются довольно часто, поэтому перед тем как приступить к разбору вышеописанных тем, нужно изучить само понятие о значении выражения.

Рассмотрим определение данного понятия. Значение выражения – это цифра, которая получается после выполнения необходимых операций с выражением.

Данное определение также называют числом с набором следующих действий: сложение, вычитание, деление и умножение.

Рассмотрим пример: 1+2. Данное выражение представляет собой сложение чисел, ответом будет число 3 – это значение выражения.

Обычно при нахождении значения у числового выражения, слово «числового» не используют, так как в данном случае понятно, что имеется в виду. Существуют числовые выражения, у которых невозможно найти значение, так как необходимо выполнить действия, не имеющие смысла, например, разделить на нуль. В таких случаях считают, что у выражения нет решения.

Такими выражениями принято называть выражения с наличием букв. Если заменить буквы на число, то получится выражение, содержащее числа.

Рассмотрим пример: 2 * х + у, пусть х = 1, у = 2. Далее следует заменить буквы цифрами, и высчитать значение выражения: 2 * 1 + 2= 4. Ответ: 4.

В математике буквы в выражении принимают разные значения, при этом буквы — переменные, а выражения с наличием букв – выражения, содержащие переменные.

Выражения, содержащие переменные

Значением таких выражений называют значения числовых выражений, которые получены путём подстановки. Пример: 3 * а * в + в, пусть а = 2, в = 1. Теперь поставляем числа в само выражение и получаем: 3 * 2 * 1 + 1 = 7. Ответ: 7. В некоторых случаях переменные могут быть разные, но значение выражений у этих переменных должно быть единое.

Значение у переменной можно задавать из допустимого значения, соответствующего им. Так как в другом варианте, при подстановке значений, которые не принадлежат области с допустимыми значениями, получится выражение, не имеющее смысла.

Также нужно учитывать, что бывают выражения с переменными, у которых значение не имеет подчинённости от заданных переменных. Например: 5 + х – х. В данном случае значение выражения не связано с переменной х. Во всех случая значение выражения будет равняться пяти.

Преобразование буквенных выражений может быть включать:

Рассмотрим каждый вид преобразования по отдельности.

Преобразование буквенных выражений, имеющих степени

Рассмотрим несколько правил преобразования степенных выражений:

— Произведение с одинаковыми основаниями ( а^p * a^q = a^ (p+ q ); a^ ( p + q) = а^p * a^q );

— Частное с равными показателями (а^p / a^q = a^(p – q ); a^(p – q ) = а^p / a^q = ф^p / a^ q );

— Степень в степени ( a^p )^q = a^pq; a^pq = ( a^p )^q = ( a^q )^p);

— Степени произведения с частным ( ab^p = a^p * b^p; (a / b)^p = ( a^p ) / (b^p); a^p * b^p = ab^p; ( a^p ) / (b^p = (a / b)^p.

Рассмотрим примеры таких преобразований.

Преобразование буквенных выражений с радикалами

Данная тема содержится в КИМах ЕГЭ по математике, она изучается 7 классе по алгебре, приступим к рассмотрению. Радикалом называют подкоренное выражение. Рассмотрим необходимые формулы, которые будут полезны в процессе преобразования:

Данные выражения принимают за иррациональные. Для наглядности разберём пример иррационального преобразования:

Нужно упростить данное выражение: 4 √32^5.

Данное выражение нужно представить в виде: 16 – a^4 – 2a и воспользоваться второй формулой: 4 √32^5 = 4 √16 * 4 √a^4 * 4 √2a = 2a 4√2a.

Преобразование выражений, содержащих логарифмы

В некоторых КИМах могут встречаться задания на преобразование выражений с логарифмами.

Данные преобразования производятся в соответствии со свойствами логарифмов. Для решения подобных заданий следует знать свойства логарифмов, которые могут решить задачу.

— loga b^m = m log a b;

— loga^k b^m = m/k loga b;

— loga b = logc b/logc a;

— loga b * logc d = logc d * loga d;

— a logc b = b logc a.

Вышеизложенные свойства можно применять в любом порядке. При подготовке к ЕГЭ по математике нужно тщательно повторить данные свойства, также важно уметь их использовать в процессе преобразования выражений. Начать следует с числовых выражений. Но как же найти свойство, с помощью которого преобразовать выражение? Обычно это несложно, следует сопоставить логарифм, который нужно преобразовать и выражение, содержащее свойства логарифмов.

Преобразование выражений, содержащих функции тригонометрии

Под данным термином понимают упрощение выражений, используя формулы из тригонометрии.

Существуют правила, которым нужно следовать в процессе преобразования выражений:

— Если выражение имеет больше количество тригонометрических функций, следует сократить их количество, здесь нужно применять тождества тригонометрии;

— Выражение, содержащее разные аргументы следует привести к единому;

— Для того чтобы получить функцию, следует воспользоваться формулами;

— Если в выражении присутствуют функции высоких степеней, следует воспользоваться тождествами тригонометрии или применить формулы, с помощью которых можно понизить степень.

— tg a = sin a / cos a, ctg a = cos a / sin a;

Рассмотрим пример. Нужно упростить выражение: cos^2 a / 2 – 1 / 2 cos a. Применяем формулу, с помощью которой можно понизить степень: ( cos a + 1 ) / 2 – 1 / 2 cos a = 1 / 2.

После изучения данной темы и рассмотрения примеров рекомендуем прочитать литературу с более подробным разбором примеров ЕГЭ по математике, изучив данные, а также дополнительные материалы вы в совершенстве будете владеть темой значения числовых и буквенных выражений.

Источник

Как вы решаете выражения с переменными?

В связи с этим, как решить выражение с одной переменной?

Что касается этого, что такое пример выражения?

Кроме того, как вы вычисляете выражения?

Чтобы вычислить алгебраическое выражение, вы должны подставьте число для каждой переменной и выполните арифметические операции. В приведенном выше примере переменная x равна 6, поскольку 6 + 6 = 12. Если мы знаем значения наших переменных, мы можем заменить переменные их значениями, а затем оценить выражение.

Как упростить примеры алгебраических выражений?
Упрощение выражений

Что такое выражение в одной переменной?

Как объяснить выражения?

Изучающие английский язык Определение выражения

Что такое слова выражения?

имя существительное. акт выражения или изложения словами: свободное выражение политических взглядов. определенное слово, фраза или форма слов: старомодные выражения. способ или форма, в которой вещь выражена словами; формулировка; формулировка: деликатность выражения.

Как определить алгебраическое выражение?

Как найти эквивалентные выражения?

Комбинируйте любые одинаковые члены с каждой стороны уравнения: x-члены с x-членами и константы с константами. Расположите члены в том же порядке, обычно x-член перед константами. Если все термины в двух выражениях идентичны, то два выражения эквивалентны.

Каков пример упрощения?

Что такое примеры алгебраических выражений?

Алгебраические выражения включают как минимум одну переменную и как минимум одну операцию (сложение, вычитание, умножение, деление). Например, 2 (х + 8у) является алгебраическим выражением.

Как вы вычисляете выражения?

Чтобы оценить выражение, мы замените данное число на переменную в выражении а затем упростите выражение, используя порядок операций. Чтобы оценить, замените x в выражении 3, а затем упростите.

Как вы описываете нервное выражение лица?

Однако в целом, чтобы описать выражение страха, вы должны следовать следующим рекомендациям: Их брови будут подняты и вместе. Их верхние веки будут подняты, и их нижние веки тоже будут напряжены и приподняты. Их рот будет вытянут и отведен назад, возможно, обнажив зубы.

Как описать выражение в математике?

Что такое выражение и уравнение?

Выражение число, переменная, или комбинация чисел, переменных и символов операций. Уравнение состоит из двух выражений, соединенных знаком равенства.

Какие бывают два типа выражений?

An арифметическое выражение оценивается в одно арифметическое значение. Символьное выражение оценивается как одно значение типа character. Логическое или реляционное выражение дает одно логическое значение.

Что такое выражение и предложение?

Что такое обычное выражение?

Это слова или фразы, которые не следует понимать буквально. Например, если вы говорите, что у кого-то «холодные ноги», это не значит, что у него на самом деле холодные пальцы ног. Скорее, это означает, что они чем-то нервничают. … Если понимать буквально, можно подумать, что у кого-то холодные ноги мерзнут.

Какие 3 части выражения?

Какими двумя способами можно написать эквивалентные алгебраические выражения?

Другие ответы 3 (x + 3) и 3x + 9 являются эквивалентными выражениями, потому что значения обоих выражений остаются одинаковыми для любого значения x. Выражения 6 (x 2 + y + 2) и 6 × 2 + 6y + 12 являются эквивалентными выражениями и также могут быть записаны как 6 (x2 + y + 2) = 6 × 2 + 6y + 12.

Какой пример эквивалентного выражения?

Примеры эквивалентных выражений

3 (x + 2) и 3x + 6 являются эквивалентными выражениями, потому что значения обоих выражений остаются одинаковыми для любого значения x. 3x + 6 = 3 × 4 + 6 = 18. и также может быть записано как 6 (x 2 + 2у + 1) = 6х 2 + 12y + 6. В этом уроке мы учимся определять эквивалентные выражения.

Как упростить тригонометрические выражения?

Какое правило из шести букв упрощает выражения?

Ответ: Удалите любой символ группировки, такой как скобки и круглые скобки, путем умножения множителей..

Источник