Выражение средняя температура по больнице что означает
Выражение средняя температура по больнице что означает
Виктор тогда шо если одна соседка б—ь, вторая, шов среднем и моя жена тоже.
Если усреднения доводить до абсурда, то можно и так считать.
Выражение современного русского языка, означающее некорректную статистику, когда для создания благополучной картины манипулируют статистическими данными и сравнивают несравниваемые показатели.
полноценный ответ.Спасибо.Наконец поняла что к чему.
Это выражение, насколько я знаю, придумано преподавателями экономико-статистического института в 1960-е годы. Как иллюстрация того, что статистика применима не везде.
она всегда была ложью.Но нужна она,ложь,нам.Почему мы должны жить по законам это лжи,которую придуываем мы сами?
)))) Статистика как наука очень полезна. Например, вся теория измерений строится на статистике. Просто неумелое (часто осознанно неумелое) ее применение несет большие беды.
«Средняя температура по больнице» – почему эта аналогия обычно хромает?
Аналогия полезна для понимания сущности вещей, скрытых за статистикой, когда используется по назначению. Но ею часто злоупотребляют, из-за чего она легко превращается в демагогический прием.
Несколько соображений по этому поводу.
Начнем со сферы ее полезного применения. Здесь проще всего отталкиваться от самого этого медицинского показателя. У него имеется всем известное значение, используемое как критерий здорового состояния, – 36.6. Отклонение от него в обе стороны говорит о проблемах со здоровьем. Этим объясняется нецелесообразность использования глобальных средних для этого показателя. Ведь больные могут быть с температурой и выше, и ниже нормы, и усреднение их температур легко может дать близкое к норме значение, введя в заблуждение о среднем состоянии здоровья пациентов больницы.
Даже если среднее отличается от уровня здоровья, оно все равно будет вводить в заблуждение, давая заниженную оценку температуры тех, у кого она высокая, за счет низких значений у больных с температурой ниже нормы. То же самое верно и в отношении последних, только наоборот.
Однако это не означает, что среднее вообще не годится как описательная статистика для температуры тела. Его вполне можно использовать, чтобы составить общее представление о состоянии тех больных, недуг которых порождает отклонение температуры от нормы в одну и ту же сторону. Напр., можно выделить в отдельную группу больных ГРИППом с повышенной температурой. Среднее для этой группы уже сгодится как статистика, дающая общую картину протекания болезни. Такое среднее можно будет сравнивать между больницами или между сезонами. Разница в средней температуре всех больных в двух больницах ни о чем не говорит, а та же разница в отношении лишь страдающих конкретной болезнью позволяет увидеть, в которой из больниц пациентам этой категории хуже.
Теперь можно перейти к экономическим показателям в том же контексте. Самый распространенный показатель экономического здоровья – уровень доходов. Его ключевое отличие от температуры тела в том, что здесь «много не бывает». Хотя к доходам и применяют пороговые значения типа прожиточного минимума, в этой случае нет нормы, такой, что отклонение от нее в обе стороны указывало бы на проблемы.
Поскольку в случае дохода обычно исходят из допущения «чем больше, тем лучше», то среднее вполне применимо как статистика, дающая общую картину благосостояния. И если разница в средней температуре между двумя больницами ничего не говорит о том, где состояние больных лучше, разница в средней зарплате персонала этих больниц позволяет судить о различии в благосостоянии между ними.
Когда ссылаются на «среднюю температуру» в контексте экономических показателей, нередко имеют в виду что-то правильное, но неудачно выраженное с помощью неподходящей аналогии. В случае доходов указывают на большой разброс, при котором большие средние значения могут выходить за счет сверхдоходов небольшой кучки богатых. Если, допустим, в коллективе из ста человек все получают по 10 тыс., кроме начальника, получающего миллион, средний доход выйдет ок. 20 тыс. Рядовой член коллектива, увидев эту цифру, может в ней усомниться, поскольку она вдвое выше зарплаты, которую получает он и его коллеги.
Вместо среднего можно использовать другой показатель благосостояния, лишенный этого изъяна, медиану – величину, которая делит выборку пополам. В нашем примере, ее значение будет равно 10 тыс., и оно как раз точно отразит уровень дохода, на который может рассчитывать рядовой член коллектива. Но у этого показателя имеются свои недостатки. Будучи хорош для характеристики середины, он ничего не говорит о том, что происходит на краях, а они тоже имеют значение.
Если с коллективом из примера выше мы сравним другой коллектив из ста человек, в котором все получают по 10 тыс., ни среднее, ни медиана не дадут полного представления о разнице в доходах между ними. Если отталкиваться от среднего, мы можем ошибочно подумать, что в первом коллективе получают вдвое больше, а если будем отталкиваться от медианы, то, опять же, ошибочно решим, что эти коллективы одинаково бесперспективны в плане потенциального роста доходов.
Но отсюда следует не бесполезность статистики, как некоторые заключают, а лишь недостаточность любого отдельно взятого показателя как характеристики благосостояния. Конкретный показатель – это штрих к портрету, но не сам портрет, для прорисовки которого требуется множество штрихов в совокупности.
Резюмирую: статистика как «худшая ложь» может выступать лишь в неумелых руках, но этим она не отличается от всех прочих сфер человеческой деятельности, будь то лечение людей, управление государством или игра на гитаре.
Средняя температура по больнице
Есть три вида лжи: ложь, гнусная ложь и статистика.
Применимо как намёк на невозможность усреднения всего подряд.
Содержание
Что это
— Какова средняя температура больных в энской больнице?
— 36,6 °С, включая гнойное и морг!
Статистику всегда можно притянуть для доказательства или опровержения чего угодно, но не всегда это будет достоверно — особенно когда в выборку попадают абсолютно непохожие элементы — тогда вычисление среднего теряет всякий смысл. Среднее всегда должно вычисляться среди схожих параметров.
Получившееся усреднение «36,6», куда попали и лихорадящие больные и пациенты морга с температурой холодильника, не даёт возможности для достоверных выводов: «один бьётся в горячке, другой остывает в морге, а средняя температура по больнице 36,6 °C.».
Как этим работать
Статистик утонул переходя реку, средняя глубина которой составляла всего лишь 1 метр.
Председатель колхоза делает доклад перед коллективом: — За истёкший период урожай пшеницы в среднем составил 5 тонн с гектара, картошки — 3 тонны с гектара…
Одна баба поднимает руку.
— Товарищ председатель, а как это, «в среднем»?
— Ну, вот если, скажем, одна корова даёт 4 литра молока в день, а другая — 6, то в среднем они дают по 5.
— Это что же получается?! У меня, значит, один джентльмен, у Люськи их трое, у Машки — пятеро, а в среднем я тоже блджадь?!
В больнице
А в больницах таки иногда используется средняя температура по больнице, в которой можно наглядно увидеть процент лихорадящих больных во время эпидемий. Морг в выборку таки не входит.
Средняя температура по больнице. Что значит это выражение?
Это медики придумали.Приходит ревизия, как больные?, а им всё в ажуре. Вот статистика. У больных в среднем температура 36,6.Проверяющие смекнули! А потом врачи к ним приходят, говорят зарплата низкая, у санитарок 3-4 т.р.. А им-всё в ажуре, ваша зарплата в среднем, включая главврачей 36 тысяч 600 рублей.
Другой вариант этой присказки: река в среднем была мелкая, но лошадь утонула.
Русский писатель и драматург Иван Щеглов (псевдоним И.Л. Леонтьева) опубликовал сборник рассказов под общим названием «Дачный муж», по всей вероятности, принадлежащим одному из рассказов (не читала, определенней сказать не могу).
Но широко известным и крылатым выражение дачный муж стало не сразу и не ему самому благодаря. Помогла дружба с А.П. Чеховым, который использовал это словосочетание в своих рассказах, и оно получило дальнейшее распространение.
О чем же речь? Кто такой дачный муж?
Так называют человека, который должен каждый божий день возвращаться после службы в городе на дачу, где отдыхает его семья.
Каждое утро он получает множество поручений (и не только от своих родственничков, надо полагать), а вечером возвращается, нагруженный как верблюд, покупками по заказу. Естественно, ему приходится побегать по магазинам, а потом тащить чуть ли не в зубах эти многочисленные покупки.
Получается, что дачная жизнь превращается для него не в отдых, она приносит одни заботы и неприятности.
К этому человеку и прилипло, как кличка, имя дачный муж.
Это нарицательное звание для любого супруга, которому приходится жить такой жизнью хлопотной.
Иногда это крылатое выражение употребляется и просто в шутливом тоне, с ироническим оттенком.
Черная или белая это все таки зависть добрые намерения она не несет. Утверждение «Белая ворона» я думаю придумали завистливые люди. Кто чаще всего добивается успеха в жизни, только те люди, которые не похожи на других, мыслящие по другому, с определенной харизмой, которой у других нет. К сожалению выдержать шквал зависти в свой адрес не у всех получается, кто становится лебедем, а кто то действительно остается только «белой вороной» для радости завистников.
5 вариантов среднего или какая средняя температура в больнице?
Средняя температура по больнице — очень лукавое число, хотя сам термин «среднее значение» кажется нам очень простым. И именно простота делает его таким лукавым. Поговорим о том, какими, вообще, бывают средние значения, где и как их правильно применять.
Простой пример: Вы утром, спросонья, едите на своей машине в университет со скоростью 30 км/ч, потому как особого желания нет, но обратно ваша скорость уже 60 км/ч, потому как попасть домой спешите. Какова средняя скорость ваших перемещений за день?
Подсказка: Нет, это не 45 км/ч.
А пока вот вам небольшая табличка с названиями «средних», формулами их расчета и способами использования. Собственно, это план последующего изложения, оглавление.
Что это значит?
Начнём сначала. Что для нас значит слово «среднее»? Для большинства — это «что-то посередине» или число сбалансированное по некоторым показателям.
Можно предложить более универсальную интерпретацию понятия «среднее значение». Среднее значение какого-либо ряда значений — это некая простая оценка, которой можно охарактеризовать весь ряд, при этом, заменяя ей любой элемент ряда получим тот же результат. Условно говоря, можно выбросить все представленные данные, кроме среднего значения, а общий смысл числового ряда, что-то там характеризующего, не изменится.
Одна из целей получения среднего значения — понять суть выборки данных с помощью репрезентативного образца. Однако, процесс вычисления среднего значения определяется характером взаимодействия элементов выбранной группы данных. Посмотрим, что при этом происходит.
Среднее арифметическое
Среднее арифметическое знакомо всем со школьной скамьи:
Задачка: своими кровными 75 кг Вы нагрузили лифт вместе с подростком, весом 50 кг, и толстяком, весом 175 кг. Каков средний вес вашей весёлой компании?
На самом деле вопрос стоит чуть не так: Если заменить вашу весёлую компанию тремя серенькими клонированными людьми с одинаковым весом, то каким весом должен обладать каждый такой клон?
На фабрике по производству человеческих клонов надо просто заказать три экземпляра весом по 100 кг каждый (Мы уже посчитали: \frac<75 + 50 175> <3>) и довольно потирать руки.
Прелести среднего арифметического:
Изъяны среднего арифметического:
Закон Парето એ гласит, что «20% усилий дают 80% результата, а остальные 80% усилий — лишь 20% результата». Так и к нас среднее арифметическое срабатывает в 80% случаев, но к нашему глубокому сожалению, оставшиеся 20% случаев вынуждают нас искать альтернативы для подсчёта среднего значения и требуют очень значительных усилий при интерпретации.
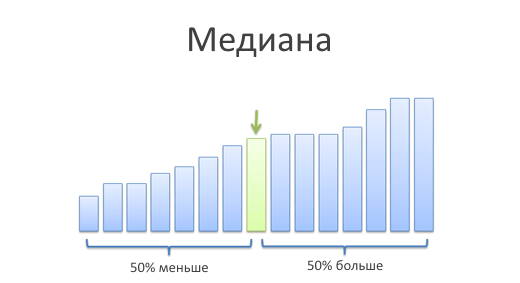
Медиана
Медиана — та самая грань, которая отделяет наибольшие значения от наименьших. То самое «число в середине». Постойте-постойте, а разве среднее арифметическое делает не то же самое?
Вот вам простой пример. Какое число находится в середине этого ряда?
Число «3» находится в середине ряда. И хотя среднее арифметическое (22) является «средним», оно никак не отражает распределения этих чисел. Интуитивно (и абсолютно правильно!) мы считаем, что в середине этого ряда всё-таки 3, а не 22. Здесь среднее значение отошло от середины благодаря резко отклоняющемуся из общей массы значению, 100.
Медиана эту проблему решает. Медиана делит весь числовой ряд на две равные части по количеству значений, причём первая половина имеет значения меньше либо равные медиане, а вторая — больше либо равные. Если в середине числового ряда оказывается два числа то, тобы получить медиану мы просто берём среднее арифметическое этих двух чисел. В числовом ряду 1, 2, 3, 4 медианой станет число 2,5. Именно медиана позволяет выбивающимся из общей массы числам вроде 100 в нашем примере выше не влиять на общее впечатление о числовом ряде.
Прелести медианы:
Изъяны медианы:
Такие средние значения, как цены на недвижимость или, например, уровень дохода часто вычисляются именно по медиане, потому что нам важна именно средняя стоимость большей части домов в конкретном районе или средний уровень доходов большей части населения. В таком случае Билл Гейтс с годовым доходом в несколько миллиардов не испортит нам всю статистику. Видите, как много зависит от того, как мы работаем с имеющимися данными?
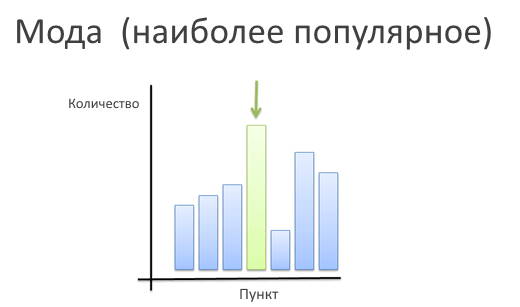
Мода એ (фр. mode, от лат. modus — мера, образ, способ, правило, предписание) — временное господство определённого стиля в какой-либо сфере жизни или культуры. Само слово может звучать странно для аналитика, но оно означает всего лишь наиболее часто встречающийся элемент в группе. На практике обычно мода определяется путём опросов и сбора мнений. Да, действительно порой бывают случаи, когда лучшим способом получить наиболее репрезентативный образец данных является сбор откликов.
Допустим, вы планируете вечеринку и нужно назначить день недели для её проведения. Дни недели — такой же числовой ряд, как и любой другой. Это всего лишь числа от 1 до 7. Среднее арифметическое и медиана тут не помогут (Лиза и Паша могут в пятницу, а Коля и Петя — в воскресенье; поэтому назначим субботу). Что делать? Конечно, выбрать тот день недели, который выберет большинство, ну а остальные либо подстроятся, либо не придут — демократия, однако.
Как правило, мода используется для получения наиболее репрезентативного значения в нечисловых рядах. Популярные цвета сезона, хиты продаж, рейтинги фильмов и музыки, лучшие кафе и закусочные определяются именно модой (чувствуете корреляцию со словом мода એ в его бытовым смысле).
Прелести моды: Прекрасно работает для получения представления об общественном мнении; Даёт представление о потребностях большой части людей (там, где среднее арифметическое даёт лишь осечку); Проста для понимания.
Изъяны моды: Для её вычисления требуется больше усилий (нужно собрать мнения и обработать их); Победителю достаётся всё: мода выявляет только одного лидера.
Среднее геометрическое
Наш «репрезентативный элемент» зависит от того, что мы делаем с уже существующими элементами группы данных. В большинстве случаев элементы просто складываются и среднее арифметическое работает прекрасно. Но иногда нужно нечто большее. Например, когда мы анализируем инвестиции, площади и объёмы. В таких случаях между собой данные взаимодействуют именно путём умножения (ожидаемая доходность, объём или площадь фигуры вычисляются с помощью умножения), и это меняет подход к выявлению и смыслу средних значений.
Вот пример. Какой инвестиционный портфель вы предпочтёте? Иными словами, какой из них принесёт большую прибыль в течение типового года?
Выглядят похоже. Повседневная логика, построенная на привычке к среднему арифметическому, говорит, что оба портфеля достаточно рискованны и оба в среднем приведут к убыткам или нулевой прибыли. Поэтому, вероятнее всего, надо выбрать портфель Б, поскольку в успешный год он принесёт больше прибыли.
Но это в корне неверно! На фондовом рынке с таким подходом мы с вами точно прогорим. Проценты с инвестиций умножаются, но не складываются. Мы не можем просто взять и использовать среднее арифметическое, нужно найти действительный коэффициент окупаемости. Коэффициент окупаемости считается достаточно просто: берём условные 100% нашего текущего капитала в качестве единицы. Далее представляем колебания доходности-убытка, представленные в описании портфелей, добавляя к нашей единице или вычитая из неё процентные показатели. Затем перемножаем полученные колебания и получаем коэффициент. Для расчёта среднегодового значения коэффициента окупаемости делим полученный коэффициент на 4 (поскольку элементов в нашем числовом ряду четыре).
Коэффициент окупаемости: 1,1 \times 0,9 \times 1,1 \times 0,9 = 0,98 (2% убытка)
Среднегодовое значение: 0,98^ <1>= 0,5\% годового убытка
Коэффициент окупаемости: 1,3 \times 0,7 \times 1,3 \times 0,7 = 0,83 (17% убытка)
Среднегодовое значение: 0,83^ <1>= 4,6\% годового убытка
Выбор между 2% или 17%? Огромная разница! Конечно, только идиот, а не разумный человек будет делать выбор именно из этих двух портфелей, но если делать выбор, то из двух зол лучше выбрать Портфель А. И именно здесь среднее арифметическое не работает.
Несколько примеров, где работает среднее геометрическое:
Среднее геометрическое помогает найти «типичный элемент» среди группы элементов, взаимодействующих друг с другом путём умножения. И, как видим, у него есть множество практических применений.
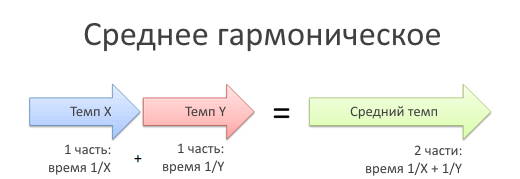
Среднее гармоническое
Среднее гармоническое представить сложнее, чем предыдущих представителей «средних», но оно не менее полезно. Между прочим, само понятие «гармоники» в математике связано с обратными числами (1/2, 1/3 и т.д.). Среднее гармоническое помогает нам вычислить среднее арифметическое в рядах чисел, заданных обратными значениями. Это бывает чаще, чем можно подумать.
Например, если я еду со скоростью 30 км/ч, это значит, что я получаю определённый результат (30 км) за какую-либо единицу времени (1 час). Когда мы хотим узнать среднее значение для нескольких скоростей (Х и Y), нужно думать о результате и единицах измерения, а не об исходных цифрах.
Возьмём двух сотрудников: Х и Y. Оба работают в одном проекте и выполняют одинаковое количество работы, но скорость их работы разная. Какова средняя скорость их работы?
Допусти, каменщик Х кладёт 30 кирпичей в час, а каменщик Y — 60 кирпичей в час. Значит, на один кирпич у каждого каменщика уходит:
Складываем результаты и единицы измерения:
Общий результат: 2 кирпича (Х и Y уложили по одному) Общая единица времени: 1/X + 1/Y (у каждого уходит разное количество времени)
Средней скоростью обоих каменщиков будет:
Если бы у нас было 3 каменщика (X, Y и Z), их средняя скорость вычислялась бы по формуле:
Здорово же иметь одну формулу вместо того, чтобы каждый раз заниматься долгими вычислениями. Даже вычисляя среднюю скорость 5 нерадивых работников стало бы головной болью. Помните наш первый пример про скорость, с которой вы едете на работу и домой? Чтобы найти среднюю скорость передвижения в тот день, мы просто используем формулу.
При этом нам даже не нужно знать, где находится дом или офис! Теперь вместо X и Y у нас не кирпичи, а количество километров за единицу времени. Вне зависимости от расстояния результат один и тот же: допустим, некое количество километров R мы проходим на скорости X, а другое количество километров R — на скорости Y. Средняя скорость при этом будет вычисляться так же, как вычисляется средняя скорость прохождения 1 км на скорости X и одного километра на скорости Y:
Ключевая идея: Среднее гармоническое используется тогда, когда один и тот же объём работы выполняется с разной производительностью.
Ещё более ключевая идея: Помните, что среднее значение — это один элемент, способный передать суть целой группы элементов. В нашем примере с работой и офисой в среднем туда-обратно мы едем на скорости 40 км/ч (вместо 30 км/ч туда и 60 км/ч обратно). Важно помнить, что средней скоростью мы заменяем каждую «стадию».
Ещё несколько примеров из жизни среднего гармонического:
В чём фокус?
Среднее гармоническое действительно не самая очевидная вещь. Дело в том, что если бы у вас было две разных установки, одна из которых работает со скоростью 10 деталей/час, а другая — 20 деталей/час, конечно, их средняя производительность составляла бы 15 деталей/час. В этом случае вы имеете полное право просто сложить их производительность и вычислить среднее арифметическое, ведь установки работают независимо друг от друга.
Если не верите в среднее гармоническое, можно устроить себе обратную проверку. Мы утверждаем, что наша универсальная установка по заготовке и полировке деталей справляется с 7,14 деталями в час. Проверим: мы знаем, что за час машина либо обрабатывает 25 деталей, либо полирует 10. Получаем:
Подготовка: 7,14/25 = 0,29 часов Полировка: 7,14/10 = 0,71 часов
Да-да, 0,29 + 0,71 = 1, цифры работают: для полного цикла изготовления 7,14 деталей действительно требуется один час.
Краткое резюме
Даже такая простая на первый взгляд идея, как «среднее значение», имеет массу применений. Здесь мы рассмотрели лишь самые основные и не затронули средневзвешенное, центр тяжести, математическое ожидание и многое другое. Но поняли главное: