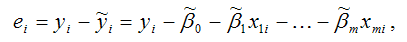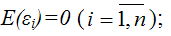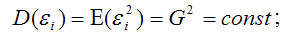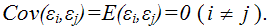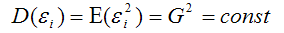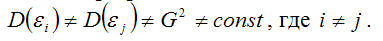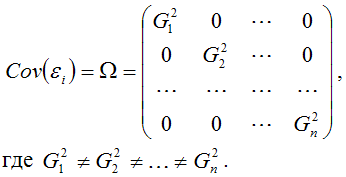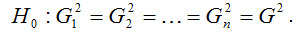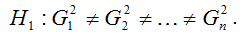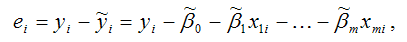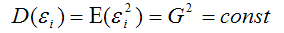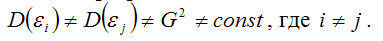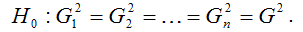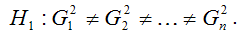Гетероскедастичность остатков для регрессионной модели означает что она имеет
Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:
В связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается выборочная оценка случайной ошибки модели регрессии по формуле:
где ei – остатки модели регрессии.
Термин гетероскедастичность в широком смысле понимается как предположение о дисперсии случайных ошибок модели регрессии.
При построении нормальной линейной модели регрессии учитываются следующие условия, касающиеся случайной ошибки модели регрессии:
6) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
7) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
8) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
означает гомоскедастичность (homoscedasticity – однородный разброс) дисперсий случайных ошибок модели регрессии.
Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки βi является известной постоянной величиной для всех наблюдений.
Но на практике предположение о гомоскедастичности случайной ошибки βi или остатков модели регрессии ei выполняется не всегда.
Под гетероскедастичностью (heteroscedasticity – неоднородный разброс) понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии:
Гетероскедастичность можно записать через ковариационную матрицу случайных ошибок модели регрессии:
Тогда можно утверждать, что случайная ошибка модели регрессии βi подчиняется нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2Ω:
где Ω – матрица ковариаций случайной ошибки.
Если дисперсии случайных ошибок 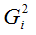
Для обнаружения гетероскедастичности остатков модели регрессии необходимо провести их анализ. При этом проверяются следующие гипотезы.
Основная гипотеза H0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:
Альтернативная гипотеза H1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:
Гетероскедастичность остатков модели регрессии может привести к негативным последствиям:
1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;
2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.
57. Гетероскедастичность остатков модели регрессии
57. Гетероскедастичность остатков модели регрессии
Случайной ошибкой называется отклонение в линейной модели множественной регрессии:
В связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается выборочная оценка случайной ошибки модели регрессии по формуле:
где ei – остатки модели регрессии.
Термин гетероскедастичность в широком смысле понимается как предположение о дисперсии случайных ошибок модели регрессии.
При построении нормальной линейной модели регрессии учитываются следующие условия, касающиеся случайной ошибки модели регрессии:
6) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:
7) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:
8) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):
означает гомоскедастичность (homoscedasticity – однородный разброс) дисперсий случайных ошибок модели регрессии.
Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки ?i является известной постоянной величиной для всех наблюдений.
Под гетероскедастичностью (heteroscedasticity – неоднородный разброс) понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии:
Гетероскедастичность можно записать через ковариационную матрицу случайных ошибок модели регрессии:
Тогда можно утверждать, что случайная ошибка модели регрессии ?i подчиняется нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2?:
где ? – матрица ковариаций случайной ошибки.
Если дисперсии случайных ошибок
модели регрессии известны заранее, то проблема гетероскедастичности легко устраняется. Однако в большинстве случаев неизвестными являются не только дисперсии случайных ошибок, но и сама функция регрессионной зависимости y=f(x), которую предстоит построить и оценить.
Для обнаружения гетероскедастичности остатков модели регрессии необходимо провести их анализ. При этом проверяются следующие гипотезы.
Основная гипотеза H0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:
Альтернативная гипотеза H1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:
Гетероскедастичность остатков модели регрессии может привести к негативным последствиям:
1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;
2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии
14. Оценка коэффициентов модели парной регрессии с помощью выборочного коэффициента регрессии Помимо метода наименьших квадратов, с помощью которого в большинстве случаев определяются неизвестные параметры модели регрессии, в случае линейной модели парной регрессии
15. Оценка дисперсии случайной ошибки модели регрессии
15. Оценка дисперсии случайной ошибки модели регрессии При проведении регрессионного анализа основная трудность заключается в том, что генеральная дисперсия случайной ошибки является неизвестной величиной, что вызывает необходимость в расчёте её несмещённой
18. Характеристика качества модели регрессии
18. Характеристика качества модели регрессии Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.Для оценки качества модели регрессии используются специальные показатели.Качество линейной модели парной регрессии
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом
35. Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом Проверка значимости коэффициентов регрессии означает проверку основной гипотезы об их значимом отличии от нуля.Основная гипотеза состоит в предположении о незначимости
39. Модели регрессии, нелинейные по факторным переменным
39. Модели регрессии, нелинейные по факторным переменным При исследовании социально-экономических явлений и процессов далеко не все зависимости можно описать с помощью линейной связи. Поэтому в эконометрическом моделировании широко используется класс нелинейных
40. Модели регрессии, нелинейные по оцениваемым коэффициентам
41. Модели регрессии с точками разрыва
41. Модели регрессии с точками разрыва Определение. Моделями регрессии с точками разрыва называются модели, которые нельзя привести к линейной форме, т. е. внутренне нелинейные модели регрессии.Модели регрессии делятся на два класса:1) кусочно-линейные модели регрессии;2)
44. Методы нелинейного оценивания коэффициентов модели регрессии
44. Методы нелинейного оценивания коэффициентов модели регрессии Функцией потерь или ошибок называется функционал вида Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии
46. Проверка гипотезы о значимости нелинейной модели регрессии. Проверка гипотезы о линейной зависимости между переменными модели регрессии На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все
58. Тест Глейзера обнаружения гетероскедастичности остатков модели регрессии
58. Тест Глейзера обнаружения гетероскедастичности остатков модели регрессии Существует несколько тестов на обнаружение гетероскедастичности остатков модели регрессии.Рассмотрим применение теста Глейзера на примере линейной модели парной регрессии.Предположим, что
59. Тест Голдфелда-Квандта обнаружения гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии
60. Устранение гетероскедастичности остатков модели регрессии Существует множество методов устранения гетероскедастичности остатков модели регрессии. Рассмотрим некоторые из них.Наиболее простым методом устранения гетероскедастичности остатков модели регрессии
61. Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция
61. Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция Автокорреляцией называется корреляция, возникающая между уровнями изучаемой переменной. Это корреляция, проявляющаяся во времени. Наличие автокорреляции чаще всего
62. Критерий Дарбина-Уотсона обнаружения автокорреляции остатков модели регрессии
62. Критерий Дарбина-Уотсона обнаружения автокорреляции остатков модели регрессии Помимо автокорреляционной и частной автокорреляционной функций для обнаружения автокорреляции остатков модели регрессии используется критерий Дарбина-Уотсона. Однако данный критерий
63. Устранение автокорреляции остатков модели регрессии
63. Устранение автокорреляции остатков модели регрессии В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков
67. Модели регрессии с переменной структурой. Фиктивные переменные
67. Модели регрессии с переменной структурой. Фиктивные переменные При построении модели регрессии может возникнуть ситуация, когда в неё необходимо включить не только количественные, но и качественные переменные (например, возраст, образование, пол, расовую
Гетероскедастичность
Опубликовано 27.06.2021 · Обновлено 27.06.2021
Что такое Гетероскедастичность?
В статистике гетероскедастичность (или гетероскедастичность) возникает, когда стандартные отклонения прогнозируемой переменной, отслеживаемые по различным значениям независимой переменной или относящиеся к предыдущим периодам времени, непостоянны. В случае гетероскедастичности контрольным признаком при визуальном осмотре остаточных ошибок является то, что они будут иметь тенденцию со временем расширяться, как показано на изображении ниже.
Гетероскедастичность часто возникает в двух формах: условной и безусловной. Условная гетероскедастичность определяет непостоянную волатильность, связанную с волатильностью предыдущего периода (например, дневной). Безусловная гетероскедастичность относится к общим структурным изменениям волатильности, которые не связаны с волатильностью предыдущего периода. Безусловная гетероскедастичность используется, когда можно определить будущие периоды высокой и низкой волатильности.
Ключевые моменты
Краткая справка
Хотя гетероскедастичность не вызывает смещения оценок коэффициентов, она делает их менее точными; более низкая точность увеличивает вероятность того, что оценки коэффициентов дальше от правильного значения генеральной совокупности.
Основы гетероскедастичности
В финансах условная гетероскедастичность часто наблюдается в ценах акций и облигаций. Уровень волатильности этих акций невозможно предсказать ни на какой период. Безусловная гетероскедастичность может использоваться при обсуждении переменных, которые имеют идентифицируемую сезонную изменчивость, таких как потребление электроэнергии.
Что касается статистики, гетероскедастичность (также обозначаемая как гетероскедастичность) относится к дисперсии ошибок или зависимости рассеяния в пределах как минимум одной независимой переменной в пределах конкретной выборки. Эти вариации можно использовать для расчета погрешности между наборами данных, такими как ожидаемые результаты и фактические результаты, поскольку они обеспечивают меру отклонения точек данных от среднего значения.
Чтобы набор данных считался релевантным, большинство точек данных должно находиться в пределах определенного числа стандартных отклонений от среднего, как описано в теореме Чебышева, также известной как неравенство Чебышева. Это дает рекомендации относительно вероятности того, что случайная величина отличается от среднего.
В зависимости от количества указанных стандартных отклонений случайная величина имеет определенную вероятность присутствия в этих точках. Например, может потребоваться, чтобы диапазон двух стандартных отклонений содержал не менее 75% точек данных, которые будут считаться действительными. Распространенная причина отклонений, выходящих за рамки минимальных требований, часто связана с проблемами качества данных.
Типы гетероскедастичности
Безусловный
Безусловная гетероскедастичность предсказуема и может относиться к переменным, имеющим циклический характер. Это может включать более высокие розничные продажи, зарегистрированные в период традиционных праздничных покупок, или увеличение количества обращений в ремонт кондиционеров в теплые месяцы.
Изменения в пределах дисперсии могут быть напрямую связаны с возникновением определенных событий или прогнозных маркеров, если сдвиги традиционно не являются сезонными. Это может быть связано с увеличением продаж смартфонов с выпуском новой модели, так как активность является циклической в зависимости от события, но не обязательно определяется сезоном.
Гетероскедастичность также может относиться к случаям, когда данные приближаются к границе; где дисперсия обязательно должна быть меньше, так как граница ограничивает диапазон данных.
Условный
Условная гетероскедастичность непредсказуема по своей природе. Нет явных признаков, которые заставляли бы аналитиков полагать, что данные станут более или менее разбросанными в любой момент времени. Часто считается, что финансовые продукты подвержены условной гетероскедастичности, поскольку не все изменения можно отнести к конкретным событиям или сезонным изменениям.
Условная гетероскедастичность обычно применяется к фондовым рынкам, где сегодняшняя волатильность во многом связана с волатильностью вчера. Эта модель объясняет периоды постоянной высокой и низкой волатильности.
Особые соображения
Гетероскедастичность и финансовое моделирование
Гетероскедастичность – важное понятие в регрессионном моделировании, а в инвестиционном мире регрессионные модели используются для объяснения эффективности ценных бумаг и инвестиционных портфелей. Наиболее известной из них является Модель ценообразования капитальных активов (CAPM), которая объясняет эффективность акций с точки зрения их волатильности по отношению к рынку в целом. Расширения этой модели добавили другие переменные-предикторы, такие как размер, импульс, качество и стиль (ценность против роста).
Эти переменные-предикторы были добавлены, поскольку они объясняют или учитывают дисперсию зависимой переменной. Эффективность портфеля объясняется CAPM. Например, разработчики модели CAPM знали, что их модель не может объяснить интересную аномалию: высококачественные акции, которые были менее волатильными, чем акции низкого качества, имели тенденцию работать лучше, чем предсказывала модель CAPM. CAPM утверждает, что акции с более высоким риском должны превосходить акции с более низким риском. Другими словами, акции с высокой волатильностью должны превосходить акции с низкой волатильностью. Но качественные акции, которые менее волатильны, имели тенденцию работать лучше, чем прогнозирует CAPM.