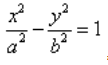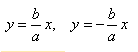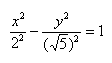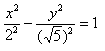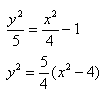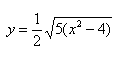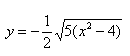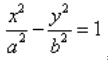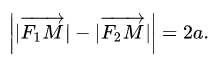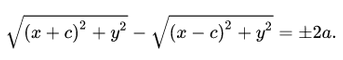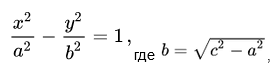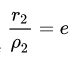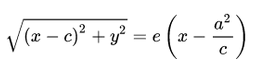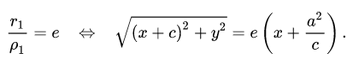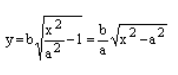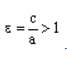Гипербола что это примеры
Что такое гипербола
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие гиперболы
Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы в алгебре выглядит так:
, где a и b — положительные действительные числа.
Кстати, канонический значит принятый за образец.
В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.
Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.
Вспомним особенности математической гиперболы:
Если гипербола задана каноническим уравнением, то асимптоты можно найти так:
Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:
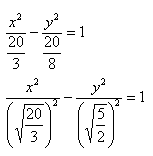
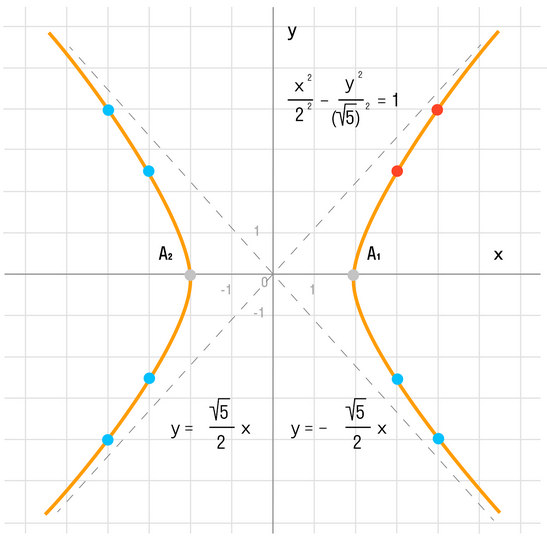
Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).
В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.
Способ такой же, как при построении эллипса. Из полученного канонического уравнения
на черновике выражаем:
Уравнение распадается на две функции:
— определяет верхние дуги гиперболы (то, что ищем);
— определяет нижние дуги гиперболы.
Далее найдем точки с абсциссами x = 3, x = 4:
Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.
Действительная ось гиперболы — отрезок А1А2.
Расстояние между вершинами — длина |A1A2| = 2a.
Действительная полуось гиперболы — число a = |OA1| = |OA2|.
Мнимая полуось гиперболы — число b.
В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.
Форма гиперболы
Повторим основные термины и узнаем, какие у гиперболы бывают формы.
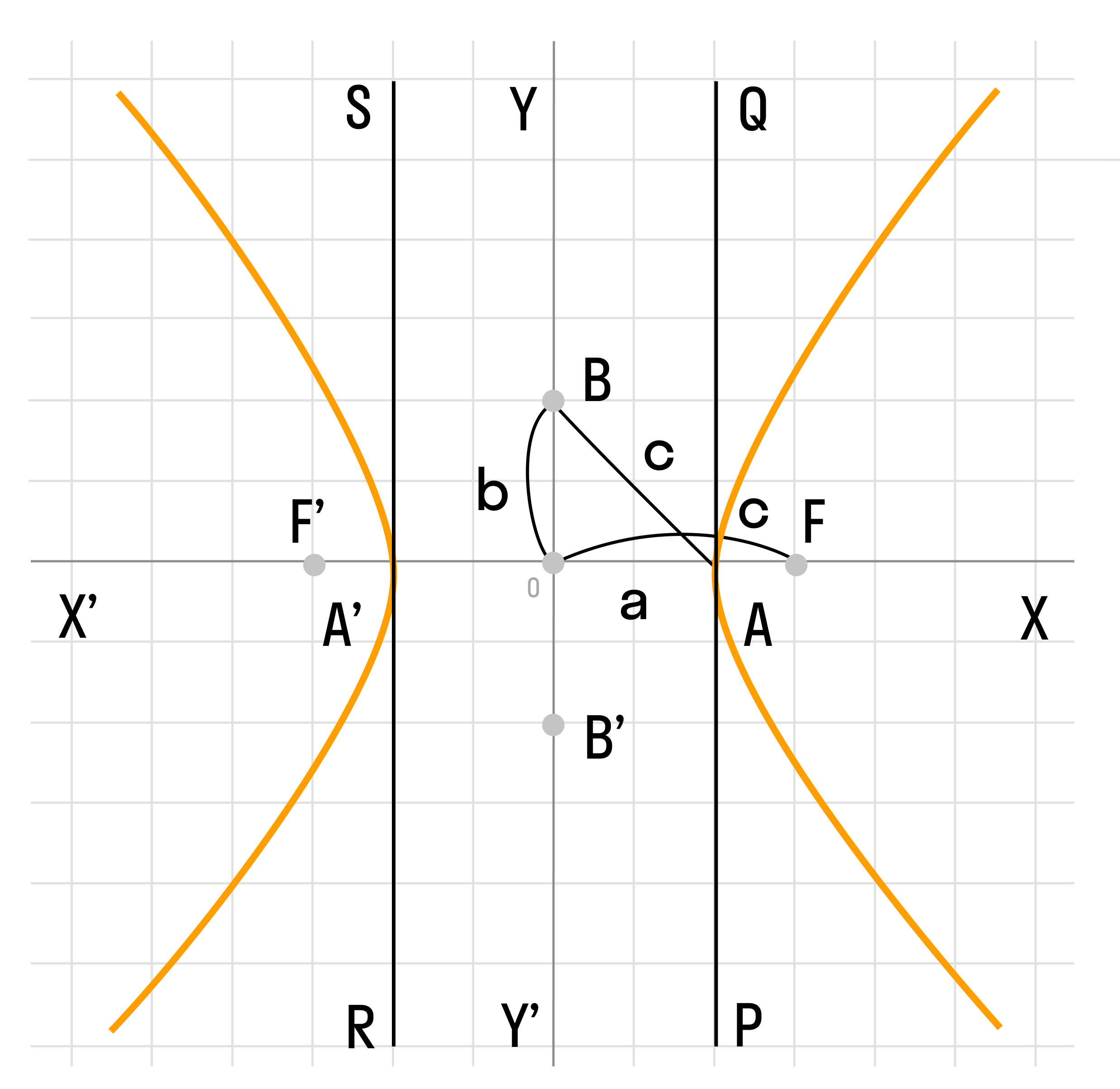
Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.
Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.
Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.
Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.
Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.
Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.
Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Фокальное свойство гиперболы
Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).
Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:
Рассмотрим, как это выглядит на прямоугольной системе координат:
Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:
Запишем это уравнение в координатной форме:
Избавимся от иррациональности и придем к каноническому уравнению гиперболы:
, т.е. выбранная система координат является канонической.
Директориальное свойство гиперболы
Директрисы гиперболы — это две прямые, которые проходят параллельно оси.
ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.
Директориальное свойство гиперболы звучит так:
Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.
Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
На самом деле для фокуса F2 и директрисы d2 условие
можно записать в координатной форме так:
Построение гиперболы
Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.
Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.
В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:
Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:
Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.
По определению эксцентриситет гиперболы равен
Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.
Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.
Что такое Гипербола в риторике
Гипербола (в риторике) — это стилистический приём, способ описания чего-либо с явным преувеличением, при котором кто-то или что-то представляется больше, лучше, ярче (и т. д.), чем в реальности. Например: 100 лет не виделись, горы трупов.
Слово гипербола пришло в русский язык из польского (hiperbola). Которое, в свою очередь, пришло из латинского (hyperbola — преувеличение) от греческого (ὑπερβολή) — буквально означает «бросок за пределы» (hyper — за предел, bole — бросок).
Примеры гиперболы в речи и литературе
Примеры в обиходе
Мы часто используем гиперболы в разговоре. Например:
Примеры из литературы
Но и писатели любят использовать этот приём преувеличения в своих литературных произведениях. Например:
«Редкая птица долетит до середины Днепра».
«Вечера на хуторе близ Диканьки», Н. В. Гоголь
«Чуден Днепр при тихой погоде. без меры в ширину, без конца в длину. «.
«Вечера на хуторе близ Диканьки», Н. В. Гоголь
«И сосна до звезды достает».
«За гремучую доблесть грядущих веков. «, О. Э. Мандельштам
Примеры гипербол в английском языке
“It was so cold, I saw polar bears wearing hats and jackets” (“Было так холодно: я видел белых медведей в шапках и куртках”);
“We’re so poor we don’t have two cents to rub together” (“Мы так бедны, что у нас нет и двух центов, чтобы потереть вместе”);
“His brain is the size of a pea” (“У него мозг размером с горошину”).
Разница между преувеличением и гиперболой
Преувеличение — это когда человек выходит за грани. Например, когда один человек ждёт другого на протяжении 15 минут и, дождавшись, он ему говорит: «Я тебя жду уже целый час!».
Гипербола же — это совершенно нереалистичное преувеличение. В нашем примере фраза была бы «Я тебя жду уже целый год!».
Тропы
Гипербола считается тропом. Троп — это выразительный оборот речи, в котором автор использует слово/выражение в переносном значении либо сопоставляет предметы и явления, которые каким-то образом переплетаются между собой по смыслу.
Главные виды тропов, которые существуют в русском языке:
Смотрите подробнее про Метафору и Эпитет.
Литота
Противоположностью гиперболе (в литературе) является литота.
Литота (от греч. litotes — простота) — это:
Эвфемизм
Эвфемизм (от греч. euphemeo — «говорю вежливо», eu — «хорошо» + phemi — «говорю») — это слово, словосочетание или выражение, которое используется для замены социально неудобных или неприемлемых слов/выражений. Например:
сто лет не виделись
напугать до смерти
накупили еды на год вперед
Гиперболическими могут быть целые персонажи и ситуации. Например, преувеличенно жадный помещик Плюшкин и другие персонажи поэмы Гоголя «Мертвые души».
Что такое литота?
В отличие от гиперболы, намеренное преуменьшение называется литота. Пример литоты: «Прелестный шпиц, не более наперстка!» (А.С. Грибоедов).
Зачем нужны гиперболы?
Гипербола помогает более резко выразить мысль, захватить внимание, подчеркнуть особую значимость предмета. Гипербола может добавить повествованию драматизма или сделать его комичным. Она показывает отношение автора к изображаемым явлениям.
Какими бывают гиперболы?
Количественные гиперболы содержат численные преувеличения: миллион дел, тысячу раз предупреждал.
Лексические гиперболы используют определенные слова: абсолютно непонятный текст, работа никуда не годится.
Метафорические гиперболы содержат метафору, переносящую свойства одного предмета на другой: океан любви, лес рук.
Примеры гиперболы
Быстрый как молния
Вечный спорщик
Горы мусора
Ждать целую вечность
Куча денег
Миллион извинений
Море слез
Объехала полмира
Сто раз говорил
Примеры гиперболы в русской литературе
В сто сорок солнц закат пылал. (В.В. Маяковский)
Во сне дворник сделался тяжелым, как комод. (И. Ильф, Е. Петров)
И подарю тебе Большой театр и Малую спортивную арену. (В.В. Высоцкий)
Комара за семь верст ловили. (М.Е. Салтыков-Щедрин)
Разливы рек ее, подобные морям. (М.Ю. Лермонтов)
Редкая птица долетит до середины Днепра. (Н.В. Гоголь)
Что такое гипербола, примеры из литературы и повседневной жизни


Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Все мы в жизни хоть раз говорили или слышали подобные выражение (а кто-то и не раз): ВЕЧНО ОПАЗДЫВАЕТЕ или СТО ЛЕТ НЕ ВИДЕЛИСЬ.
И мало кто задумывался, что эти фразы лишены какого-то здравого смысла. Так, человек просто не может «вечно опаздывать». И не может кто-то не видиться «сто лет», хотя бы потому, что люди редко так долго живут.
Подобные преувеличения в русском языке называются гиперболами и именно о них пойдет речь в этой публикации.
Примеры гиперболы в речи и литературе
Примеры в обиходе
Мы часто используем гиперболы в разговоре. Например:
Примеры из литературы
Но и писатели любят использовать этот приём преувеличения в своих литературных произведениях. Например:
«Редкая птица долетит до середины Днепра». «Вечера на хуторе близ Диканьки», Н. В. Гоголь
«Чуден Днепр при тихой погоде… без меры в ширину, без конца в длину…». «Вечера на хуторе близ Диканьки», Н. В. Гоголь
«И сосна до звезды достает». «За гремучую доблесть грядущих веков…», О. Э. Мандельштам
Примеры гипербол в английском языке
“It was so cold, I saw polar bears wearing hats and jackets” (“Было так холодно: я видел белых медведей в шапках и куртках”);
“We’re so poor we don’t have two cents to rub together” (“Мы так бедны, что у нас нет и двух центов, чтобы потереть вместе”);
“His brain is the size of a pea” (“У него мозг размером с горошину”).
Для чего нужна гипербола
Гипербола в литературе позволяет авторам передавать читателю свои эмоции, тем самым позволяя красочней представить ситуацию. Эти стилистические фигуры, которые достаточно просто отличить от любого другого речевого приема, нужны, чтобы привлечь внимание, позволить прочувствовать все эмоции, которыми хотел поделиться писатель.
Они освобождают читателя от рамок реальности и приписывают сверхъестественные характеристики природным явлениям и людям. Гипербола в литературе играет отнюдь не последнюю роль, так как она делает нашу речь более живой, и позволяет прочувствовать эмоциональное и душевное состояние рассказчика или автора текста.
Это позволяет им четко и правильно передать словесную атмосферу рассказа. Функция гиперболы как приема — придавать яркости, эмоциональности и убедительности тексту. Также ее часто используют писатели-юмористы для создания в своих произведениях комических образов для персонажей, позволяя фантазии читателя оживить их в своем воображении.
Тропы
Гипербола считается тропом. Троп — это выразительный оборот речи, в котором автор использует слово/выражение в переносном значении либо сопоставляет предметы и явления, которые каким-то образом переплетаются между собой по смыслу.
Главные виды тропов, которые существуют в русском языке:
Смотрите подробнее про Метафору и Эпитет.
Литота и её значение
Антоним гиперболы — литота, художественное преуменьшение. В своей разговорной речи люди постоянно пользуются и преувеличением и преуменьшением.
Не успеешь глазом моргнуть и жизнь пролетела. Когда ждёшь, секунда годами тянется. Талия тоненькая, тоньше тростинки.
Авторы пользуются литотой так же часто, как и гиперболой.
«Единица — вздор, единица-ноль, голос единицы тоньше писка.» (В. Маяковский.)
Гипербола и литота вместе с другими художественными приёмами делают русскую речь выразительной, красивой и эмоциональной.
Не пропустите: художественный прием сравнение в литературе и русском языке.
Гипербола в математике
Гипербола — это множество точек плоскости, для которых модуль разности расстояний от двух данных точек (F1 и F2 на рисунке, называемых фокусами гиперболы) — это величина постоянная и меньшая, чем расстояние между фокусами.
F1 и F2 — фокусы гиперболы.
Из определения гиперболы мы знаем, что модуль разности расстояний от фокусов гиперболы — это величина постоянная, это означает:
|MF1 − MF2| = константа; т. е. расстояние от (M до F1) минус (M до F2) всегда будет постоянной величиной (константой; постоянной; цифрой с определённым числовым значением).
Каноническое уравнение гиперболы
Каноническое уравнение гиперболы выглядит так:
где a и b — длины полуосей (действительной и мнимой); т. е. a = расстояние от 0 до а и b = расстояние от 0 до b, как показано на этом рисунке:
Примечание: уравнение аналогично каноническому уравнению эллипса: x²/a² + y²/b² = 1, разница в сложении вместо вычитания.
Эксцентриситет гиперболы
Эксцентриситет (обычно обозначаемый буквой е) показывает, насколько гипербола является «некривой», т. е. чем он ближе к 1, тем более вытянут её прямоугольник в направлении оси (меньше углы, образуемые асимптотами) и тем больше эта гипербола будет «растягиваться» вдоль своей действительной оси.
Эксцентриситет гиперболы всегда больше 1.
(величина отрезка F1F2 = 2c; c = расстояние от нуля до F1 и, соответственно, от нуля до F2 )
M — точка на кривой;
N — точка на директрисе (отрезок MN перпендикулярен директрисе).
Эксцентриситет (обозначамый буквой е) является соотношением MF1/MN и имеет формулу:
Увеличение и уменьшение в фантастических произведениях
Писатели, создавая художественный текст своего произведения, могут реалистично описывать жизнь, не прибегая к преувеличению или преуменьшению окружающих предметов. Но некоторые авторы преуменьшают или преувеличивают не только слова, но и предметы окружающего мира, создавая фантастический нереальный мир.
Ярким примером служит
сказка Льюиса Кэрролла «Алиса в Стране чудес». Героиня сказки попадает в такой мир, где она и все встречавшиеся ей герои меняют свои размеры. Такой приём нужен авторам, чтобы выразить свои мысли и взгляды на какие-то проблемы и подсказать пути их искоренения. Можно вспомнить «Гулливер в стране лилипутов» Джонатана Свифта.
Писатели с сатирической, романтической и героической направленностью в творчестве часто прибегают к фантастике. Она творческая, самобытная, придуманная автором, но основана на реальных социально-бытовых условиях жизни авторов. Писатель создаёт фантастическое произведение, но его ситуации перекликаются с реальными событиями.
Когда проходит социальная действительность, давшая повод создать это фантастическое произведение, то новому поколению уже не всё понятно, откуда появились такие фантастические вымыслы.
Интересно знать: Понятие синекдоха.
Гипербола и литота делают художественный текст выразительнее, помогают точнее передать эмоции. Без них творческое произведение было бы скучным и безликим. Не только авторы, но и обычные люди в повседневных разговорах не могут обойтись без них, хотя не знают их названий, а просто эмоционально выражают свои чувства и мысли.
Из художественных произведений
Нередко писатели используют гиперболу. Примеры из литературы довольно разнообразны. Так, очень часто к этому приему обращался Пушкин: «Все флаги в гости будут к нам».
Есть гиперболы в лирике Маяковского:
Можно привести несколько интересных примеров гиперболы в русском языке, когда преувеличение касается неодушевленных предметов: до небес баобабы, жало в километр.
Нередко для эффекта преувеличения поэт использует слова в переносном смысле: глыба, туша. Или же сочетания слов, которые по отдельности не обладают подобным свойством, но поставленные вместе создают гиперболизацию: очки-велосипеды, глаза два луга.
Пример гиперболы из литературы можно найти и в творчестве других писателей: «шаровары, шириной с Черное море» (Гоголь), «четыре года мы побег готовили, харчей три тонны мы наэкономили» (Высоцкий).
Мы рассмотрели, что такое гипербола, и примеры ее употребления мастерами слова. Этот прием дает возможность делать речь писателей образной и более выразительной, привлечь внимание читателя к какому-либо свойству или особенности описываемого предмета или лица. Также именно намеренное преувеличение нередко помогало автору выразить свое отношение к происходящему.
Каждый человек хоть раз сталкивался с понятием гиперболы в литературе. Но не каждый знает, что обозначает этот термин.
Гипербола — это стилистический прием, который применяется в литературе
Данным стилистическим приемом пользуются многие современные писатели и авторы.
Что такое гипербола
В математике, гипербола — это незамкнутая кривая с двумя ветвями.
В качестве приема в публицистике, гипербола — это преувеличение (например, говорить тысячу раз). Противоположностью гиперболы является литота (мужичок с ноготок).
что такое гипербола
Гипербола это математическая функция y=К/х (при К не равном нулю)
В разговорной речи гипербола это специальное сильное преувеличение чего либо для акцентирования на этом внимания собеседника.
есть несколько значений, но происхождение его общее, от древнегреческого слова, которое означает — переходить, избыточность, чрезмерность, преувеличение:
Гипербола — это множество точек плоскости, модуль разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.
Каноническое уравнение гиперболы в декартовых координатах
Слово гипербола имеет несколько значений. Первое значение — математическое. Согласно Эвклиду, гипербола это плоская кривая второго порядка, которая состоит из двух отдельных кривых, которые не пересекаются. Формула гиперболы У=К/х, при условии, что к не равно 0. Тоесть вершины гиперболы стремятся к нолю, но никогда не пересекаются с ним.
Второе значение — литературное. Гипербола это стилистическая фигура намеренного преувеличения.
Гипербола Математическая функция, которая строится на площади ХУ состоящая из 5 точек соединенных между собой и расположены на вертикальных четвертях ХУ. Формула y=K/x.
Так же значение этого слова литературе- преувеличение чего-либо, или ударение этого на внимание собеседника.
Давайте сразу определимся, что мы рассматриваем, гипербола с математической стороны или гипербола, как риторика. Давайте сначала рассмотрим с математической стороны:Линия состоящая из точек.Или как написано в одном источнике
Так же как эллипс и парабола, гипербола является коническим сечением.
А если рассмотрим со стороны риторики:Стилистическая фигура, для усиления выразительности.
quot;Гиперболquot; — математический термин означает плоскую кривую второго порядка. Значение quot;гиперболаquot; в литературе — преувеличение, для придания фразе выразительности,акцентировать внимание. Например выражение: quot;море слезquot;.
Гипербола (от греч. hyperbole — преувеличение). «Все большие произведения. — писал А.Горький, — все те произведения, которые являются образцами высокохудожественной литературы, покоятся именно на преувеличении, на широкой типизации явлений». Преувеличение и типизацию Горький уверенно и безошибочно ставит рядом, на собственном писательском и читательском опыте, понимая под этим способность и умение художника увидеть самое существенное в наблюдаемых явлениях, извлечь из них основной смысл, сгустить его силой воображения в художественный образ.
Преувеличение — «ядро» типизации.
Один из самых эффектных и эффективных приемов художественного преувеличения — гипербола в литературе. Она позволяет «представить непредставляемость», «соотнести несоотносимое», то есть наиболее остро и резко дать ту или иную деталь — в портрете, во внутреннем облике персонажа, в явлении объективного мира. Подчеркнем — объективного. Потому что, говоря о гиперболе, следует иметь в виду, что какой бы невероятной, какой бы фантастической она ни была, в основе ее всегда — жизненный материал, жизненное содержание.
Художественная убедительность и многозначность гиперболы тем весомее, чем яснее представляет себе читатель конкретную сущность образа или ситуации.
Так, один из главных персонажей гоголевского «Ревизора» Хлестаков сам о себе говорит, что у него «легкость необыкновенная в мыслях». В обществе, основанном на всеобщем чинопочитании, на всеохватном лицемерии, ложь Хлестакова, при всей ее гиперболической несуразности («как прохожу через департамент, — просто землетрясение, все дрожит и трясется как лист» и т.п.), принимается провинциальными чиновниками за чистую правду.
Еще пример. В романе Маркеса «Осень патриарха» рассказ о «тысячелетнем» патриархе ведется от «мы», и этот прием использования коллективной точки зрения, многоголосия, дает почувствовать и представить себе атмосферу слухов и недомолвок о герое. О диктаторе с самого начала ничего не известно наверняка — и до конца книги. Каждое новое толкование его поступков раскрывает лишь какую-либо одну из сторон его облика, где на первый план выдвигается исключительность, несходство с обыкновенными людьми. И это придает всему стилю повествования определенную гиперболичность.
Для создания гиперболического художественного образа используются различные виды тропов: сравнения, уподобления, метафоры, эпитеты и т.д. Функция их состоит в том, чтобы преувеличить предмет, наглядно раскрыть противоречие между содержанием и формой его, сделать изображение более впечатляющим, броским. К слову, ту же цель может преследовать и преуменьшение, литота, которую можно рассматривать как разновидность гиперболы, как гипербола в литературе «со знаком минус». В зависимости от социально-эстетической направленности произведения одно и то же событие может восприниматься как «гигантское» или же как «мелкое». В романе Д.Свифта «Путешествия Лемюэля Гулливера» гипербола и литота соседствуют: в первой части книги современная писателю Англия показана как бы через уменьшительное стекло, во второй — через увеличительное. В стране лилипутов волы и овцы до того крохотны, что герой сотнями грузит их в свою лодку. Под стать этим размерам и все прочее, с чем сталкивается Гулливер в этой стране, вплоть до социального уклада и политических событий. Сатирическим преуменьшением Свифт дает читателю понять, что претензии островной, «лилипутской», в сущности, Англии на мировое господство (на роль «владычицы морей», на обширные колониальные владения и проч.), казавшиеся многим англичанам великими, грандиозными, если задуматься, ничтожны и даже смешны.
Впечатляющ и другой гиперболический образ — из самого начала романа: герой приходит в себя после кораблекрушения и не может оторвать головы от земли — каждый волос его накручен на вбитый в землю «лилипутский» колышек. Здесь гипербола в литературе обретает символическое звучание, наводит на мысль о личности в неволе у множества ничтожных страстей и обстоятельств…
Именно в сатирическом произведении гипербола чаще всего уместна и художественно оправданна. В.Астафьев в «Царь-рыбе» с помощью этого приема выявляет внутреннее убожество одного из «любителей природы», браконьера Грохотало: «Рыбак Грохотало недвижной глыбой лежал за жарко нагоревшим костром. сотрясая берег храпом, как будто из утробы в горло, из горла в утробу перекатывалась якорная цепь качаемого волнами корабля». Здесь проступает авторская оценка персонажа с его ненасытно-агрессивным отношением к природе, персонажа, олицетворяющего бездушную серость. Однако гипербола в литературе, даже и «осмеивающая», может и не быть явно сатирической. Диапазон использования этого прима достаточно широк, охватывает и юмор, и иронию, и комизм.
Гиперболизируются — но уже сатирически — и образы противников былинных богатырей. Например, если Илья Муромец внешне ничем не отличается от окружающих, то его «супостат» Идолище — и ростом в «две сажени», и в плечах «косая сажень», и глазищи у него что «пивные чашищи», и нос что «локоть»… Благодаря этому контрастному внешнему сопоставлению победа богатыря выглядит особенно внушительной, заслуживающей народного прославления.
Литературные тропы — это художественные приёмы, слово или выражение, используемые автором для усиления выразительности текста и усиления образности языка.
В википедии говорится, что гипербола — это слово из греческого языка и обозначает преувеличение. Первая часть слова «гипер» есть во многих словах со значением преувеличения, превышения: гипертония, гипергликемия, гипертиреоз, гиперфункция.
Гипербола в литературе — это художественное преувеличение
. Кроме того, понятие гипербола есть в геометрии, и там она обозначает геометрическое место точек.
В данной статье будет идти речь о гиперболе с литературной точки зрения. Её определение, как давно она известна, кем и где употребляется. Она встречается повсюду: в литературных произведениях, в ораторских речах, в повседневных разговорах.
Самые простые примеры
Широко используется гипербола в русском языке. Примеры покажут, что нередко мы пользуемся этим приемом, даже не обращая внимания. Например, слова «Я тебе уже тысячу раз говорила!». В данном случае «тысяча раз» — это и есть преувеличение, ведь автор высказывания, во-первых, вряд ли говорила что-либо так много раз. Во-вторых, она не считала число своих повторов. Еще один пример гиперболы в русском языке: «Мы не виделись уже сто лет». Здесь речь идет о том, что люди не встречались длительный период времени, но уж никак не сотню лет.
Сказав, что у него миллион проблем, человек подчеркнет то, что у него сейчас черная полоса в жизни, а о четкой количественной характеристике проблем речь не ведется. Похожих примеров можно привести множество:
Нередко, сами не обращая внимания, мы употребляем гиперболу. Примеры в русском языке, приведенные выше, проиллюстрировали эту мысль.
Использование в литературе
Гиперболы в литературе
очень любят использовать все без исключения писатели. Делают они это для того, чтобы украсить свои произведения, сделав их более эмоциональными, яркими, наполненными.
И это совсем не удивительно, ведь без этой стилистической фигуры и ей подобных любое произведение было бы пустым, скучным и абсолютно неинтересным. Навряд ли такие произведения захватили бы внимание читателя, будоража его воображение, вызывая в нем многочисленные яркие эмоции.
Еще одно определение гиперболы – это преувеличение именно до неправдоподобности, поэтому очень важно помнить и иметь в виду, что её не нужно понимать буквально!
Как реализуется художественное преувеличение
Чтобы ясно понять, что такое гиперболы в литературе нужно знать способы реализации усиления, присущие тексту художественного произведения. Выразительность достигается писателем путем использования лексических гипербол, включающих слова «совершенно», «совсем», «все». Метафорический прием основан на образном сравнении. Фразеологические гиперболы в литературе представляют собой устойчивые выражения. Количественное усиление включает обозначение числа.
Лексические гиперболы
Выразительность создается в литературе путем использования определенных слов:
совсем скверно, совершенно непонятный почерк, никуда не годится, всем людям известно.
Метафорические гиперболы
Образный перенос содержат такие словосочетания: весь мир – театр, лес рук, безграничный океан любви, обещать золотые горы.
Фразеологические гиперболы
Устойчивыми выражениями являются следующие преувеличения:
козе понятно, побью как младенца, контракт дешевле бумаги, на которой он написан.
Количественные гиперболы
Численные преувеличения содержат такие выражения:
тысяча дел на вечер, миллион раз предупреждал, гора папок с бумагами.
Причина возникновения гиперболы
Сложно представить, что потребность в чрезмерном преувеличении зародилась еще в древние времена. Суждения людей современного общества разительно отличаются от мировоззрения древних людей, которые имели совсем фантастические представления о мире. В те далекие времена люди не могли иметь четкого понятия, что такое вымысел и реальность. Древнейшие люди наделяли волшебной силой те явления, которые не подавались объяснению. Они испытывали страх перед такими явлениями. Вследствие чего стали проявляться