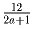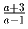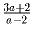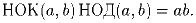найдите количество натуральных чисел n 6 1012 таких что нок 16 n 16n

Мне кажется, это должны быть нечётные числа, а их половина.

Тогда получается : 5 * 10 ^ 11.

Сумма двух натуральных чисел равна 500?

Сумма двух натуральных чисел равна 500.

Записать в в иде алгебраического выражения : 1)сумму двух последовательных натуральных чисел, меньшее их которых равно n 2)произведение двух последовательных натуральных чисел, большее из которых равн?

Найдите сумму всех натуральных n таких, что n больше или равно 1000 и НОК(128 ; n) = 128 * n?

Найдите сумму всех натуральных n таких, что n больше или равно 1000 и НОК(128 ; n) = 128 * n.

Сумма восьми натуральных чисел равна 2010?

Сумма восьми натуральных чисел равна 2010.

Какое наименьшее значение может принимать их НОК?

Ребят, помогите?

Я в этих НОК и НОД ничего не понимаю( Произведение двух натуральных чисел равно 120.

Найдите НОК этих чисел если НОД их равен 2.

Запишите все разные пары натуральных чисел, НОК которых равно 10?

Запишите все разные пары натуральных чисел, НОК которых равно 10.

Чему равна произведение всех натуральных чисел больше 7 и меньше 12?

Чему равна произведение всех натуральных чисел больше 7 и меньше 12.

Вычисли произведение удобным способом.

Сумма трех различных трехзначных чисел, два из которых меньше 800, равна равна 1775?

Сумма трех различных трехзначных чисел, два из которых меньше 800, равна равна 1775.

Найдите возможное наименьшее значение меньшего из этих чисел.

Сумма двух натуральных чисел меньше 18, а одно из чисел равно 14?

Сумма двух натуральных чисел меньше 18, а одно из чисел равно 14.

Чему может быть равно второе число?

Источник

Найдите количество натуральных чисел n 6 1012 таких что нок 16 n 16n

а) Найдите хотя бы одно такое натуральное число n, что десятичная запись числа n 2 + 2n оканчивается всеми цифрами числа n, записанными в том же порядке.

б) Может ли такое число оканчиваться цифрой 3?

в) Найдите все такие четырёхзначные числа

а) Например, число 9.

б) Предположим, что n = 10k + 3. Тогда

то есть десятичная запись числа n 2 + 2n оканчивается цифрой 5. Значит, такое невозможно.

в) Запишем условие задачи в таком виде: преобразуем:

т. е.

Если n ≠ 9999, мы должны подобрать два числа, одно из которых делится на 16, а другое на 625 и одно из которых больше другого на 1.

Переберём нечётные четырёхзначные числа, кратные числу 625: 1875, 3125, 4375, 5625, 6875, 8125, 9375. Из них только число 9375 имеет вид 16k − 1, а чисел вида 16k + 1 среди них нет.

Значит, искомое число может равняться 9375 или 9999.

Источник

Найдите количество натуральных чисел n 6 1012 таких что нок 16 n 16n

а) Приведите пример такого натурального числа n, что числа n 2 и (n + 16) 2 дают одинаковый остаток при делении на 200.

б) Сколько существует трёхзначных чисел n с указанным в пункте а свойством?

в) Сколько существует двухзначных чисел m, для каждого из которых существует ровно 36 трёхзначных чисел n, таких, что n 2 и (n + m) 2 дают одинаковый остаток при делении на 200.

а) Например, число 17.

б) Если два числа дают одинаковых остаток при делении на 200, то их разность будет делиться на 200. Имеем:

Следовательно, делится на 25, откуда Тогда:

Таким образом, существует 36 чисел.

в) По условию — целое, поэтому m — четное, т.е. Имеем:

— целое, m — двузначное, поэтому

1) Пусть k = 25, тогда n может быть любым трехзначным нечетным числом, которых гораздо больше, чем 36.

2) Пусть но кратно пяти. Значит, (n + k) кратно 10. В зависимости от k подойдут либо все четные трехзначные числа, делящиеся на 5, либо нечетные, делящиеся на 5. В любом случае таких чисел больше 36.

3) Пусть k не кратно 5, k — нечетное, но сумма (n + k) кратна 50. Поскольку то (n + k) с учетом условия принимает все значения, кратные 50, причем на одно значение — одно значение m. Следовательно, для каждого k возможно 18n, что не подходит по условию задачи.

4) Пусть k не кратно 5, k — четное, и сумма (n + k) кратна 25. Рассуждая аналогично пункту 3) при и возможных значений (n + k) — 36, поэтому возможных значений n тоже 36. При и возможных значений (n + k) — 36, поэтому возможных значений n тоже 36. В таблице представлены подходящие k и соответствующие им m. Их 18.

Источник

Найдите количество натуральных чисел n 6 1012 таких что нок 16 n 16n

Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1).

а) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 10 нулями?

б) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 17 нулями?

в) Сколько существует натуральных чисел n, меньших 75, для каждого из которых десятичная запись числа n! · (75 − n)! оканчивается ровно 17 нулями?

Раскладывая все числа от 1 до n на простые множители и объединяя затем множители 2 и 5 в пары, мы будем получать множители 10, которые просто прибавляют 0 на конце числа. Когда множители 2 или 5 (на самом деле всегда 5) закончатся, оставшееся число не будет кончаться на 0, поэтому количество нулей равно либо суммарному количеству пятерок, либо суммарному количеству двоек в разложении всех чисел от 1 до n на простые множители.

а) Пусть n = 45. Есть ровно 9 чисел кратных 5 от 1 до 45, при этом одно (25) содержит сразу две пятерки. Ясно, что 10 двоек наберется (там есть 22 четных числа, дающих минимум по одной двойке).

нулей. Заметим, что при целом k [α] + [k − α] = k при целом α и [α] + [k − α] = k − 1 при нецелом α, поэтому или 14 и или 2. Нас интересует вариант 15 + 2 (вариант 14 + 3 означал бы, что n не кратно 5, но кратно 25, что невозможно). Значит n кратно 5, но не 25. Таких чисел 12.

Отметим, что одно из чисел n или 100 − n не меньше 38, поэтому его факториал содержит не менее 19 четных множителей, так что двоек на все эти пятерки хватит.

Источник

Найдите количество натуральных чисел n 6 1012 таких что нок 16 n 16n

Задача 1: Существует ли такая тройка натуральных чисел, что любые два из них имеют общий делитель, больший единицы, но общим делителем для всех трёх чисел является только 1?

Задача 2: Можно ли монетами в 14 и 35 шиллингов заплатить без сдачи сумму в 1999 шиллингов?

Решение: Нельзя, так как 1999 не кратно НОД(14,35).

Задача 3: В банк можно положить за один раз 120 руб. или снять 300 руб. У кого-то есть 1000 руб. Какую наибольшую сумму кто-то может положить в банк за несколько раз?

Решение: 960. Оценка получается из делимости. Снять и положить можно только числа, делящиеся на 60 (120 = 60 × 2, 300 = 60 × 5), максимальное число, меньшее 1000 и делящееся на 60 – это 960. Пример: кладём 3 раза по 300, снимаем 2 раза по 120 и кладём 300.

Решение: НОД – это общая часть разложений.

Решение: НОК – это объединение разложений.

Задача 6: Про натуральные числа a и b известно, что 15a = 14b и что НОД (a,b) = 13. Найдите a и b.

Задача 7: Докажите, что для любых натуральных чисел a и b верно равенство

Задача 8: Докажите, что если a и b – натуральные числа (a > b), то НОД (a,b) = НОД (a – b,b)

Задача 9: Может ли наименьшее общее кратное двух натуральных чисел равняться их сумме?

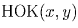
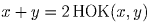
Решение: Пусть такие числа x и y существуют. делится на x и на y. Тогда x + y делится на x и на y, значит, x делится на y и y делится на x, поэтому x = y. Но тогда , что противоречит предположению.

Задача 10: Может ли наименьшее общее кратное трёх чисел равняться их сумме?

Решение: Да, например, 6 = 1 + 2 + 3.

Задача 11: НОД двух натуральных чисел в восемь раз меньше, чем их НОК. Докажите, что одно из этих чисел делится на другое.

Задача 12: Даны 6 натуральных чисел. Могут ли среди их попарных НОДов встречаться все натуральные числа от 1 до 15?

Решение: Нет. Так как какие-то числа имеют НОДы, равные 7 и 14, то есть не менее трёх чисел, кратных 7. Но тогда существует третий НОД, кратный 7, а среди чисел от 1 до 15 такого нет. (Аналогичное рассуждение проходит по делимости на 2).

Задача 13: Разность двух нечётных чисел является степенью двойки. Докажите, что они взаимно просты.

Решение: НОД (a,b) = НОД (a,a – b) = НОД (a,2 k ).

Задача 14: Известно, что (n – 1)! + 1 делится на n. Докажите, что число n – простое.

Решение: Если n – составное, то (n – 1)! делится на n.

Задача 15: В результате некоторой перестановки цифр число уменьшилось в три раза. Докажите, что исходное число делилось на 27.

Задача 16: Найдите все такие натуральные a, что число а) ; б) ; в) – тоже целое.

Источник