найдите все такие что числа простые укажите сумму всех таких чисел

Найдите все такие что числа простые укажите сумму всех таких чисел

Тема 5. Простые числа.

УПРАЖНЕНИЕ 1. а) Найдите все простые числа p, чтобы p-28 и p+40 тоже были простыми. б) Докажите, что остаток при делении любого простого числа на 30 не является составным числом.

Указание: а) при нечетных p и q четное число 5p+7q- составное, поэтому надо расматривать случаи, когда p=2 или когда q=2; б) при делении такого простого числа на 210 составными могут быть только остатки 11 × 11, 11 × 13 и 13 × 13 (обоснуйте!).

Тема 6. Элементы комбинаторики.

Ознакомимся с начальными сведениями комбинаторики в процессе решения упражнения.

УРАЖНЕНИЕ 2 . Имеется 5 различных книг и 3 различных журнала, которые расставляют соответственно на книжную полку и на полку для журналов.

а) Сколькими способами можно поставить на эти полки одновременно книгу и журнал?

б) Сколькими способами эти 5 книг можно поставить на книжную полку? Два способа расстановки считаем одинаковыми лишь в том случае, когда в результате расстановки каждым из них книги будут стоять на полке в одном и том же порядке.

в) Сколькими способами можно поставить 3 книги из 5 на книжную полку? Два способа расстановки считаем одинаковыми лишь в том случае, когда в результате расстановки каждым из них на полке будут одни и те же книги и в одном и том же порядке.

г) Сколькими способами можно поставить 3 книги из 5 на книжную полку? Два способа расстановки считаем одинаковыми лишь в том случае, когда в результате расстановки каждым из них на полке будут одни и те же книги.

д) Сколькими способами на эти полки можно поставить одновременно 3 книги и 2 журнала? Два способа расстановки считаем одинаковыми лишь в том случае, когда в результате расстановки каждым из них на полке будут одни и те же книги и журналы.

а) Поставим какую-то книгу на полку, одновременно с ней мы можем поставить на журнальную полку один из трех журналов, т.е. существует три способа расстановки, в результате которых на книжной полке будет выбранная книга. Поскольку книг 5 и для каждой из них имеем три способа расстановки, то всего существует 5 × 3=15 способов.

ЗАМЕЧАНИЕ . Допустим имеем n множеств элементов, а в каждом из этих множеств по элементов. Тогда число способов одновременного выбора по одному элементу из каждого из этих множеств равно (обоснуйте!). Так, например, в нашей задаче было n=2, и , поэтому число способов равнялось .

б) Первую книгу можно выбрать пятью способами, вторую- четырьмя (так как одна уже выбрана), третью- тремя (так как две книги уже выбраны), четвертую- двумя и последнюю пятую- одним способом. Откуда находим 5 × 4 × 3 × 2 × 1=120- общее число способов расстановки книг на полке.

в) Первую книгу можно поставить на полку пятью способами, вторую- четырьмя, а третью- тремя способами. Поэтому общее число способов равно 5 × 4 × 3=60.

ЗАМЕЧАНИЕ . Если имеется n элементов, то число упорядоченных наборов по k элементов () из этих элементов равно n × (n-1) × . × (n-k+1) (обоснуйте!). Такие упорядоченные наборы называются размещениями из n элементов по k, а их число обозначают , т.е. . Так, например, в нашей задаче было n=5 и k=3 и поэтому число способов равнялось

г) Обратите внимание на схожесть вопросов в заданиях в) и г)! Число размещений (упорядоченных наборов) из 5 книг по 3 равно . Но каждой тройке книг (неупорядоченному набору) соответствует 3!=1 × 2 × 3=6 перестановок из этой тройки книг. Поэтому искомое число неупорядоченных наборов по три книги равно , т.е. имеем 10 способов.

ЗАМЕЧАНИЕ . Если имеется n элементов, то число неупорядоченных наборов по k элементов () равно (обоснуйте!). Такие неупорядоченные наборы обычно называют сочетаниями из n элементов по k, а их число обозначают . Проверьте равенство: . Так, например, в нашей задаче было n=5 и k=3 и поэтому число способов равнялось .

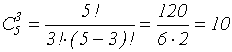
д) Сначала замечаем, что мы имеем дело с неупорядоченными тройками книг и парами журналов. Число способов выбора тройки книг равно , а число способов выбора пары журналов равно . Поэтому общее число способов равно 10 × 3=30 (самостоятельно это обоснуйте по аналогии с заданием а).

ЗАДАЧА 3. В классе 25 учащихся, среди которых 12 девочек. а) Учитель должен вызвать к доске одновременно мальчика и девочку. Сколькими способами он может это сделать? б) Нужно выбрать старосту класса и его заместителя. Сколькими способами это можно сделать? в) Для участия в конкурсе художественной самодеятельности нужно выбрать два мальчика и три девочки. Сколькими способами это можно сделать?

ЗАДАЧА 4. Имеется набор из 30 двузначных натуральных чисел.

а) Для каждой тройки чисел из набора нашли их сумму. Докажите, что среди полученных сумм найдется по крайней мере 16 равных между собой.

б) Указанный набор разбили на два набора, в одном из которых 10 чисел, а в другом 20 чисел. Затем нашли сумму каждой пары чисел, взятых по одному из каждого полученного набора. Докажите, что среди полученных сумм найдется по крайней мере две равные между собой.

в) Имея два набора как и в пункте б), нашли сумму каждой четверки чисел, в которой два слагаемых из одного набора, а остальные два слагаемых из другого набора. Докажите, что среди полученных сумм найдется по крайней мере 24 равных между собой.

Указание: а) опредилите число таких сумм и заметьте, что суммы могут принимать значения только от 30 до 297, а далее по принципу Дирихле; б) указанные суммы принимают значения от 20 до 198; в) указанные суммы принимают значения от 40 до 396.

УПРАЖНЕНИЕ 3. На доске написано число 876543210. За один ход разрешается стереть любые две цифры и вместо каждой из них написать большую или меньшую на 1 цифру. Можно ли за некоторое количество таких ходов получить на доске число 100000000?

Решение. Так как на доске за ход две цифры меняют свою четность на противоположную, то четность суммы цифр, записанных на доске, не меняется. Таким образом, в качестве инварианта можно рассматривать четность суммы цифр на доске. Так как у исходного числа суммы цифр 36 и является четной, то ни за какое число ходов мы не сможем получить число 100000000 с нечетной суммой цифр.

Тема 8. Построение циркулем и линейкой.

Желательно ознакомиться с содержанием §5 в учебнике по геометрии 7 И.Ф. Шарыгина и §4.2 в учебнике по геометрии 7-11 А.В. Погорелова. Как правило, оформление задач на построения циркулем и линейкой дается в виде алгоритма, состоящего из простейших построений. К простейшим построениям относятся: 1) откладывание на луче отрезка, равного данному; 2) деление отрезка пополам или проведение серединного перпендикуляра к отрезку; 3) построение перпендикуляра из данной точки на данную прямую; 4) построение на луче в данной полуплоскости угла, равного данному; 5) построение биссектрисы угла; 6) построение прямой, параллельной к данной прямой и проходящей через точку вне ее. Иногда в ходе построений можно ссылаться на некоторые опорные построения: 1) построение треугольника по двум сторонам и углу между ними; 2) построение треугольника по стороне и прилежащим к ней углам; 3) построение треугольника по трем сторонам; 4) построение треугольника, равного данному; 5) описать около треугольника окружность; 6) вписать в треугольник окружность; 7) провести касательную из внешней точки к окружности и пр ..

Сначала полезно решить две очень важные задачи (можно использовать учебник).

ЗАДАЧА 7. Докажите, что около треугольника можно описать и притом одну окружность.

Полезно знать два способа построения касательной из внешней точки к окружности (§4.2 в учебнике И.Ф. Шарыгина и §11 в учебнике А.В. Погорелова). Это поможет в решении некоторых из предлагаемых ниже задач, в которых имеются ввиду построения только с помощью циркуля и линейки.

ЗАДАЧА 9 . Постройте треугольник по двум сторонам и высоте к первой из этих сторон.

Указание: отметим, что по этим данным можно построить два разных треугольника.

Особую роль играет метод геометрических мест точек (см. §41 и §5 в указанных ранее учебниках)

ЗАДАЧА 10. В плоскости дан разносторонний треугольник АВС. Постойте ГМТ (геометрическое место точек), равноудаленных от точек В и С, а также от прямых АВ и АС.

ЗАДАЧА 12 . На данной прямой постройте все точки, из которых отрезки касательных к данной окружности равны данному отрезку.

Попробуйте решить следующие две задачи (первую из них приписывают Герону!).

ЗАДАЧА 13. В одной полуплоскости относительно прямой j даны две точки А и В. Опредилите на прямой j точку М такую, чтобы АМ + МВ было наименьшим. Постройте ее.

Источник

Найдите все такие что числа простые укажите сумму всех таких чисел

1. Из цифр 1, 2 и 5 составляют различные трёхзначные числа, в каждом из которых все цифры различны. Найдите сумму всех таких трёхзначных чисел. Ответ дайте в виде целого числа.

2. Найдите площадь прямоугольного треугольника, один катет которого на 2/3 больше другого и на 2/3 меньше гипотенузы. Ответ дайте в виде действительного числа, округлив его при необходимости стандартным образом до сотых. Целую и дробную части разделяйте точкой.

3. Убывающая последовательность a, b, c — геометрическая прогрессия, а последовательность 279a, 1535b/11 и c/11 — арифметическая прогрессия. Найдите знаменатель геометрической прогрессии. Ответ дайте в виде действительного числа, округлив его при необходимости стандартным образом до сотых. Целую и дробную части разделяйте точкой. Если решений нет, в ответ запишите 0.

5. Каков наибольший объём пирамиды SABC, у которой AB=5, AC=8 и sin∠BAC=45, а все боковые рёбра SA,SB,SC образуют с плоскостью основания одинаковые углы, не превышающие 60∘? Ответ дайте в виде действительного числа, округлив его при необходимости стандартным образом до сотых. Целую и дробную части разделяйте точкой.

6. На 21 карточке написаны числа 11,12,13,…,31 соответственно (по одному числу на карточке). Участники математического кружка Вася, Петя и Миша собрались разделить между собой все эти карточки так, чтобы каждому досталась хотя бы одна карточка и ни у кого не нашлось пары карточек, разность чисел на которых нечётна. Сколько существует способов такого дележа? Ответ дайте в виде целого числа.

7. Числа p и q подобраны так, что парабола y=qx−x2 пересекает гиперболу xy=p в трёх различных точках A,B и C, причём сумма квадратов сторон треугольника ABC равна 378, а точка пересечения его медиан находится на расстоянии 3 от начала координат. Найдите произведение pq. Ответ дайте в виде действительного числа, округлив его при необходимости стандартным образом до сотых. Целую и дробную части разделяйте точкой. Если возможных различных значений произведения pq окажется несколько, в ответе укажите их сумму.

8. Для всех троек (x,y,z), удовлетворяющих системе 2sinx=tgy, 2cosy=ctgz, sinz=tgx, найдите наименьшее значение выражения cosx−sinz. Ответ дайте в виде действительного числа, округлив его при необходимости стандартным образом до сотых. Целую и дробную части разделяйте точкой.

9. Сколько существует натуральных чисел n∈[20052019;20182004], для которых число [(3+17√2)n] нечётно?
(Здесь через [x] обозначено наибольшее целое число, не превосходящее x.) Ответ дайте в виде целого числа.

10. Найдите наименьшее из решений неравенства
(−log2(120−2x*sqrt(32−2x)^2+|log_2((120−2x2x*sqrt(32−2x))/(x^2-2x+8)^3))/(5log_7(71−2x*sqrt(32−2x))−2log_2(120−2x*sqrt(32−2x)))⩾0. Ответ дайте в виде действительного числа, округлив его при необходимости стандартным образом до сотых. Целую и дробную части разделяйте точкой. Если наименьшего решения не существует, в ответ запишите 0.

Источник

Найдите все такие что числа простые укажите сумму всех таких чисел

Загрузка решений доступна для зарегистрировавшихся пользователей

чисел () называются близкими, если каждое из них меньше, чем сумма всех чисел, деленная на Пусть . — n близких чисел, — их сумма.

а) все они положительны;

б) всегда

в) всегда

Загрузка решений доступна для зарегистрировавшихся пользователей

На доске написаны числа 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10, 1/11 и 1/12.

а) Докажите, что как бы мы ни расстaвляли знаки «+» и «−» между этими числами, выражение не будет равно 0.

б) Какое наименьшее количество написанных чисел необходимо стереть с доски для того, чтобы после некоторой расстановки «+» и «−» между оставшимися числами значение выражения равнялось 0?

Загрузка решений доступна для зарегистрировавшихся пользователей

Натуральные числа и получаются друг из друга перестановкой цифр. Докажите, что

а) суммы цифр чисел и равны;

б) если и чётные, то суммы цифр чисел и равны;

в) суммы цифр чисел и равны.

Загрузка решений доступна для зарегистрировавшихся пользователей

Для любого натурального числа через обозначим такое наибольшее натуральное число, что для любого натурального числа не превосходящего число представимо в виде суммы квадратов натуральных чисел.

а) Докажите для любого неравенство

б) Найдите хотя бы одно такое натуральное число что

в) Докажите, что существует бесконечно много таких натуральных что

Источник

ГОТОВИМСЯ К МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЕ ( СБОРНИК ЗАДАЧ С РЕШЕНИЯМИ И ОТВЕТАМИ ДЛЯ 8 КЛАССА)

ГОТОВИМСЯ К МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЕ

( СБОРНИК ЗАДАЧ С РЕШЕНИЯМИ И ОТВЕТАМИ ДЛЯ 8 КЛАССА)

Составитель : учитель математики высшей категории школы № 2036

Графики трёх функций y = ax+a, y = bx+b и y = cx+d имеют общую точку, причём a 6= b. Обязательно ли c = d? Ответ обоснуйте.

Ясно, что точка (–1, 0) принадлежит первым двум прямым. Так как a ≠ b , то эти прямые различны, значит, другой общей точки у них нет. Следовательно, точка (–1, 0) принадлежит и графику третьей функции, то есть 0 = – c + d .

Вершину A параллелограмма ABCD соединили отрезками с серединами сторон BC и CD.

Один из этих отрезков оказался вдвое длиннее другого. Определите, каким является угол BAD:

острым, прямым или тупым.

Первый вторник месяца Митя провёл в Смоленске, а первый вторник после первого понедельника — в Вологде. В следующем месяце Митя первый вторник провёл во Пскове, а первый вторник после первого понедельника — во Владимире. Сможете ли вы определить, какого числа и какого месяца Митя был в каждом из городов?

Решение: Поскольку Митя не мог провести один и тот же день и в Смоленске и в Вологде, значит, месяц начинался во вторник (ведь иначе первый вторник и первый вторник после первого понедельника совпали бы). Аналогично заключаем, что и второй месяц должен начинаться во вторник. Это возможно только в случае, когда один месяц — февраль, а другой — март, причём год не високосный. Отсюда уже легко получить, что в Смоленске Митя был 1 февраля, в Вологде — 8 февраля, во Пскове — 1 марта, во Владимире — 8 марта. Ответ : В Смоленске — 1 февраля, в Вологде — 8 февраля, в Пскове — 1 марта, во Владимире — 8 марта.

Эксперту предъявили 12 одинаковых на вид монет, среди которых, возможно, есть фальшивые. Все настоящие монеты весят одинаково, все фальшивые — тоже, фальшивая монета легче настоящей. У эксперта есть чашечные весы и эталонные монеты: 5 настоящих и 5 фальшивых. Сможет ли он за 4 взвешивания определить количество фальшивых монет среди предъявленных?

Решение. Очевидно, достаточно показать, что можно за два взвешивания определить количество фальшивых монет среди шести данных. Назовем эти шесть монет неизвестными . Берем три настоящие монеты и три фальшивые, взвешиваем их с неизвестными. Если весы в равновесии, то среди неизвестных монет ровно три фальшивых. Пусть вес эталонных монет больше. Тогда среди неизвестных монет 4, 5 или 6 фальшивых. Возьмём пять эталонных фальшивых и одну эталонную настоящую и взвесим их с неизвестными монетами. При равенстве мы получаем, что среди неизвестных монет ровно 5 фальшивых, если перевесят эталонные — 6 фальшивых, если перевесят неизвестные — 4 фальшивых. Случай, когда при первом взвешивании перевесили неизвестные монеты, рассматривается аналогично, но второе взвешивание производится с 5 эталонными настоящими монетами и одной эталонной фальшивой.

Взяли четыре натуральных числа. Для каждой пары этих чисел выписали их наибольший общий делитель. Получились шесть чисел: 1, 2, 3, 4, 5, N , где N > 5. Какое наименьшее значение может принимать число N ?

Решение . Число N может равняться 14, как показывает, например, четвёрка чисел 4, 15, 70, 84. Осталось показать, что N  14.

Лемма . Среди попарных НОД четырёх чисел не может быть ровно двух чисел, делящихся на некоторое натуральное k . Доказательство . Если среди исходных четырёх чисел есть не больше двух чисел, делящихся на k , то среди попарных НОД на k делится не более одного. Если же три из исходных чисел делятся на k , то все три их попарных НОД делятся на k .

Применяя лемму к k = 2, получаем, что число N чётно. Применяя её же к k = 3, k = 4 и k = 5, получаем, что N не делится на 3, 4 и 5. Значит, N не может равняться 6, 8, 10 и 12.

На стороне AC треугольника ABC выбрана точка D такая, что BD = AC. Медиана AM этого треугольника пересекает отрезок BD в точке K. Оказалось, что DK = DC. Докажите, что AM+KM = AB.

На окружности отметили 2013 точек и каждую соединили с двумя соседними. Также отметили центр окружности и соединили его со всеми остальными отмеченными точками. Можно ли покрасить 1007 отмеченных точек в красный, а остальные 1007 — в синий цвет так, чтобы каждая красная точка была соединена с нечётным числом синих, а каждая синяя — с чётным числом синих?

Дан выпуклый пятиугольник ABCDE, причём прямая BE параллельна прямой CD и отрезок BE короче отрезка CD . Внутри пятиугольника выбраны точки F и G таким образом, что ABCF и AGDE — параллелограммы. Докажите, что CD = BE + FG.

На клетчатой доске размером 20142014 закрашено несколько (не меньше одной) клеток так, что в каждом квадратике размером 33 клетки закрашено чётное число клеток. Каково наименьшее возможное число закрашенных клеток? (М. Антипов)

Оценка . Пусть на доске закрашено меньше 1342 клеток. Назовём тройку горизонталей доски, идущих подряд, слабой , если в ней есть хотя бы две горизонтали, не содержащие закрашенных клеток. Покажем, что слабые тройки есть . В самом деле, разобьём все горизонтали доски, кроме первой, на тройки идущих подряд. Получим 671 тройку. Если среди них нет слабых, то в каждой содержится не меньше двух закрашенных клеток, и всего закрашено не меньше, чем 6712 = 1342 клетки — противоречие.

Заметим, что найдётся слабая тройка, в которой есть закрашенные клетки . Действительно, возьмём произвольную слабую тройку. Если в ней нет закрашенных клеток, то, двигая её в сторону одной из закрашенных клеток, мы рано или поздно наткнёмся на строку, где закрашенные клетки есть, и получим искомую тройку. Зафиксируем её, удалим из прямоугольника 20143, составленного из её горизонталей, три крайние правые клетки, а оставшийся прямоугольник 20133 разобьём на 671 квадрат 33. В каждом из этих квадратов либо две закрашенных клетки, либо ни одной. Если в каждом по две, то всего закрашено не меньше 1342 клеток — противоречие. Значит, найдётся квадрат без закрашенных клеток. Будем двигать его по горизонтали в сторону ближайшей закрашенной клетки. Когда в него впервые попадёт закрашенная клетка, получим квадрат, в котором закрашена ровно одна клетка — противоречие

Дано 2014 попарно различных натуральных чисел таких, что произведение любых двух из них делится на сумму этих двух чисел. Докажите, что ни одно из данных чисел не может быть равно произведению шести попарно различных простых чисел.

Замечание. Числа 2014 не могло оказаться даже среди 15 выбранных. Чтобы убедиться в этом, достаточно заметить, что все делители вида 2014+ a больше 2014, а таких делителей у числа 2014 2 ровно (27–1)/2 = 13 14: все делители числа 2014 2 , кроме 2014, делятся на пары дополняющих друг друга до 2014 2 , и в каждой паре ровно один делитель больше 2014.

Найти двузначное число, зная, что число его единиц на 2 больше числа десятков и что произведение искомого числа на сумму его цифр равно 144.

Ученику надо было умножить 78 на двузначное число, в котором цифра десятков втрое больше цифры единиц; по ошибке он переставил цифры во втором сомножителе, отчего и получил произведение, на 2808 меньшее истинного. Чему равно истинное произведение?

Сумма цифр двузначного числа равна 12. Если к этому числу прибавить 36, то получится число, записанное теми же цифрами, но в обратном порядке. Найти искомое двузначное число.

Решение: Пусть x — цифра десятков, y — цифра единиц искомого числа. Тогда само число равно 10x+y. Из условия следует, что x+y=12 и 10x+y+36=10y+x. Получаем систему двух уравнений, которую можно решить методом подстановки: выразить из первого уравнения x и подставить во второе полученное выражение. В результате, x=4 и y=8. Ответ: 48

При каких натуральных n число m=3n2+5n+2 : 2n+3 также будет натуральным?

При каких натуральных n дробь 3n+5 : 5n+2 сократима?

Сумма квадратов крайних чисел четырехзначного числа M равна 58. Сумма квадратов средних цифр этого числа равна 68. Сумма числа M и числа 4536 равна числу, записанному теми же цифрами числа М, но в обратном порядке. Найдите число M.

Подберите такие не равные нулю числа n и m , чтобы равенство ( n · 5n ) n = m · 59 было верным.

Решение . Таких пар чисел бесконечно много.

Покажем, как можно получить другие решения. Возьмем произвольное n. Например, n = 6.

В подводном царстве живут осьминоги с семью и восемью ногами. Те, у кого 7 ног, всегда врут,

а те, у кого 8 ног, всегда говорят правду. Однажды между тремя осьминогами состоялся такой

Зеленый осьминог: «У нас вместе 24 ноги».

Синий осьминог: «Ты прав!»

Красный осьминог: «Глупости, Зелёный говорит ерунду!»

Сколько ног было у каждого осьминога? (Ответ обоснуйте.)

Ответ . У Зеленого осьминога 7 ног, у Синего осьминога 7 ног, у Красного осьминога 8 ног.

Решение Из условия задачи следует, что количество ног и правдивость высказываний связаны

однозначно. Синий и Красный осьминоги про слова Зеленого осьминога произнесли

противоречащие друг другу фразы. Значит, кто-то из них сказал правду, а кто-то ложь. А это, в

свою очередь, означает, что у кого-то из них 7 ног. Таким образом, слова Зеленого осьминога –

ложь (в противном случае у каждого из трех осьминогов должно быть по 8 ног, иначе общее

количество ног меньше 24). Подведем итоги: Зеленый осьминог сказал ложь, у него 7 ног; тогда

Синий осьминог сказал ложь, у него 7 ног, а Красный осьминог сказал правду, у него 8 ног.

Фирма изготавливает лимонный напиток, разбавляя лимонный сок водой. Сначала фирма

производила напиток, содержащий 15% лимонного сока. Через некоторое время генеральный директор отдал указание снизить содержание лимонного сока до 10%. На сколько процентов

увеличится количество производимого лимонного напитка при тех же объёмах поставок лимонов?

1 способ . Содержание лимонного сока в напитке после указания генерального директора

снизилось в полтора раза. Значит, из тех же лимонов можно приготовить в полтора раза больше

лимонного напитка. Иными словами, количество производимого лимонного напитка увеличится в

полтора раза или на 50%.

2 способ . Пусть х – количество производимого напитка до указания генерального директора. Тогда

количество лимонного сока в этом напитке – 0,15·х. Пусть теперь у – количество производимого

напитка после указания генерального директора. Тогда количество лимонного сока в этом напитке

– 0,1·у. Так как подразумевается, что количество лимонного сока не изменилось, получаем

равенство 0,15·х = 0,1·у. Умножив обе части этого равенства на 10, получим: у = 1,5·х; или: у = х +

0,5·х. Значит, количество производимого напитка увеличилось на 50%.

Все натуральные числа, сумма цифр в записи которых делится на 5, выписывают в порядке

возрастания: 5, 14, 19, 23, 28, 32, … Чему равна самая маленькая положительная разность между

соседними числами в этом ряду? Приведите пример и объясните, почему меньше быть не может.

Ответ . Наименьшая разность равна 1, например, между числами 49999 и 50000.

Решение Разность меньше 1 быть не может, так речь идет про разность различных натуральных

Понятно, что если два соседних числа отличаются только в разряде единиц, то разность между

ними равна 5 (например, 523 и 528). Значит, нужно, чтобы числа отличались и в других разрядах.

Можно попробовать взять большее число круглым, тогда числа будут отличаться минимум в двух

разрядах. Возьмем, например, 50, предыдущее число 46, а разность равна 4. Если взять 500, то

предыдущее число 497 и разность равна 3. Осталось подобрать такое число нулей, чтобы разность

На стандартном тетрадном листе в клетку нарисован угол (см. рисунок). Найдите его величину,

не используя измерительные инструменты. Ответ обоснуйте.

Решение . Соединим две «крайние» точки отрезком (как на

рисунке). Получившийся треугольник – равнобедренный, так как

две его стороны АВ и ВС являются диагоналями трёхклеточных

прямоугольников. Диагональ АВ делит угол прямоугольника с

вершиной В на два угла, дополняющих друг друга до прямого.

Треугольники ADB и CEB равны по двум катетам, значит, равны

их соответствующие углы. И значит, угол CBE дополняет угол

ABE до прямого. Таким образом, треугольник АВС –

равнобедренный и прямоугольный. Его углы А и С при основании

АС равны по свойству равнобедренного треугольника и имеют

величину 45° по теореме о сумме углов треугольника.

Комментарий . Если соединить точку В с серединой АС , мы также получим равнобедренный

прямоугольный треугольник. Рассуждения аналогичны.

На координатной плоскости есть точки, координаты ( x;y ) которых удовлетворяют уравнению

координаты ( x;y ) которых удовлетворяют этому уравнению.

Решение . Преобразуем уравнение следующим образом:

точки с координатами, удовлетворяющими уравнению,

представляют собой совокупность двух прямых: прямой,

параллельной оси ординат и проходящей через точку (-1;0) и

прямой, являющейся графиком функции у = х – 1 (см. рисунок).

Назовём хорошими прямоугольниками квадрат со стороной 2 и прямоугольник со сторонами 1 и 11. Докажите, что любой прямоугольник с целочисленными сторонами, большими 100, можно разрезать на хорошие прямоугольники.

В треугольнике ABC сторона AB больше стороны BC . На продолжении стороны BC за точку C отметили точку N так, что 2 BN = AB + BC . Пусть BS — биссектриса треугольника ABC , M — середина стороны AC , а L — такая точка на отрезке BS , что ML ∥ AB . Докажите, что 2 LN = AC .

Сумма квадратов n простых чисел, каждое из которых больше 5, делится на 6. Докажите что и n делится на 6.

Решение. Если сумма нескольких чисел делится на шесть, то и сумма их остатков при делении на шесть тоже будет делится на 6. Простое число, большее пяти, может иметь при делении на 6 только остатки 1 или 5 (иначе это число будет делиться на 2 или 3). Следовательно, квадрат любого простого числа, большего чем 5, имеет при делении на 6 остаток 1. Так как сумма этих остатков равна количеству чисел n, значит n делится на 6

Сумма квадратов n простых чисел, каждое из которых больше 5, делится на 6. Докажите что и n делится на 6.

Решение. Если сумма нескольких чисел делится на шесть, то и сумма их остатков при делении на шесть тоже будет делится на 6. Простое число, большее пяти, может иметь при делении на 6 только остатки 1 или 5 (иначе это число будет делиться на 2 или 3). Следовательно, квадрат любого простого числа, большего чем 5, имеет при делении на 6 остаток 1. Так как сумма этих остатков равна количеству чисел n, значит n делится на 6.

Петя и Вася сделали в тире по 5 выстрелов. Первыми тремя выстрелами они выбили поровну, а последними тремя Петя выбил в три раза больше очков, чем Вася. На мишени остались пробоины в 10, 9, 9, 8, 8, 5, 4, 4, 3, 2 очков. Куда попал каждый из них третьим выстрелом? Приведите все возможные варианты ответа и докажите, что других нет.

Если дату 10 февраля 2001 года записать в виде 10.02.2001, а затем убрать точки, то получится палиндром (т.е. число, читающееся слева направо и справа налево одинаково). Найдите ближайшую к 10.02.2001 дату, обладающую тем же свойством. Рассмотрите два случая:
1) требуемая дата еще не наступила,
2) требуемая дата уже прошла.
Ответ обосновать.

Ответ. 1) 20 февраля 2002 2) 29 ноября 1192 года.

Решение.
Заметим, что при условии, что дата записывается как палиндром, день и месяц однозначно находятся по заданному году.

пункт (1): в 2001 году других палиндромов быть не может, а в следующем (2002) году это должен быть 20 день второго месяца.

В выпуклом четырехугольнике ABCD стороны AB и CD параллельны, а диагонали AC и BD перпендикулярны. Докажите, что AD+BC = AB+CD.

Нарисуйте на плоскости пять различных прямых так, чтобы они пересекались ровно в семи различных точках.

Решение :
Три возможных ответа изображены на рисунке 1. Можно показать, что других конфигураций из пяти прямых, пересекающихся ровно в семи различных точках, нет.

Задача № 32 :

Мальчик пошел с отцом в тир. Отец купил ему 10 пулек. В дальнейшем отец за каждый промах отбирал у сына одну пульку, а за каждое попадание давал одну дополнительную пульку. Сын выстрелил 55 раз, после чего пульки у него кончились. Сколько раз он попал?

Решение :
Каждый раз, когда мальчик попадал в цель, число имеющихся у него пулек оставалось прежним (одну использовал и одну получил от отца). Каждый раз, когда мальчик промахивался, число имеющихся у него пулек уменьшалось на 2 (одну использовал и одну отобрал отец). Это значит, что сын за 55 выстрелов промахнулся 10 : 2 = 5 раз, стало быть, попал 55 – 5 = 50 раз.

Когда Винни-Пух пришел в гости к Кролику, он съел 3 тарелки меда, 4 тарелки сгущенки и 2 тарелки варенья, а после этого не смог выйти наружу из-за того, что сильно растолстел от такой еды. Но известно, что если бы он съел 2 тарелки меда, 3 тарелки сгущенки и 4 тарелки варенья или 4 тарелки меда, 2 тарелки сгущенки и 3 тарелки варенья, то спокойно смог бы покинуть нору гостеприимного Кролика. От чего больше толстеют: от варенья или от сгущенки?

Ответ : от сгущенки.

3м + 4с + 2в > 2м + 3с + 4в,

3м + 4с + 2в > 4м + 2с + 3в,

Складывая последнее неравенство с неравенством (*), получаем м + 3с > м + 3в, откуда с > в.

Два совершенно одинаковых катера,
имеющих одинаковую скорость в стоячей воде,
проходят по двум различным рекам одинаковое расстояние
(по течению) и возвращаются обратно (против течения).
В какой реке на эту поездку потребуется больше времени:
в реке с быстрым течением или
в реке с медленным течением?

Решение Пусть скорость катеров v км/ч,
скорость течения в первой реке v ₁ км/ч,
а скорость течения во второй реке v ₂ км/ч.
Пусть v ₁ >v ₂ .
Если обозначить расстояние, проходимое в одном направлении катерами, через S ,
то время, затраченное первым катером на весь путь,

а время, затраченное вторым катером,

Поскольку числители у обоих выражений одинаковы,
то большей будет дробь с меньшим знаменателем,
а так как знаменатели есть разности с равными уменьшаемыми,
то знаменатель меньше у первой дроби,
у которой вычитаемое v ₁ 2 больше.

Больше времени потребуется на поездку в реке с более быстрым течением.

Найти скорость и длину поезда,

если известно,
что он проходит мимо неподвижного наблюдателя в течение 7 с

и затратил 25 с,
чтобы проехать вдоль платформы длиной в 378 м.

Скорость можно определить сразу:
для проезда мимо платформы поезду потребовалось 25-7=18 (с).
Следовательно, его скорость
378:18=21 (м/с),
длина его 21· 7=147 (м).

В трех кучках лежат соответственно 12, 24 и 19 спичек. За ход можно переложить спичку из одной кучки в другую. За какое наименьшее число ходов можно получить три кучки с 8, 21 и 26 спичками?

Решение : Менее чем 4 ходами не обойтись: чтобы получить кучку из 8 спичек, придется из любой первоначальной кучки убрать как минимум 4 спички. Четырех ходов достаточно: перекладываем из кучки с 12 спичками по 2 спички в кучки с 19 и 24 спичками.

У даты 12.04.1961 (то есть 12 апреля 1961 года) сумма цифр равна 24. Найдите ближайшую дату после 01.01.2008, у которой сумма цифр равна: а) 35; б) 7.

Ответ : а) 29.09.2049; б) 03.01.2010.

Решение : а) Наибольшая сумма цифр числа равна 11 для 29-го числа. Наибольшая сумма цифр месяца равна 9 для сентября, то есть для 09. Значит, наибольшая сумма цифр в текущем году будет у даты 29.09.2008. Она равна 30, что меньше 35. Следовательно, надо менять и год. Последняя цифра года не более 9, и если мы сохраняем первые две цифры, то придется цифру десятилетий увеличить до 4.

б) Для 2008 года сумма цифр года уже больше 27, поэтому год придется изменить. Ближайший год в будущем с меньшей суммой цифр — 2010-й. Соответственно, ближайшая подходящая дата 03.01.2010.

Среди целых чисел от 8 до 17 включительно зачеркните как можно меньше чисел так, чтобы произведение оставшихся было точным квадратом. В ответе укажите сумму всех вычеркнутых чисел.

Решение : Чтобы произведение было точным квадратом, нужно, чтобы каждый простой множитель входил в него в четной степени. В произведение 8 · 9·. · 17 в нечетной степени входят 2, 7, 11, 13 и 17. Значит, мы обязаны вычеркнуть сомножители 11, 13 и 17. А вот чтобы «убить» лишние простые множители 2 и 7, хватит одного вычеркнутого сомножителя 14. Итого сумма вычеркнутых чисел равна 11 + 13 + 14 + 17 = 55.

На гранях кубика расставлены 6 различных чисел от 6 до 11. Кубик бросили два раза. В первый раз сумма чисел на четырех боковых гранях оказалась равна 36, во второй — 33. Какое число написано на грани, противоположной той, где написана цифра 10?

Решение : Cумма чисел на всех гранях равна 6 + 7 + 8 + 9 + 10 + 11 = 51. При первом броске сумма на верхней и нижней гранях равна 51 – 36 = 15, при втором — 51 – 33 = 18. Значит, на третьей паре противоположных граней сумма равна 51 – 15 – 18 = 18. Сумму 18 можно получить двумя способами: 11 + 7 или 10 + 8. Значит, на парах граней с суммой 18 напротив 11 находится 7, а напротив 10 — 8.

В конкурсе участвовали 5 человек. На каждый вопрос один из них дал неправильный ответ, остальные — правильный. Число правильных ответов у Пети равно 10 — меньше, чем у любого другого. Число правильных ответов у Васи равно 13 — больше, чем у любого другого. Сколько всего вопросов было в конкурсе?

Решение : Так как на каждый вопрос были даны 4 правильных ответа, общее число правильных ответов делится на 4. Поскольку Петя дал 10 верных ответов, Вася — 13, а остальные трое — от 11 до 12, то общее число правильных ответов не меньше, чем 10 + 13 + 3·11 = 56, и не больше, чем 10 + 13 + 3·12 = 59. Из чисел в этих пределах только 56 кратно 4, поэтому число вопросов равно 56: 4= 14

Команда из Пети, Васи и одноместного самоката участвует в гонке. Дистанция разделена на участки одинаковой длины, их количество равно 42, в начале каждого — контрольный пункт. Петя пробегает участок за 9 мин, Вася — за 11 мин, а на самокате любой из них проезжает участок за 3 мин. Стартуют они одновременно, а на финише учитывается время того, кто пришел последним. Ребята договорились, что один проезжает первую часть пути на самокате, остаток бегом, а другой — наоборот (самокат можно оставить на любом контрольном пункте). Сколько участков Петя должен проехать на самокате, чтобы команда показала наилучшее время?

Решение :Если Петя проедет 18 участков и пробежит оставшиеся 42 – 18 = 24, он затратит 18·3 + 24·9 = 270 мин. При этом Васе, наоборот, достанется проехать 24 участка, а пробежать 18, на что уйдет 24·3 + 18·11 = 270 мин — то же самое время. Если же Петя проедет меньшее число участков, то его время (и, соответственно, время команды) увеличится. Если Петя проедет большее количество участков, то увеличится время Васи (и время команды).

Достаточно обозначить число проезжаемых Петей участков через x и решить уравнение

Решить уравнение в целых числах:

(x – y)3 + (y – z)3 + (z – x)3 = 30

Решение: Преобразовав данное уравнение, получим:

3(x – y)(y – z)(z – x) = 30 или
(x – y)(y – z)(z – x) = 10.

Значит, целые числа
(x – y), (y – z), (z – x) — делители числа 10,
сумма этих делителей равна нулю.
Не трудно убедиться,
что таких делителей у числа 10 нет.

Вычислительное устройство вычитает из каждого трехзначного числа
сумму кубов его цифр.
Какое число нужно ввести в устройство,
чтобы результат оказался максимальным?

(100a + 10b + c) – (a3 + b3 + c3) = a(100 – a2) + b(10 – b2) + c(1 – c2).

Результат будет наибольшим
тогда и только тогда,
когда каждое слагаемое максимально,
то есть при
a = 6, b = 2, c = 0 или c = 1.

Задача № 44 :

График линейной функции отсекает от второй координатной четверти равнобедренный прямоугольный треугольник с длинами катетов, равными 3. Найдите эту функцию.

Решение :
Данный график образует с осью абсцисс такой же угол в 45, как и биссектриса первого и третьего координатных углов. Значит, ее угловой коэффициент равен 1. Поскольку при x = 0 значение функции равно 3, то искомая функция есть y = x + 3.

Банк ОГОГО меняет рубли на тугрики по 3000 рублей за тугрик, и еще берет 7000 рублей за право обмена независимо от меняемой суммы. Банк ЙОХОХО берет за тугрик 3020 рублей, а за право обмена берет 1 тугрик (тоже независимо от меняемой суммы). Турист установил, что ему все равно, в каком из банков менять деньги. Какую сумму он собираетс менять?

Решение : Если у туриста было X рублей, то в банке ОГОГО он получит за них (X – 7000) / 3000 тугриков, а в банке ЙОХОХО X / 3020 – 1 тугриков. Решая уравнение ( x – 7000 ) / 3000 = X / 3020 – 1, получаем X = 604000 (руб.).

Из чисел A, B и C одно положительно, одно отрицательно и одно равно 0. Известно, что A = B (B – C). Какое из чисел положительно, какое отрицательно и какое равно 0? Почему?

Последовательность строится по следующему закону.
На первом месте стоит число 7,
далее за каждым числом стоит сумма цифр его квадрата, увеличенная на 1.
Какое число стоит на 2000 месте?

Решение: Вычислим несколько первых членов последовательности:
7; 14; 17; 20; 5; 8; 11; 5; … — число 5 повторилось.
Значит, у последовательности есть период длины 3: числа 5; 8; 11 далее будут повторяться.
На пятом месте — пятерка, тогда для любого k > 0 на (3k + 2)-м месте также будет пятерка.

Так как 2000 = 3 x 666 + 2,
то 2000-м месте стоит число 5.

Решите в натуральных числах уравнение
zx + 1 = (z + 1) 2 .

Решение: При x = 1 или z = 1 уравнение решений не имеет.

Раскроем скобки и преобразуем равенство к виду z (zx–2 – 1) = 2.

Так как z и x не меньше 2, то левая часть уравнения неотрицательна.

При x = 2 корней нет.

Остается случай z = 2, тогда x = 3.

Из цифр 1, 2, 3, 4, 5, 6, 7
составляют всевозможные семизначные числа, в которых каждая цифра
участвует только один раз.
Доказать,
что сумма этих чисел делится на 9.

Решение: Сопоставим каждому такому числу x
число 8888888 – x,
оно также состоит из цифр 1, 2, 3, 4, 5, 6, 7
и каждая цифра используется один раз.

Сумма чисел в каждой паре 8888888.

Всего таких чисел 7!,
значит таких пар 7! / 2.
Значит вся сумма равна 7! х 4444444.

Число 7! делится на 9,

значит и сумма чисел делится на 9.

Ответ :Павел Петрович, Александр Павлович, Николай Павлович, Александр Николаевич, Александр Александрович, Николай Александрович.

Решение : В списке нет царя по имени Петр, следовательно, Павел Петрович был первый из этих царей. Других Павлов нет, следовательно, братья Александр Павлович и Николай Павлович правили сразу после Павла Петровича, сменив на троне один другого. Таким образом, последний царь был Николай Александрович (других Николаев нет). Александр Николаевич не мог править после последнего царя, значит, он унаследовал трон после Николая Павловича, который, следовательно, правил после своего брата Александра Павловича. Тогда наследником Александра Николаевича и отцом Николая Александровича мог быть только Александр Александрович.

. Дано трехзначное число ABB. Если перемножить его цифры, то получится двузначное число АС, а если перемножить цифры АС, то получится С. Найдите исходное число.

Решение. Так как А*С=С, то А=1 или С=0.

Первый случай: А=1. Тогда А*В*В=В2=1С, но есть только один квадрат между 10 и 20 – это 16, т.е. С=6. Откуда В=4. Т.е. исходное число 144: А=1, В=4, С=6.

Второй случай: С=0. Тогда А*В*В=А0=10А. Т.к. А – первая цифра, то А.0, можем сократить на А. Получим В2=10 – нет решения. Таким образом, ответ единственный.

Три математика ехали в разных вагонах одного поезда. Когда поезд подъезжал к станции, математики насчитали на перроне 7, 12 и 15 скамеек. Когда поезд отъезжал, каждый из них насчитал еще несколько скамеек, причем один из них насчитал в три раза больше, чем другой. А сколько насчитал третий?

Решение. Очевидно, что тот, кто до остановки проехал большую часть перрона, насчитал большее число скамеечек. Пусть первый насчитал 15 скамеек, второй 12, третий 7. Так как первый насчитал на 3 скамейки больше, чем второй, то, когда поезд будет отъезжать, второй увидит эти 3 скамейки, т.е. насчитает на 3 скамейки больше, чем первый. Аналогично третий насчитает на 8 скамеек больше, чем первый, и на 5 скамеек больше, чем второй. Раз кто-то насчитал в 3 раза больше, чем другой, то разница между насчитанными ими скамейками – четное

число (3x-x=2x). В нашем случае разность насчитанных скамеек четна только между первым и третьим и она равна 8. Значит, первый насчитал 8:2=4 скамейки, тогда второй 4+3=7 скамеек.

Замечание. Можно было обойтись и без четности. Пусть первый насчитал x скамеек. Тогда второй x+3, а третий x+8. А дальше составить всевозможные пары и решить получившиеся три уравнения (один насчитал в три раза больше, чем другой в паре): 3x=x+3, 3x=x+8, 3(x+5)=x+8. Только одно из них имеет целое решение.

Две машины едут по трассе скоростью 80 км/ч и с интервалом 10 м. У знака ограничения скорости машины мгновенно снижают скорость до 60 км/ч. С каким интервалом они будут двигаться после знака ограничения?

В шестизначном числе зачеркнули одну цифру и получили пятизначное. Из исходного числа вычли это пятизначное число и получили 654321. Найдите исходное число.

Источник