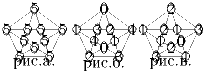
найдите все тройки натуральных чисел m n k такие что m3 n 3 k 32
Найдите все тройки натуральных чисел m n k такие что m3 n 3 k 32
Задача 1:
Найти все тройки ненулевых чисел a, b и c, образующих арифметическую прогрессию и таких, что из чисел 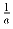
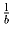
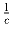
(Рекомендована жюри Российской олимпиады.)
Решение: По свойству арифметической прогрессии имеем a + c = 2b и одно из следующих уравнений
Первый случай приводит к уравнению b² = 2ac, которое не имеет решений при a + c = 2b; два других приводят к одному и тому же ответу: все тройки вида – 2t, – 0,5t, t, где t ≠ 0.
Ответ: – 2t, – 0,5t и t при t ≠ 0.
Задача 2:
Найдите тройки чисел a, b и c, являющиеся степенями пятёрки с целыми неотрицательными показателями, такие, что приписывая десятичную запись одного из них к десятичной записи другого, получим третье число.
(Рекомендована жюри Российской олимпиады.)
Задача 3:
В вершинах и точках пересечения диагоналей правильного пятиугольника записаны нули. За один ход разрешается добавить + 1 или – 1 одновременно ко всем числам, расположенным на какой-либо из диагоналей пятиугольника. Какие из указанных на рисунках пятиугольников можно получить через несколько ходов?
=0.5mm em:linewidth 0.4pt 0.4pt
Решение: Занумеруем диагонали пятиугольника числами от 1 до 5, и пусть x i – число добавленных единиц к i-ой диагонали. Число в любой вершине (точке пересечения диагоналей) равно сумме чисел x i по всем i таким, что i-ая диагональ проходит через эту вершину (точку пересечения диагоналей). Имеем систему десяти уравнений с пятью неизвестными, которая оказывается несовместной во всех изображённых на рисунках случаях.
Ответ: никакой пятиугольник получить нельзя.
Задача 4:
Найдите все тройки натуральных чисел m n k такие что m3 n 3 k 32
Задача C6
Для записи решений и ответов на задания С6 используйте бланк ответов № 2 .
Запишите сначала номер выполняемого задания С6 , а затем полное обоснованное решение и ответ.
Делители
05_P23 У натурального числа ровно 6 натуральных делителей. Сумма этих делителей равна 104. Найдите это число.
06_P24 У натурального числа ровно 9 натуральных делителей. Сумма этих делителей равна 741. Найдите это число.
07_P25 У натурального числа ровно 9 натуральных делителей Сумма этих делителей равна 1281. Найдите это число.
08_P26 натурального числа ровно 7 натуральных делителей. Сумма этих делителей равна 19531. Найдите это число
09_P27 У натурального числа ровно 6 натуральных делителей. Сумма этих делителей равна 1140. Найдите это число.
10_P28 Найдите наименьшее трехзначное натуральное число, квадрат которого при делении на 5 дает остаток 4.
Уравнения в целых числах
20_P12 Найдите все пары натуральных чисел k и n таких, что 

21_P16 Найдите все целые значения m и k такие, что 
22_P19 Найдите все натуральные числа, являющиеся степенью двойки, такие, что после зачеркивания первой цифры их десятичной записи снова получается десятичная запись числа, являющегося степенью двойки.
23_P18 Решите в натуральных числах уравнение 
Десятичная форма записи числа
24_P22 Два двузначных числа, записанных одно за другим, образуют четырёхзначное число, которое делится на их произведение. Найти эти числа.
Факториал
Сравнение чисел
36_P5 Сумма шестнадцати чисел равна 0.5. Оказалось, что сумма каждых пятнадцати из этих шестнадцати чисел положительна. Какое наименьшее целое значение может иметь наименьшее из данных чисел?
37_P6 Сумма восьми чисел равна 
40_P17 Среди обыкновенных дробей с положительными знаменателями, расположенных между числами 

Прогрессии и последовательности
41_P33 Какое наибольшее число членов может иметь геометрическая прогрессия, все члены которой – различно натуральные числа, большие 210 и меньшие 350?
42_P34 Какое наибольшее число членов может иметь геометрическая прогрессия, все члены которой – различно натуральные числа, большие 250 и меньшие 630?
43_D19 Каждое из чисел 2, 3, …, 7 умножают на каждое из чисел 13, 14, …, 21 и перед каждым из полученных произведений произвольным образом ставят знак плюс или минус, после чего все 54 полученных результата складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
45_D1 Перед каждым из чисел 2, 3, …, 6 и 10, 11, …, 20 произвольным образом ставят знак плюс или минус, после чего к каждому из образовавшихся чисел первого набора прибавляют каждое из образовавшихся чисел второго набора, а затем все 55 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
46_D8 Перед каждым из чисел 5, 6, …, 10 и 12, 13, …, 16 произвольным образом ставят знак плюс или минус, после чего к каждому из образовавшихся чисел первого набора прибавляют каждое из образовавшихся чисел второго набора, а затем все 30 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
47_D49 Гидролог вводит в компьютер измерения температуры забортнойводы. Температура измеряется с точностью до одной десятой градуса. За время наблюдений температура наблюдалась выше 10°C но ниже 17°C. Всего гидролог ввел 32 измерения, но из-за усталости, качки судна и плохой клавиатуры один раз вместо десятичной запятой гидролог нажал клавишу «0», а другой раз вообще не нажал десятичную запятую.
После упорядочивания данных получился ряд из 32 чисел, начинающийся числами 12,2; 12,8.
Если из полученного ряда удалить два первых числа, среднее арифметическое оставшихся равно 68,8. Если удалить два последних, то среднее арифметическое оставшихся равно 13,7. Определите, в каких числах и какие ошибки допустил гидролог.
48_D50 Метеоролог вводит в компьютер измерения температуры воздуха. Температура измеряется с точностью до одной десятой градуса. За все время наблюдений температура наблюдалась выше 20° но ниже 26°. Всего метеоролог ввел 22 измерения, но из-за усталости и плохой клавиатуры один раз вместо десятичной запятой метеоролог нажал клавишу «0», а другой раз вообще не нажал десятичную запятую.
После упорядочивания данных получился ряд из 22 чисел, начинающийся числами 21,3; 21,7.
Если из полученного ряда удалить два первых числа, среднее арифметическое оставшихся равно 149,53. Если удалить два последних, то среднее арифметическое оставшихся равно 23,28. Определите, в каких числах и какие ошибки допустил метеоролог.
Существуют ли такие натуральные числа m, n, k, что все три числа m^2+n+k, n^2+k+m, k^2+m+n являются квадратами натуральных
Ответ или решение 1
Нам заданы три натуральных числа m, n, и k.
Нужно ответить на вопрос: являются ли числа, заданные выражениями:
квадратами натуральных чисел?
Решать задачу будем используя алгоритм:
Допустим, что утверждение верно
Предположим что существуют такие m, n и k, для которых выполняются условия заданные в задаче, что m^2 + n + k; n^2 + k + m; k^2 + m + n являются квадратами натуральных чисел.
Вспомним определение натурального числа.
Множество натуральных чисел принято обозначать символом N.
Запишем утверждения, которые должны выполняться
Если выражение m^2 + n + k является квадратом натурального числа, то должно выполнятся неравенство:
m^2 + n + k > (m + 1)^2 (квадрат натурального числа должен быть больше квадрата следующего за ним натурального числа).
m^2 + n + k > m^2 + 2m + 1;
Аналогичное неравенство получаем и для двух других выражений:
n^2 + k + m > n^2 + 2n + 1;
И последнее неравенство:
k^2 + n + m > k^2 + 2k + 1;
Приходим к противоречию
Теперь сложим все три полученные неравенства:
2n + 2k + 2m > 2n + 2k + 2m + 3;
2(n + k + m) > 2(n + k + m) + 3.
В результате мы получили не верное неравенство.
Вывод: натуральных чисел, которые бы удовлетворяли заданным условиям не существует.
Найдите все тройки натуральных чисел m n k такие что m3 n 3 k 32
Приведём решение на языке Pascal.
В результате работы программа должна вывести следующее:
Приведем программу на языке Pascal, реализующую этот способ.
Приведем математическое обоснование данного способа.
Пусть разложение числа m на простые множители имеет вид тогда количество делителей числа m равно
В частности, четное число раскладывается на множители как
где множители ai — нечетные числа. Тогда число имеет
четных делителей и
нечетных.
Приведем решение Антона Борисова.
Заметим, что числа m и n не превышают 30, поскольку 2 30 > 1 000 000 000. Будем перебирать числа от 0 до 30, перемножать соответствующие степени двоек и троек и проверять, попало ли произведение в заданный диапазон. Для возведения числа в произвольную степень использована функция exp.
Найдите все тройки натуральных чисел m n k такие что m3 n 3 k 32
Приведём решение на языке Pascal.
arr2: array[1..30] of int64;
arr3: array[1..20] of int64;
answer: array[1..100] of int64;
for i := 1 to 100 do answer[i] := 0;
for i := 1 to 29 do arr2[i+1] := arr2[i] * 2 * 2;
for i := 1 to 19 do arr3[i+1] := arr3[i] * 3 * 3;
for j := 1 to 20 do begin
if ((arr2[i] * arr3[j]) >= 400000000) and ((arr2[i] * arr3[j]) answer[j] then begin
for k := 1 to 100 do
if answer[k] <> 0 then writeln(answer[k]);
В результате работы программа должна вывести следующее:
Приведем программу на языке Pascal, реализующую этот способ.
Приведем математическое обоснование данного способа.
Пусть разложение числа m на простые множители имеет вид тогда количество делителей числа m равно
В частности, четное число раскладывается на множители как
где множители ai — нечетные числа. Тогда число имеет
четных делителей и
нечетных.
Приведем решение Миша Бурмистрова.
Будем делить каждое число из заданного диапазона на 2 до тех пор, пока это возможно, а затем на 3. Таким образом мы определим значения переменных m и n. Если m — четное, n — нечетное, а результат деления равен 1, то число выводится на экран.