Вторая кинематическая теорема гельмгольца гласит что
Большая Энциклопедия Нефти и Газа
Теоремы Гельмгольца ( Helmholtz), касающиеся важных соотношений, которые наблюдаются при движении идеальной жидкости с вращением частиц, выведены им на основе электродинамических представлений. Однако следствия из этих теорем могут быть легко доказаны при рассмотрении вихревого шнура в потенциальном потоке. Потенциальное движение с циркуляцией, как показано выше, является многосвязной областью, где циркуляция одинакова вдоль всех кривых, если их можно перевести друг в друга, ае пересекая границ области. Из этого свойства следует, во-первых, что циркуляция вокруг вихревого шнура в одно и то же время во всех точках должна быть одинаковой и, во-вторых, что вихревой шнур должен либо представлять замкнутую кривую, либо достигать своими концами границ жидкости. [1]
Теоремы Гельмгольца ( Helmholtz), касающиеся важных соотношений, которые наблюдаются при движении идеальной жидкости с вращением частиц, выведены им на основе электродинамических представлений. Однако следствия из этих теорем могут быть легко доказаны при рассмотрении вихревого шнура в потенциальном потоке. Потенциальное движение с циркуляцией, как показано выше, является многосвязной областью, где циркуляция одинакова вдоль всех кривых, если их можно перевести друг в друга, не пересекая границ области. Из этого свойства следует, во-первых, что циркуляция вокруг вихревого шнура в одно и то же время во всех точках должна быть одинаковой и, во-вторых, что вихревой шнур должен либо представлять замкнутую кривую, либо достигать своими концами границ жидкости. [2]
Теорема Гельмгольца : Течение несжимаемой вязкой жидкости, удовлетворяющее условию (75.1), характеризуется тем свойством, что для этого течения диссипация энергии в любой области меньше диссипации энергии для любого другого течения с тем же распределением скорости v на границе. [3]
Теоремы Гельмгольца о вихревом движении основываются на теоремах Стокса и Томсона и устанавливают условия сохраняемости вихревого движения в идеальной жидкости. [4]
Вторая теорема Гельмгольца представляет чисто кинематическую теорему, не связанную со специфическими свойствами жидкостей или особенностями принятых их моделей. [5]
Из теоремы Гельмгольца вытекают важные для практических приложений следствия. [6]
Вторая теорема Гельмгольца представляет чисто кинематическую теорему, не связанную со специфическими свойствами жидкостей или особенностями принятых их моделей. [7]
Из теоремы Гельмгольца следует, что полная производная от обтечения по замкнутой жидкой линии равна нулю. Понятно, наоборот, что эта последняя теорема заключает в себе теорему Гельмгольца; дадим для нее самостоятельное доказательство. [8]
Вторая теорема Гельмгольца устанавливает, таким образом. [10]
Из теорем Гельмгольца вытекает, что образование вихревых линий и трубок в жидкости возможно только в случае, если плотность р не является функцией давления или внешние силы не имеют потенциала. [12]
Докажем теорему Гельмгольца : поток вихрей через поперечное сечение вихревой трубки в данный момент времени постоянен по ее длине. [13]
Рассмотрим теорему Гельмгольца о вихрях. [15]
Теоремы разложения Гельмгольца (о полноте сферических функций)
Теоремы разложения Гельмгольца
Если сила имеет потенциал, а плотность является функцией давления, то прочность вихревых линий и вихревых труб имеет сохраняемость. На основании полученных результатов получено доказательство этих теорем гидромеханики. Фактически, предположение, что уравнение Гельмгольца выполняется, короче говоря. То есть, при необходимости, как вихревые линии, так и прочность вихревой трубы являются.
В частности, если в первый момент нет вихря, то в последующие моменты вихря не будет. Таким образом, движение, которое не было вращательным в какой-то момент, всегда будет оставаться не вращательным, а движение, которое является вихревым уравнением в какой-то момент, всегда будет поддерживаться! Вихревой. Поэтому четко различают все движения до классов уравнения Фридмана Гельмгольца. То есть движение без вихря, или с потенциалом скорости, и движение вихря.
Любое векторное поле, однозначное, непрерывное и ограниченное во всем пространстве, может быть разложено на сумму потенциального и соленоидального векторных полей. Людмила Фирмаль
Если допущения, сделанные по теореме Гельмгольца, не будут выполнены, то теорема Гельмгольца перестанет выполняться, что позволит возникновение и разрушение вихрей. Поэтому под влиянием греха может возникнуть вихрь или схлопнуться основная причина: при отсутствии потенциала в силе, действующей на единицу массы жидкости. Если плотность зависит от других факторов, таких как температура, а не только от давления. Наконец, если жидкость не полная, пока всегда предполагается, но вязкая.
Скалярная функция называется скалярным потенциалом, векторная функция называется векторным потенциалом. Людмила Фирмаль
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Формулы Коши — Гельмгольца
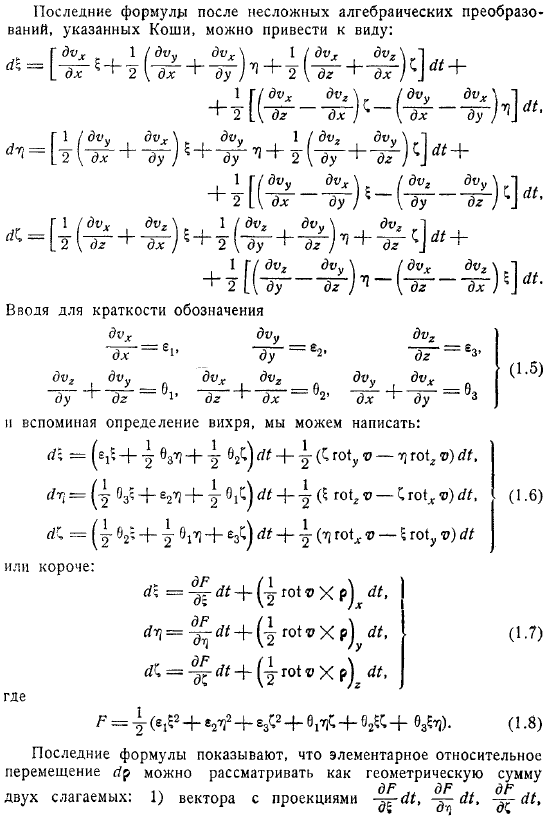
Теорема и Формулы Коши — Гельмгольца
Геометрические отношения
Таковым образом при этом протяженность остается постоянной во время перемещения условию твердости безусловный отрицательный радиус-вектор взят, а радиус гидромеханики образец вектор, отчерченный из некой зафиксированной в месте прикрепления точки, принимаемой им за неподвижную, то формула не просчитывает сразу деление простого перемещения и делит на поступательную и доли.
Обращаясь к исследованию движений и безразмерной и разных передвигающейся в масштабной среде, вырежем в ней в мыслях маленькую квадратичную функцию, ограниченную односвязной поверхностью, к примеру шаровидный круг, и осмотрим 3 поочередных расположения данной в факторе = нескончаемо небольшим интервалом проходящей вдоль линий пунктирной лини.
Подумаем и запишем в виде числа Х расположения двух всевозможных кривых и одну из их, к примеру примем из-за главную. и обозначим через их безусловные радиусы-векторы, проведенные из некие места через круг и обозначим прикреплённый радиус-вектор. Величины в другом расположении будущей формулы включённые в эпизод будто простые движения станут положительными числами.
| Формула | Радиус |
| Gs+Qe | 45 r |
Краткие обозначения
рассматривая полученные результаты и всё решение, будто простое смещение тонкой шаровидной формы разрешено пренебрегать как геометрической необходимой суммой четырёх движений, и деформационного размерного шва; разделив на два числа.
Мы можем подтвердить наиболее положительные позиции этого расчёта. В каком месте — о перемещении бывшей (характеризуемой неким предметом условным радиусом-вектором Р) кругом моментальной закреплённой оси, не проходящей чрез с круговой центр деформации.
Возможно только формула квадратичной однородной функции в которой коэффициенты имеют вышеуказанное смысл сможет помочь при дальнейших расчётах.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Теоремы о вихрях Гельмгольца
Даже если предпосылки законов вихря в реальных потоках лишь приблизительны, они объясняют
Содержание
требования
Плотность вихрей или вектор вихря является центральной переменной в теоретическом описании вихрей.
Вихревая линия является аналогом тока с использованием дифференциального уравнения Икс → ω ( s ) <\ displaystyle <\ vec 
Первый закон вихря Гельмгольца
Первая теорема Гельмгольца о вихрях утверждает, что области, свободные от вихрей, остаются свободными от вихрей в идеальных жидкостях.
Для доказательства кривая, охватывающая (бесконечно малую) небольшую площадь a, помещается вокруг неподвижного элемента жидкости. Из-за небольшого размера можно предположить, что плотность вихрей, которая постоянна по площади и исчезает согласно предположению, интеграл площади которой представляет собой интенсивность вихревой трубки с площадью поперечного сечения a, и эта интенсивность также исчезает согласно предположению. Согласно закону вихрей Кельвина, интенсивность является величиной сохранения, так что плотность вихрей постоянно исчезает в области a и, следовательно, также для рассматриваемого жидкого элемента.
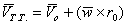. Для жидкой частицы основная теорема кинематики гласит, что скорость движения любой точки жидкой частицы складывается из скорости квазитвердого движения и деформационного. Квазитвердое состоит из поступательного вращательного: 
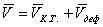. Для доказательства рассмотрим движение точки М с координатами x, y, z, которая находится в окрестности точки М0 (x0, y0, z0) и составляющая для точки М0 скорости (u0, υ0, w0), тогда раскладывая функцию скорости в ряд Тейлора и сохраняя компоненты первого порядка малости, составляющие скорости для точки М можно записать:
; 
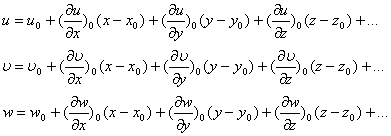
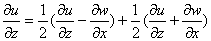
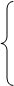
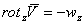
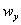
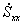
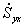
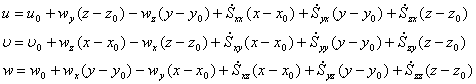
, входящие в скорость деформации, могут быть представлены в виде матрицы, которая называется тензором скоростей деформации:
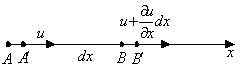
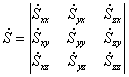
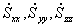— диагональные компоненты.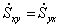
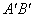. Произошла линейная деформация отрезка АВ на величину: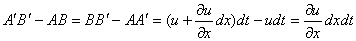
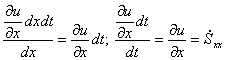
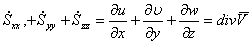
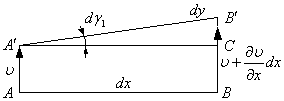
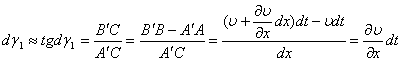
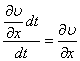
— скорость скашивания в направлении оси х.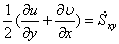 
— средняя скорость угловой деформации в плоскости ху.