Вычисли чему равно выражение arccos0
arccos 0 найти
Добрый день. Подскажите мне пожалуйста, чему будет равен arccos 0. Я вообще не понимаю, что от меня хотят, чтоб я сделала. Либо задание странно сформулировано, либо я что-то не усвоила. Надеюсь, что вы сможете мне помочь, а то самостоятельно у меня не получается. Заранее спасибо
Добрый вечер!
Спасибо за обращение. Ваш вопрос — не очень сложен и, скорее всего, Ваше непонимание появилось только из-за того, что Вы не совсем понимаете что значит arсcos, уже не говоря о более конкретном задании arсcos 0.
Давайте попробуем разобраться, что же это такое и с чем его едят.
Первым делом давайте уточним, что таких непонятных, на первый взгляд, обозначений существует несколько (это обратные тригонометрические функции): арксинус, арккосинус, арктангенс, арккотангенс. Это очень простые понятия. Которые могут облегчить человеку жизнь при решении тригонометрических уравнений!
Для понимания конкретно этих обозначений Вам нужно будет вспомнить, что такое синус, косинус, тангенс и котангенс. А также их табличные значения для некоторых углов. И тогда Вы полностью усвоите эту тему.
Итак: арксинус, арккосинус, арктангенс и арккотангенс — это просто какие-то углы. Ни больше ни меньше. Вы знаете угол 45 градусов. А бывает угол arcsin 0,4, или arctg(-1,3). дело в том, что углы можно просто напросто записать разными способами. Можно записать угол через градусы, а можно и через его синус, косинус, тангенс и котангенс.
Давайте расшифруем Ваш пример:
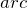

То есть получаем, что:
А теперь давайте подумаем, какой угол скрывается под таким обозначением, как
Для того, чтоб понять это не нужно придумывать велосипед. Достаточно просто вспомнить таблицу и мы с Вами получим следующее:
Другими словами, если расшифруем все возможные варианты, то получим такое:
То есть, ответ:
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Для четкого понимания рассмотрим пример.
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Таблица синусов основных углов предлагает такие результаты значений углов:
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
Следуя из таблицы, находим значения арккосинуса:
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | — 3 | — 1 | — 3 3 | 0 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c t g a к а к ч и с л о | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 | |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Нахождение значения arcsin, arccos, arctg и arcctg
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Арккосинус. Решение уравнения cos x=a
п.1. Понятие арккосинуса
\(arccos\frac12=\frac\pi3,\ \ arccos\left(-\frac<\sqrt<3>><2>\right)=\frac<5\pi><6>\)
\(arccos2\) – не существует, т.к. 2> 1
п.2. График и свойства функции y=arccosx
п.3. Уравнение cosx=a
 | Значениями арккосинуса могут быть только углы от 0 до π (180°). А как выразить другие углы через арккосинус? |
Углы в нижней части числовой окружности записывают через отрицательный арккосинус. А углы, которые превышают π по модулю, записывают через сумму арккосинуса и величины, которая ‘не помещается» в область значений арккосинуса.
Заметим, что полученный ответ является записью вида
\(x=\pm arccos\frac12+2\pi k\)
А т.к. арккосинус для \(\frac12\) точно известен и равен \(\frac\pi3\), то мы его и пишем в ответе.
Но так бывает далеко не всегда.
2) Решим уравнение \(cosx=0,8\)
 | Найдем точку 0,8 в числовой окружности на оси косинусов (ось OX). Построим вертикаль – перпендикуляр, проходящий через точку. Он пересечёт числовую окружность в двух точках. По определению верхняя точка – это угол, равный arccos0,8. Тогда нижняя точка – это тот же угол, но отложенный в отрицательном направлении обхода числовой окружности, т.е. (–arccos0,8). Добавление или вычитание полных оборотов к каждому из решений даст другие корни. Получаем ответ: \(x=\pm arccos0,8+2\pi k\) |
п.4. Формула арккосинуса отрицательного аргумента
Докажем полезную на практике формулу для \(arccos(-a)\).
п.5. Примеры
Пример 1. Найдите функцию, обратную арккосинусу. Постройте графики арккосинуса и найденной функции в одной системе координат.
Для \(y=arccosx\) область определения \(-1\leq x\leq 1\), область значений \(0\leq y\leq \pi\).
Обратная функция \(y=cosx\) должна иметь ограниченную область определения \(0\leq x\leq \pi\) и область значений \(-1\leq y\leq 1\).
Строим графики:
Графики симметричны относительно прямой y=x.
Обратная функция найдена верно.
Пример 2. Решите уравнения:
a) \(cos x=-1\) \(x=\pi+2\pi k\) | б) \(cos x=\frac<\sqrt<2>><2>\) \(x=\pm\frac\pi4+2\pi k\) |
в) \(cos x=0\) \(x=\pm\frac\pi2+2\pi k=\frac\pi2+\pi k\) | г) \(cos x=\sqrt<2>\) \(\sqrt<2>\gt 1,\ \ x\in\varnothing\) Решений нет |
д) \(cos x=0,7\) \(x=\pm arccos(0,7)+2\pi k\) | e) \(cos x=-0,2\) \(x=\pm arccos(-0,2)+2\pi k\) |
 | Способ 1. Решение с помощью числовой окружности |
Пример 4*. Решите уравнения:
\(a)\ arccos(x^2-3x+3)=0\) \begin
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Арккосинус
Напомним, что на единичной окружности косинус угла – это координата х точки А, соответствующей этому углу:
Задание. Решите ур-ние
Задание. Запишите корни ур-ния
Теперь будем подставлять в это решение значения n, чтобы найти конкретные значения х. Нас интересуют корни, которые больше π, но меньше 4π, поэтому будем сразу сравнивать полученные результаты с этими числами.
Получили два корня, относящихся к промежутку – это 7π/3 и 8π/3. Нет смысла проверять другие возможные значения n, ведь они будут давать корни, заведомо меньшие 2π/3 или большие 13π/3:
Как и в случае с косинусом, есть несколько частных случаев, когда решение ур-ния записывается проще. Ур-ние
Это видно из графика, где корням ур-ния соответствуют точки пересечения синусоиды с осью Ох:
Наконец, решениями ур-ния
Решение уравнений tgx = a и ctgx = a
Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):
Таким образом, у ур-ния tgx = a существует очевидное решение
Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:
Задание. Решите ур-ние
Задание. Запишите формулу корней ур-ния
Далее рассмотрим ур-ние вида
Задание. Решите ур-ние
Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии
Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.
Вычисли чему равно выражение arccos0
Арккосинус в переводе с латинского означает дуга и косинус. Это обратная функция.
Арккосинус числа а – это такое число в отрезке от 0 до π, косинус которого равен а.
При этом | a | ≤ 1.
Обозначается так: arccos a.
arccos a = t.
Следовательно, cos t = a.
Условия: модуль а не больше 1; t не меньше 0, но не больше π
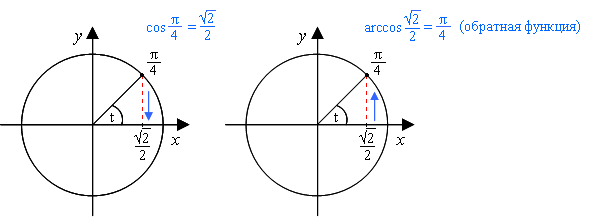
Пример-пояснение : Найдем arccos √2/2 (см.рисунок).
Выражение arccos √2/2 показывает, что косинус угла t равен √2/2 (cos t = √2/2).
Далее просто находим точку этого косинуса на числовой окружности, что и является ответом:
число √2/2, являющееся значением оси х, соответствует точке π/4 на числовой окружности.
Значит, arccos √2/2 = π/4.
если cos π/4 = √2/2, то arccos √2/2 = π/4.
То есть в первом случае по точке на числовой окружности определяем значение косинуса, а во втором – наоборот, по значению косинуса находим точку на числовой окружности. Движение в обратную сторону. Это и есть арккосинус.
Обобщим: косинус – это точка на оси х, а арккосинус – это соответствующая ей точка на окружности.
Формулы:
t = ± arccos a + 2πk, где k – любое целое число
arccos (-a) = π – arccos a, где 0 ≤ a ≤ 1
Пример 1 : Вычислить арккосинус 1/2.
Итак, а = 1/2. Значит, наша формула arccos a = t обретает конкретику:
Это означает, что косинус угла t равен 1/2:
При этом наша точка t находится на отрезке [0; π].
Находим значение t. Для этого смотрим на числовую окружность. Мы видим, что число 1/2 является абсциссой точки π/3 – то есть является косинусом угла π/3. Иначе говоря:
Подставляем значение t в выражение cos t = 1/2:
cos π/3 = 1/2. При этом π/3 входит в отрезок [0; π].
Совершаем обратное действие: если cos π/3 = 1/2, то:
Без объяснений процесс решения будет таким:
Обратите внимание: косинусом π/3 является 1/2, а арккосинусом 1/2 является π/3. Движение в обратную сторону. Косинусом числа является точка на оси координат, а арккосинусом – точка на числовой окружности.
√3
Пример 2 : Найти arccos – ——
2
√3
cos t = – ——, t ∈ [0; π]
2
√3 5π
arccos – —— = ——
2 6